目录

题目：

示例：

分析：

代码：

---

题目：

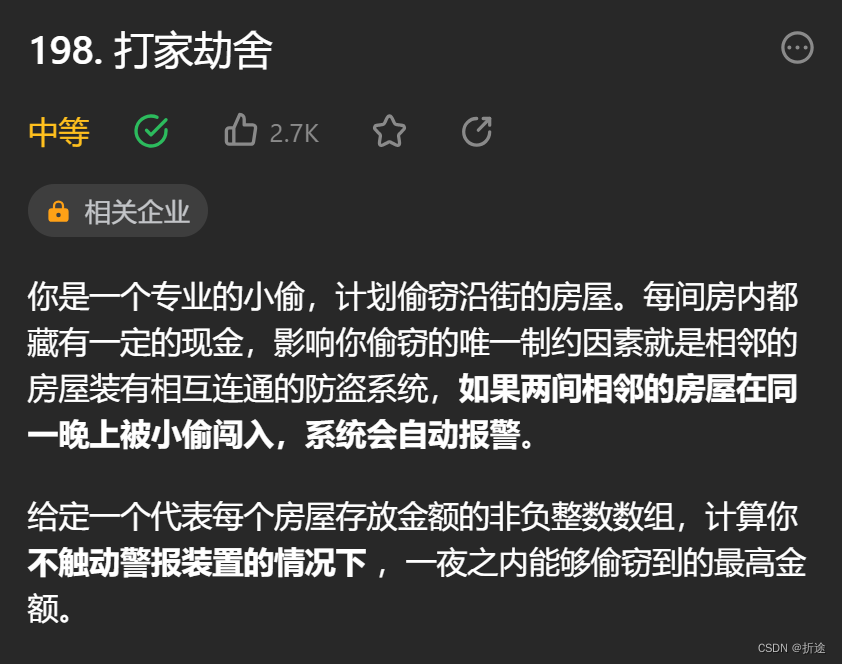
示例：

分析：

这是力扣里一道关于动态规划的很经典的一道题。

那么首先呢我们扮演一个小偷，有一堆的房屋让我们偷，但是我们不能偷相邻的房屋，问我们最终能偷多少。

那这道题我们能不能拆分成小问题呢。

答案当然是可以，如果我只有一间屋子能偷，那我能偷的最多的金额是不是就是这间屋子。
如果有两件屋子可以偷，不过由于限制不能偷相邻的屋子，所以我能偷的最多的金额是两间屋子的最大值。

如果有三间屋子，那么可以开始操作了，那我就可以选择偷或者是不偷第三间屋子了，如果偷，那么我就不能偷第二间屋子，我能偷的金额就是只有一间屋子的时候能偷的金额再加上第三间屋子的金额。

如果不偷，那么我能获取的最多的金额就是只有两间屋子的时候能获取的最多的金额。
发现规律了吗，我在n间屋子的情况下能获取的最多的金额，只和在n–1间屋子的情况下以及在n–2间屋子的情况下有关。

那么我们就找到了刚刚说的递推公式。
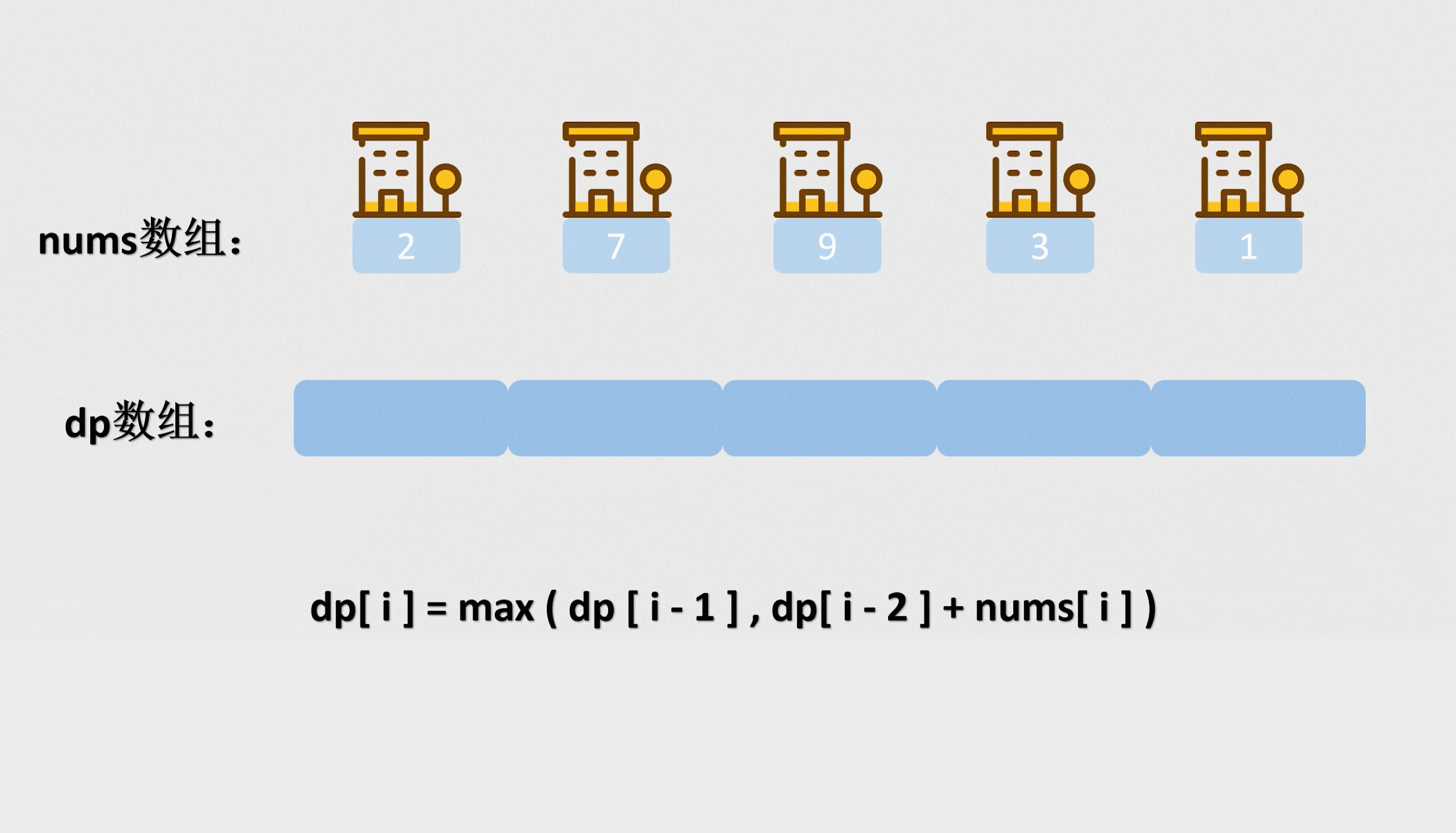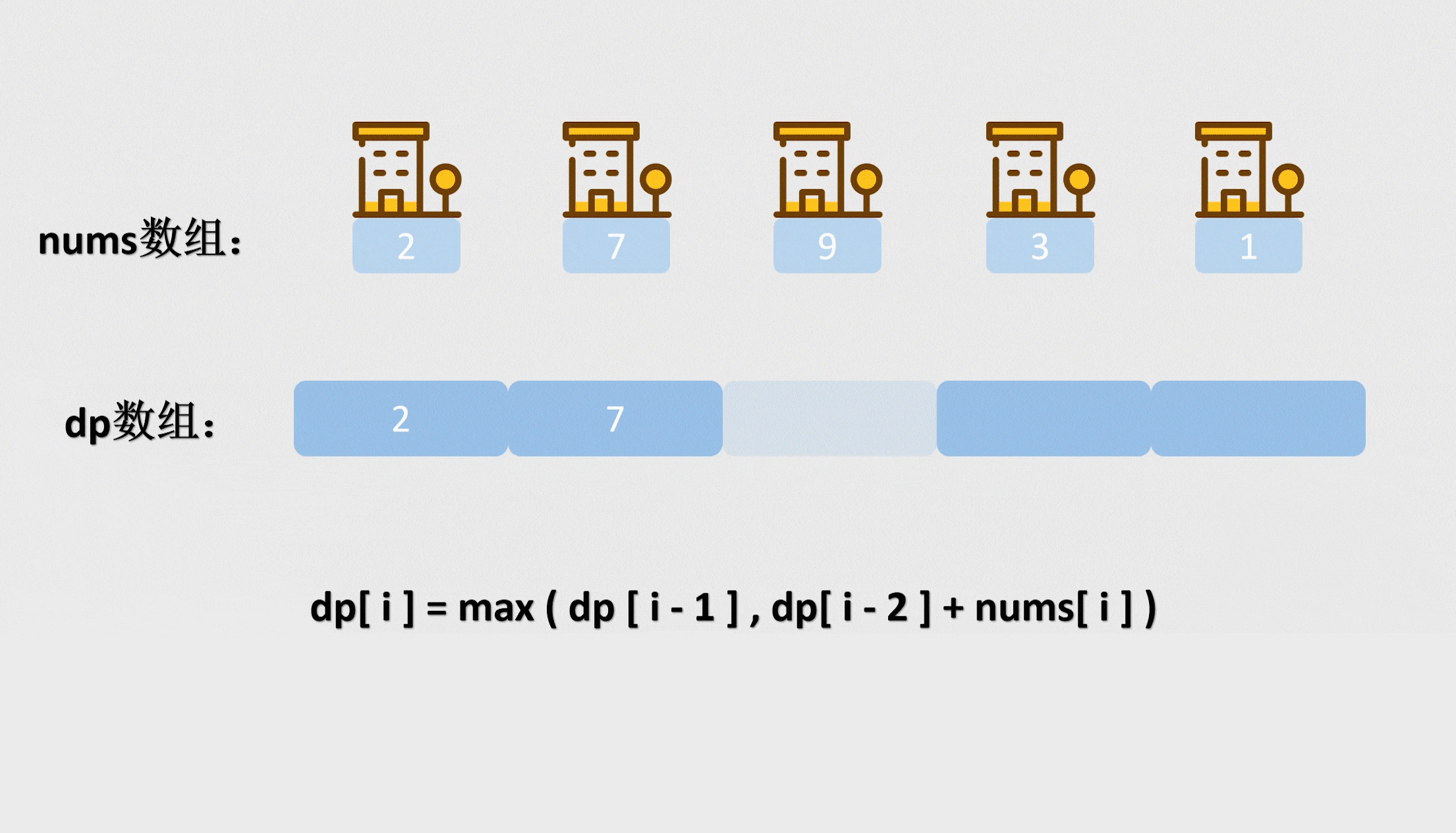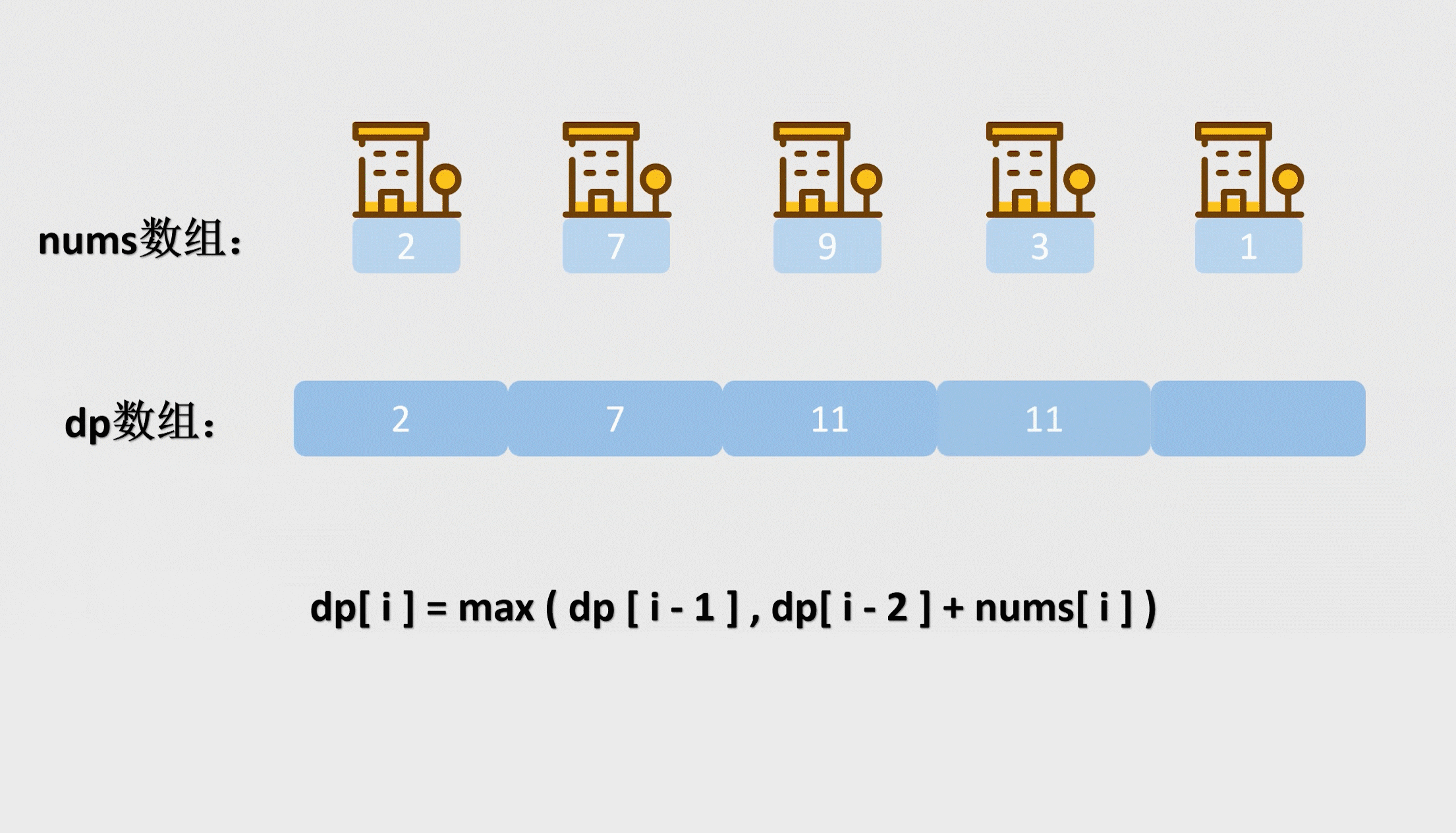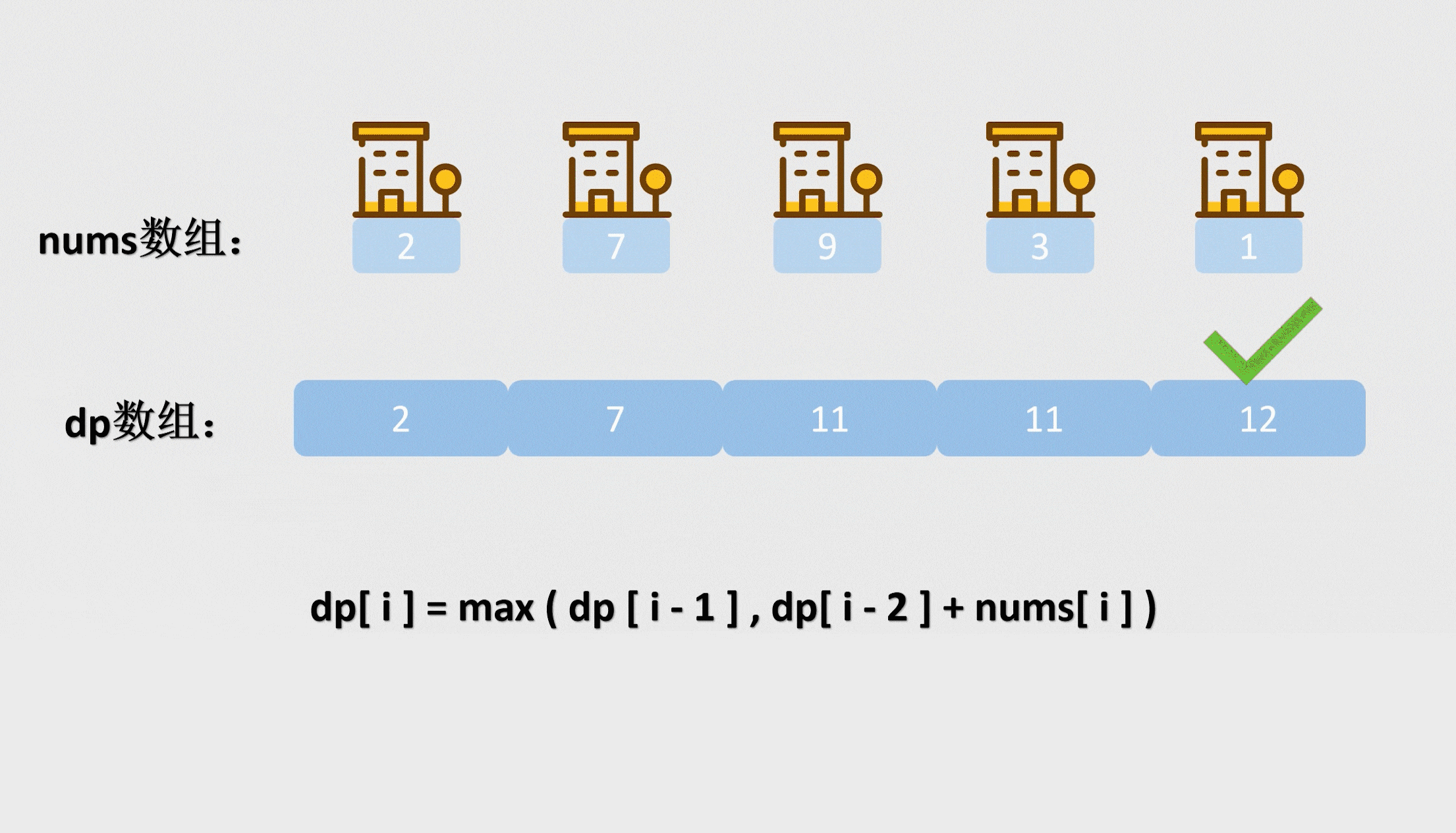
那递推公式就是这个

这个nums自然就是表示房屋价值的数组了。

而这个dp数组是什么意思，dp的第i–1个数表示的就是如果只有i间房子，我们能获取的最多的金额。dp数组就是存放我们这些小问题的状态的，由较前面的元素可以推断出后面元素的结果，这就是动态规划。

至于为什么叫dp数组呢，我也不知道，大家都管动态规划的状态数组叫dp，我也就跟着叫了。
我们要明确的点是dp里的元素是什么意思，下标为i–1的元素就是表示只有i间房子的情况下我们能获取的最多的数。

那dp数组的最后一个元素就是我们要返回出去的元素了。只不过我们现在还要一步步根据递推公式推导。

我们看这个递推公式，含义就是有i间房屋的情况下，我能获取的最多金额等于 在有i–1间房屋的情况下能获取到的最大金额 和 在有i–2间房屋的情况下能获取到的最大金额再加上第i间房屋的金额 的最大值。

 那么我们初始化前两间屋子之后，我们就可以用递推公式把整个dp数组填满了，最终返回dp的最后一个元素即可。

代码：

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()<2) return nums[0];   //如果数组长度就是等于1,那么直接返回这个元素即可
        
        vector<int>dp(nums.size(),nums[0]);
        dp[1]=max(nums[0],nums[1]);
        for(int i=2;i<nums.size();i++){
            dp[i]=max(dp[i-1],dp[i-2]+nums[i]); //偷本间屋子就不能偷上一间屋子,不偷本间屋子,那么获取的现金就跟上间屋子一样.
        }
        return *(dp.end()-1);
    }
};