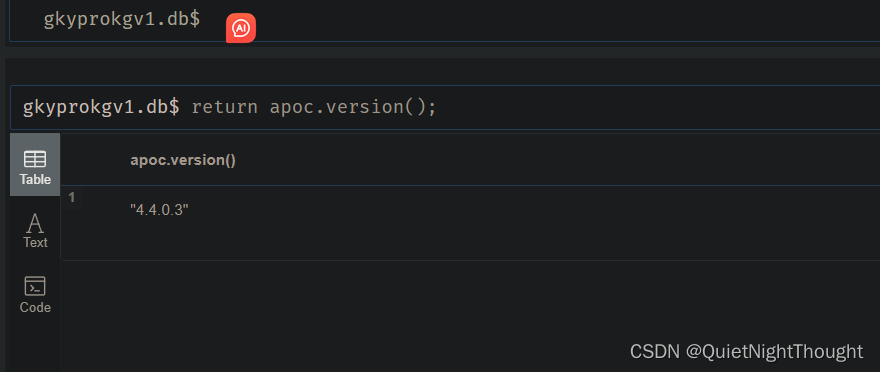
连续产量古诺模型

连续产量古诺模型是博弈论中非常经典的模型，以两厂商连续产量古诺博弈为例：

1、模型建立

Player：两个供应相同产品的厂商

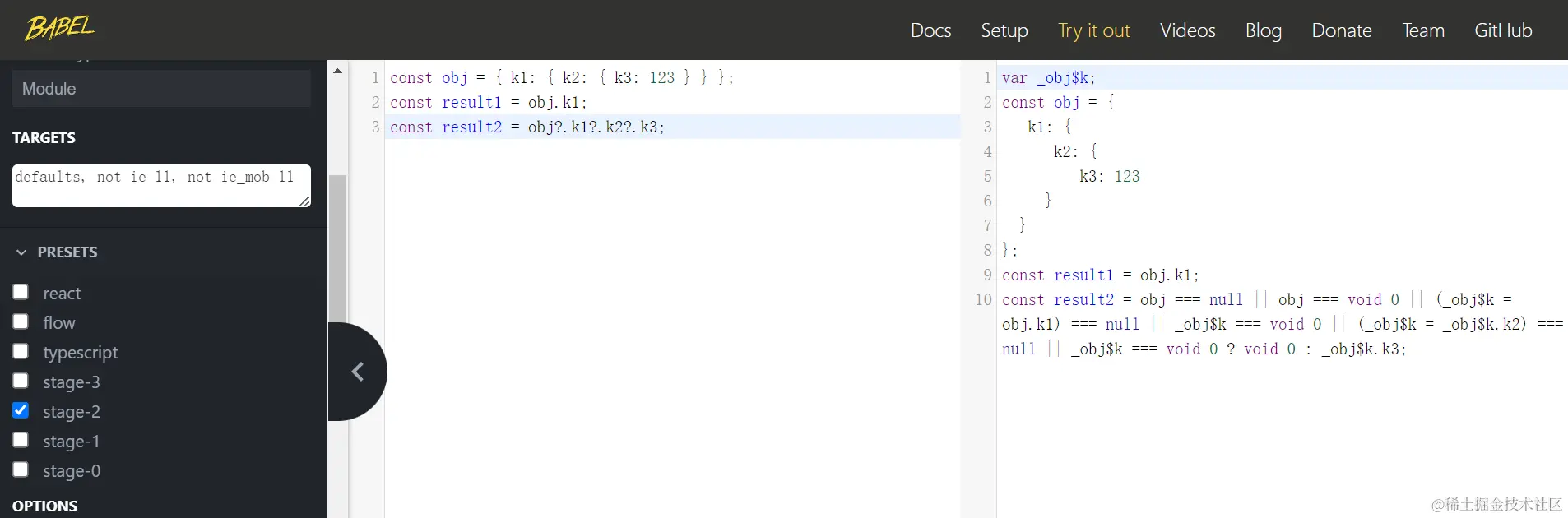
产量：厂商1的产量为q1，厂商2的产量为q2，市场总供给为Q=q1+q2。

市场出清价格P：市场总供给的函数P(Q)=8-Q (市场出清价格是可以将产品全部卖出的价格)

成本：设两个厂商都无固定成本，每增加一单位产量的边际成本c1=c2=c。

最后强调两个厂商同时决策,即决策之前都不知道另一方产量(完全信息静态博弈)。

该博弈两博弈方的策略空间是他们可以选择的产量。假设产量是连续变量，也就是说两厂商有无限多种可选策略。两博弈方的得益是两个厂商各自的利润，即各自的销售收益减去各自的成本：
$${\pi }_1=q_{1}P(Q)-q_{1}c=q_1(8-(q_1+q_2))-c{q}_1=-q_1^2-c{q}_1-q_1{q}_2+8q_1$$
和
$${\pi }_2=q_{2}P(Q)-q_{2}c=q_2(8-(q_1+q_2))-c{q}_2=-q_2^2-c{q}_2-q_1{q}_2+8q_2$$
其中，${\pi }_1$、${\pi }_2$分别是厂商1、厂商2的利润。可以看出，两博弈方的得益都取决于双方的产量。这个博弈中，我们需要找到纳什均衡，即只要策略组合$(q_1^{\ast },q_2^{\ast })$满足$q_1^{\ast }$和$q_2^{\ast }$相互是对于对方的最佳对策就构成纳什均衡。

根据纳什均衡的定义知道,纳什均衡就是相互是最优对策的各博弈方策略组合。因此,如果策略组合$(q_1^{\ast },q_2^{\ast })$是本博弈的纳什均衡,就必须是下列最大值问题的解：
$$\{\begin{array}{l}\underset{q_1}{\max }(-q_1^2-c{q}_1-q_1{q}_2^{\ast }+8q_1)\\ \underset{q_2}{\max }(-q_2^2-c{q}_2-q_1^{\ast }{q}_2+8q_2)\end{array}$$

2、模型求解

上述两个求最大值的式子都是各自变量的二次式,且二次项系数都小于0,因此只要$q_1^{\ast }$和$q_2^{\ast }$能使两式各自对$q_1$和$q_2$的导数为0就能实现两式的最大值。

即令
$$\{\begin{array}{l}-2q_1-c-q_2^{\ast }+8=0\\ -2q_2-c-q_1^{\ast }+8=0\end{array}$$

又因为策略组合$(q_1^{\ast },q_2^{\ast })$是本博弈的纳什均衡，故解下列方程
$$\{\begin{array}{l}-2q_1^{\ast }-c-q_2^{\ast }+8=0\\ -2q_2^{\ast }-c-q_1^{\ast }+8=0\end{array}$$

得到方程组唯一解:
$$\{\begin{array}{l}{q}_1^{\ast }=\frac{8-c}{3}\\ q_2^{\ast }=\frac{8-c}{3}\end{array}$$

可以进一步得到市场总供给
$$Q=q_1^{\ast }+q_2^{\ast }=\frac{16-2c}{3}$$
市场出清价格为
$$P=8-(16-2c)/3=\frac{8+2c}{3}$$
故双方的得益分别为:
$${\pi }_1=q_1^{\ast }P(Q)-q_1^{\ast }c=\frac{8-c}{3}\bullet (\frac{8+2c}{3}-c)=\frac{(8-c{)}^2}{9}$$
$${\pi }_2=q_2^{\ast }P(Q)-q_2^{\ast }c=\frac{8-c}{3}\bullet (\frac{8+2c}{3}-c)=\frac{(8-c{)}^2}{9}$$
总收益为(s为separate)：
$${\pi }_s^{\ast }={\pi }_1+{\pi }_2=\frac{2(8-c{)}^2}{9}$$
${\pi }_s^{\ast }$为两个厂商在各自做决策场景下的总收益。

3、模型拓展

如果从两个厂商总体利益最大化角度进行统一的产量选择,就要求实现两个厂商总和利润最大的总产量。设总产量为Q,则总利润为
$${\pi }_o=QP(Q)-cQ=Q(8-Q)-cQ=-Q^2+(8-c)Q$$
其中${\pi }_o$(o为overall)为两个厂商总体决策时的总利润，则同样求一阶导得到当$Q=(8-c)/2$时，取得最大值
$${\pi }_o^{\ast }=\frac{(8-c{)}^2}{4}$$

4、结果比较

将两个厂商进行统一的产量选择时的结果与两个厂商独立决策、追求各自利润最大化时的博弈结果相比:
$${\pi }^{\ast }=\{\begin{array}{l}\frac{2(8-c{)}^2}{9}，Q^{\ast }=\frac{(16-2c)}{3}\\ \frac{(8-c{)}^2}{4}，Q^{\ast }=\frac{(8-c)}{2}\end{array}$$

不难发现，从两个厂商总体利益最大化角度进行统一的产量选择时，总产量较小,而总利润却较高。

因此从两个厂商的总体来看,根据总体利益最大化决策效率更高，即如果两个厂商联合起来决定产量,先定出使总利益最大的总产量($\frac{8-c}{2}$)后各自生产其一半($\frac{8-c}{4}$),则各自可分享到单位利润$\frac{(8-c{)}^2}{8}$,比各自独立决策获得的利润$\frac{(8-c{)}^2}{9}$要高。

当然,在两个独立决策的企业之间实现合作并不容易。合作难以实现的原因主要是合作的产量组合($\frac{8-c}{4}$,$\frac{8-c}{4}$)不是纳什均衡。在这个策略组合中，双方都可以独自改变自己的策略得到更高的利润,双方都有突破$\frac{8-c}{4}$单位产量的冲动。在缺乏有强制性协议保障的情况下,这种冲动注定了不可能维持产量组合($\frac{8-c}{4}$,$\frac{8-c}{4}$)，两个厂商早晚都会增产，只有达到纳什均衡产量($\frac{8-c}{3}$,$\frac{8-c}{3}$)后才会稳定下来,因为这时任意一个厂商单独改变产量都不利于自己。如果将遵守还是突破限额作为厂商面临的选择,则构成如下图所示中得益矩阵表示的博弈。不难看出,下图所示是一个囚徒困境。

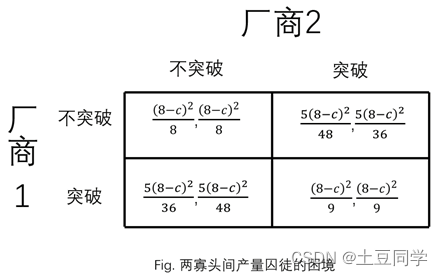
5、总结

上述博弈是根据谢识予老师的《经济博弈论》中连续产量古诺模型改编得到的比较简单版本。更复杂的模型可以包括n个寡头,市场出清价格与市场总产量的函数关系P=P(Q) 可以更复杂,每个厂商的成本也可以变化或不同。但不管这些因素如何变化,分析思路与上述模型是相似的,不过纳什均衡的产量组合将变成n个偏微分为0的联立方程组解。

产量博弈的古诺模型是一种囚徒困境,无法实现博弈方总体和各个博弈方各自最大利益的结论，该博弈说明自由竞争经济同样存在低效率问题，放任自流并非最好的政策。这些结论也说明了,政府对市场调控和监管的必要性。