归并排序的基本思想：

归并排序所采用的思想是将大问题分为小问题来处理，即我们常说的分治。

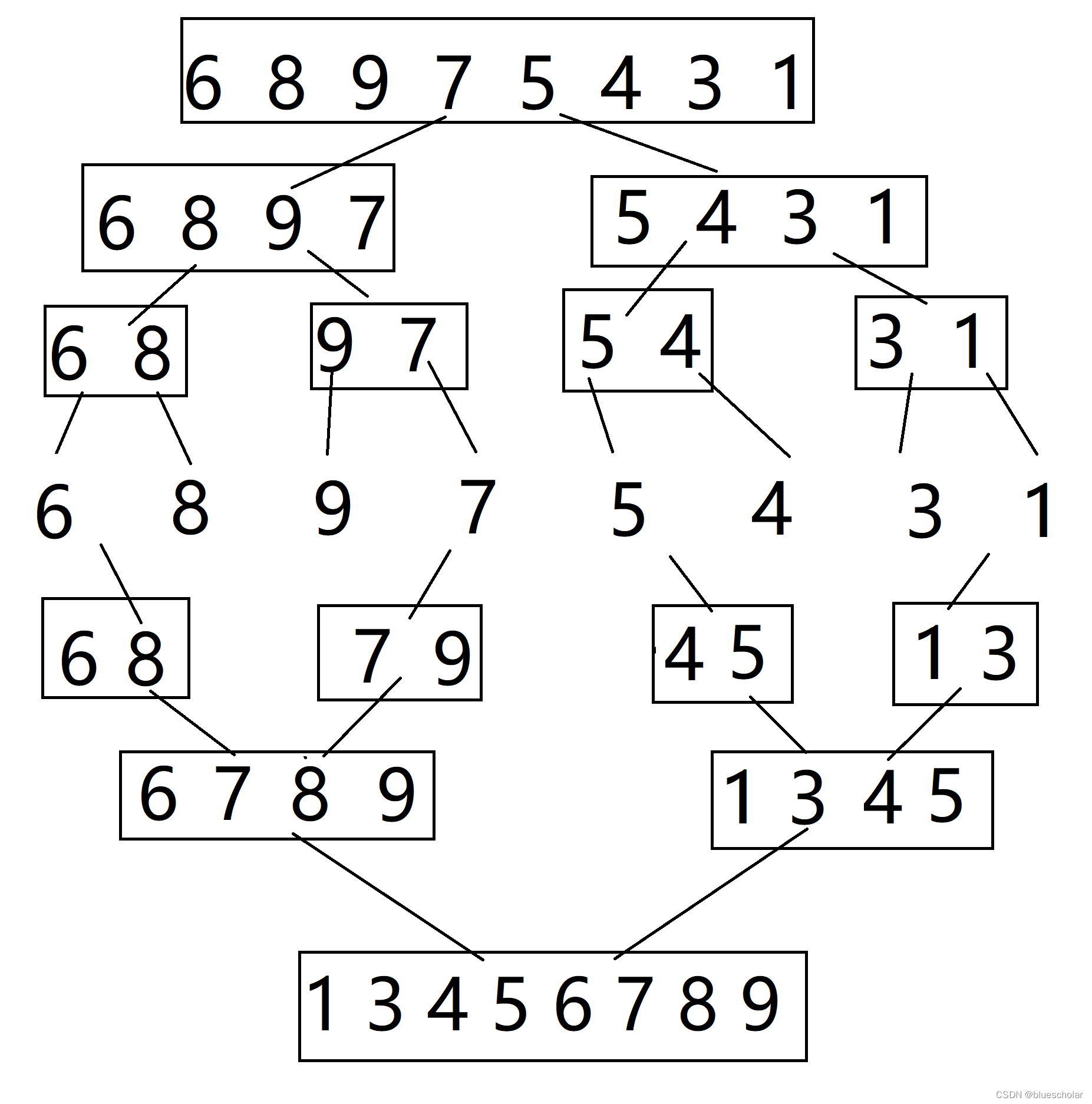
如图，要排序一个数组，我们就把这个数组往小的区间拆分，比如要排序数组，先排序左边数组，再排序右边数组，被分开的两个数组可以继续按照这种方式，继续分成更小的区间，直到每个区间只有一个数字的时候，再通过比较相邻区间来插入到数组中，当然，这里插入的数组我们需要额外开辟。

归并排序的逻辑我们理清楚后，有两种方式来实现：递归和非递归，我们分别来介绍一下

递归算法：

递归算法的思路分析：

显然归并排序将大问题分治为小问题的思想是非常显然也是很适合用递归去解决的

写好递归逻辑的代码，由于我们需要开辟数组,因此我们将递归代码单独封装成另一个函数，在开辟数组的函数里调用就可以：

开辟数组的函数：

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	_MergeSort(a,0,n-1,tmp);

	free(tmp);
	tmp = NULL;
}

递归的函数：

void _MergeSort(int* a,int begin,int end,int* tmp)
{
	if (begin >= end)
	{
        //如果开始大于等于结束，意味着只有一个数据，可以直接返回
		return;
	}
	
	int mid = (begin + end) / 2;
	//递归使子区间有序
	_MergeSort(a,begin, mid, tmp);
	_MergeSort(a,mid+1, end, tmp);

	//归并[begin,mid] [mid+1,end]
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
    //每个区间的i都是不同的，因此i要从begin开始
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
    //如果某个区间还剩下数据，直接插入到tmp的后面
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	memcpy(a+begin,tmp + begin,sizeof(int)*(end - begin + 1));
}

非递归算法：

非递归的思路分析：

归并排序的递归算法非常简单且容易理解，我们主要来看非递归算法：

非递归算法本质也是分治的思想，只不过在非递归算法这里，我们直接从一个一个的数据开始排序

第一次排序范围：0~0 1~1 2~2 3~3 4~4 5~5 6~6 7~7（每组一个）

第二次排序范围：0~1 2~3 3~4 4~5 5~6 6~7（每组两个）

第三次排序范围：0~3 4~7（每组四个）

int rangeN = 1;
	while (rangeN < n)
	{
		for (int i = 0;i<n;i+=2*rangeN)
		{
			int begin1 = i, end1 = i + rangeN - 1; 
			int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;

			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}


			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
		memcpy(a,tmp,sizeof(int)*n);
		rangeN *= 2;
	}

边界问题：

弄清楚非递归是如何处理数据的，我们还需要考虑一个问题：边界问题

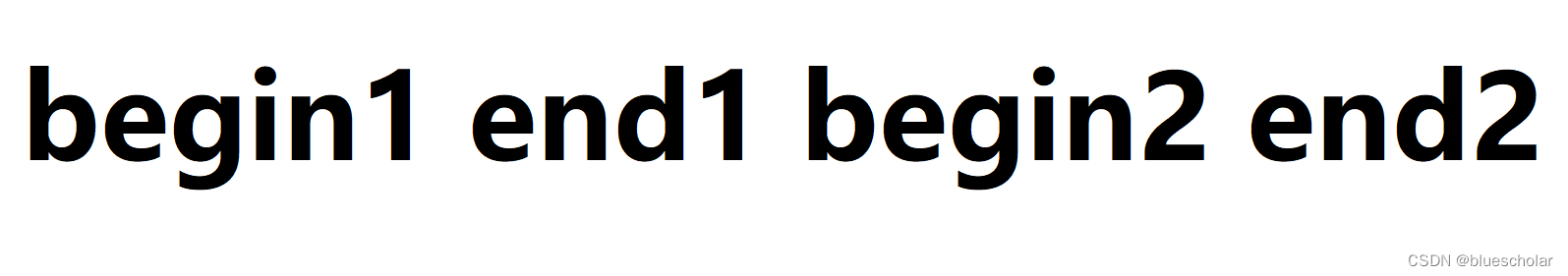
上述四个变量中，有三种越界的情况：end1越界，begin2越界，end2越界

针对上述问题，我们要修改对应的边界，防止越界：

void MergeSortNONR(int* a,int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		exit(-1);
	}
	int rangeN = 1;
	while (rangeN < n)
	{
		for (int i = 0;i<n;i+=2*rangeN)
		{
			int begin1 = i, end1 = i + rangeN - 1; 
			int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;

			int j = i;
			if (end1 >= n)
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}


			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
		memcpy(a,tmp,sizeof(int)*n);

		rangeN *= 2;
	}
}