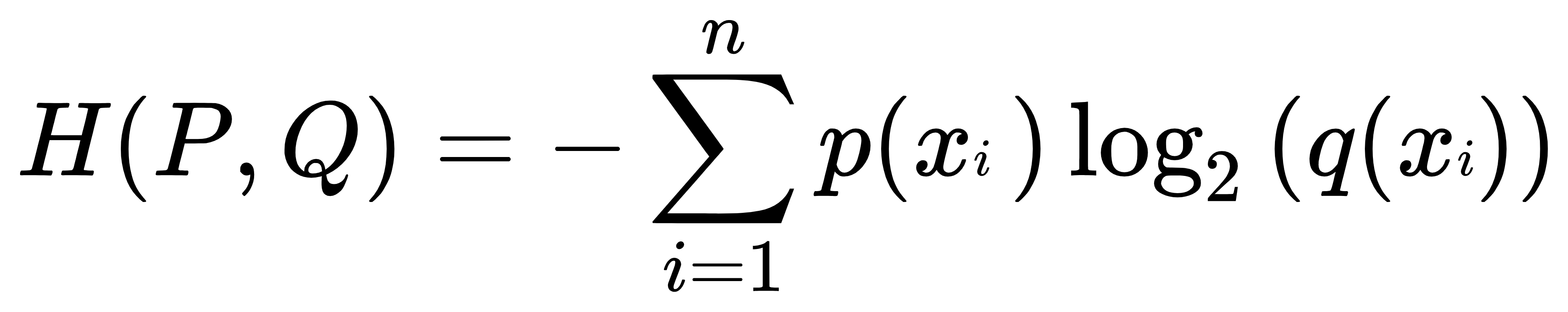1、前言
- 我们在训练神经网络时，最常用到的方法就是梯度下降法。在了解梯度下降法前，我们需要了解什么是损失(代价)函数。所谓求的梯度，就是损失函数的梯度。
- 如果不知道什么是梯度下降的，可以看一下这篇文章：机器学习入门教学——梯度下降、梯度上升_恣睢s的博客-CSDN博客
- 损失函数其实就是神经网络里的标准和期望的标准相差多少的定量表达。（现有模型与期望模型的质量差距）
- 损失函数越小，现有模型就越逼近期望模型，现有模型的精度也就越高。
- 【注】损失函数和代价函数可以看作是两个概念不同的名字，但代表的函数和作用完全一样，通常可以互相替换使用，没有实质区别。
- 损失函数该如何设计呢？这里有三种方法：最小二乘法、极大似然估计法、交叉熵法。
- 机器学习入门教学——损失函数（最小二乘法）
- 机器学习入门教学——损失函数（极大似然估计法）
- 机器学习入门教学——损失函数（交叉熵法）
2、交叉熵法
- 交叉熵法是先把模型换成熵(数值)，然后再用熵去比较不同模型之间的差异。
- 在了解交叉熵之前，我们先了解以下几个概念。
2.1、信息量
2.1.1、定义
- 信息的作用是消除事件的不确定性，信息量就是信息能消除事件不确定性的程度。
- 例如：
- 掷骰子猜点数时，告诉你一个消息再猜点数。下面三条消息消除不确定性的程度是逐渐增大的，其消息量也是逐渐增大的。
- 我们分别来看上面三条消息发生的概率：
- 骰子的点数大于0：P=1
- 骰子的点数大于3：P=1/2
- 骰子的点数是5：P=1/6
- 我们会发现这些消息发生的概率是逐渐减小的。
- 所以，信息量的大小与信息发生的概率成反比。概率越大，信息量越小；概率越小，信息量越大。
- 设信息描述的事件为x，其发生的概率为P(x)，则信息量的公式为：
-
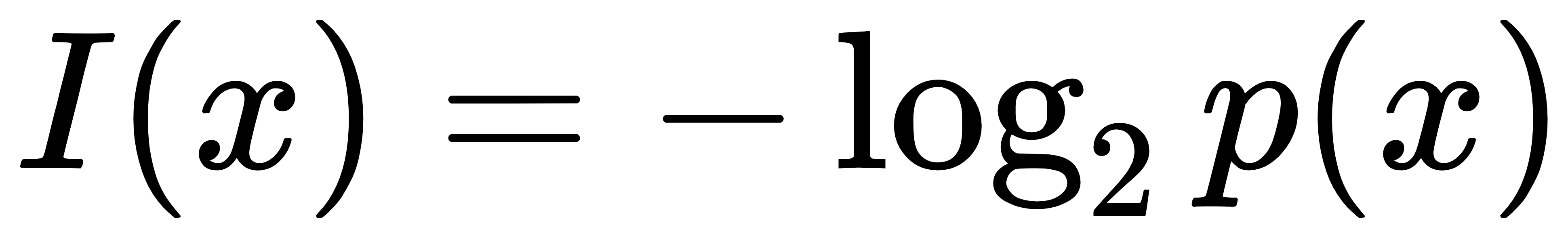（具体怎么来的就不阐述了），单位为：比特bit
-
2.1.2、计算
- 假设，我们现在要给计算机输入一个十六位的数据。在输入数据之前，这16位数据都可以取0或1，这个数据的概率就是
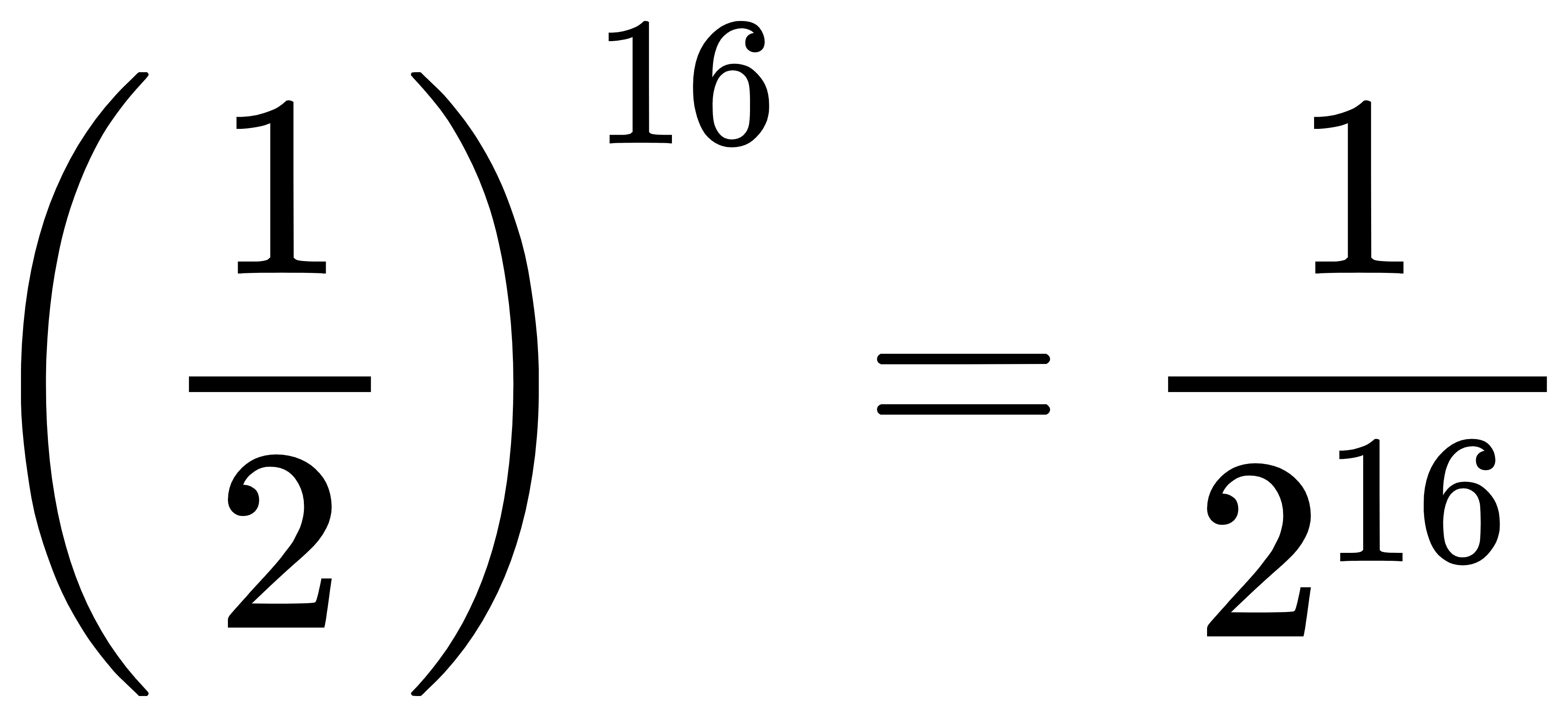。当输入这个数据后，这个数据是已知的了，它的概率就变成了1。那这个数据的信息量是多少呢？
- 这个数据的信息量为16比特。
2.2、信息熵
2.2.1、定义
- 信息量是衡量某个具体的事件，而信息熵是衡量整个系统中的所有事件，即一个系统从原来的不确定到确定难度有多大。
- 信息熵也称为熵，可以表示为所有信息量的期望。所以，信息熵的公式为：
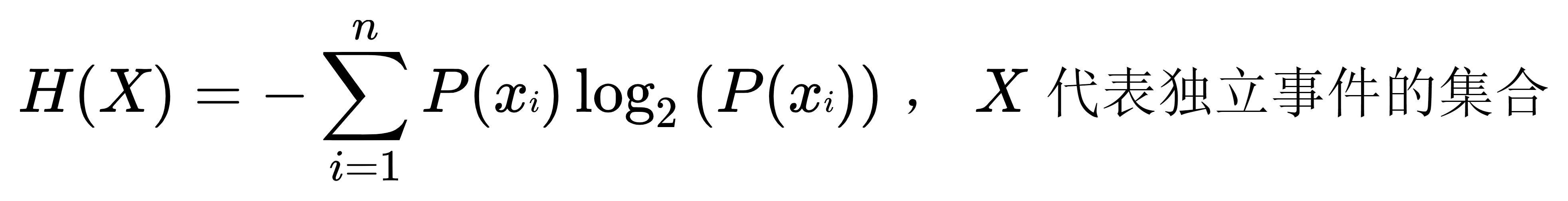，单位为：比特
- 熵代表了随机变量的不确定性（即混乱程度）。熵越大，代表随机变量的不确定性越大。当变量可取值的种类一定时，其取每种值的概率分布越平均，其熵值越大。
2.2.2、计算
- 假设我们要预测一场球赛的输赢，求它的信息熵。已知法国队赢球的概率是99%，中国队赢球的概率是1%。
- 法国队赢球的信息量为：
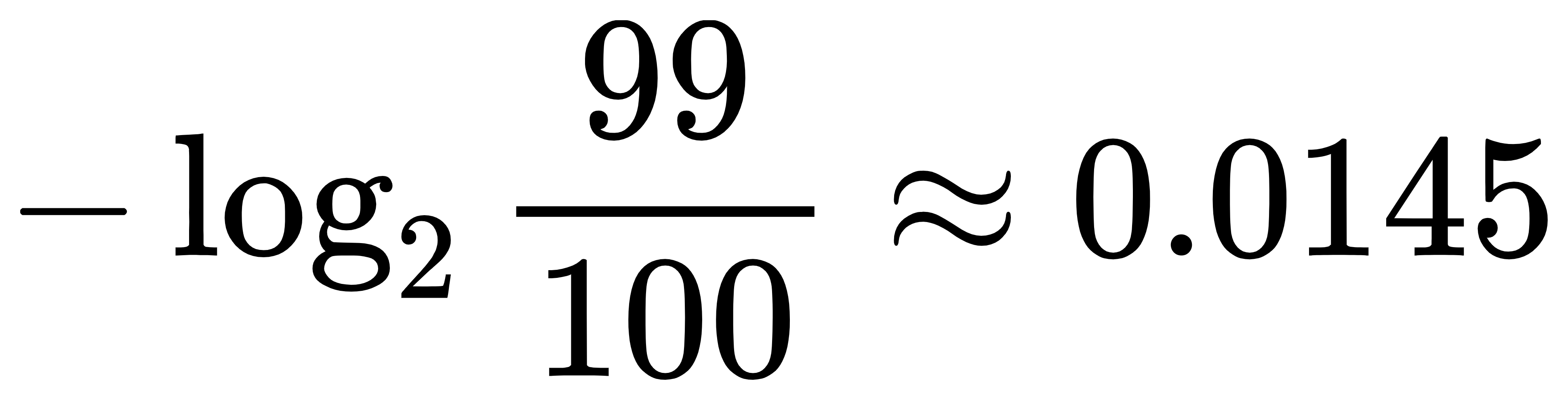
- 中国对赢球的信息量为：
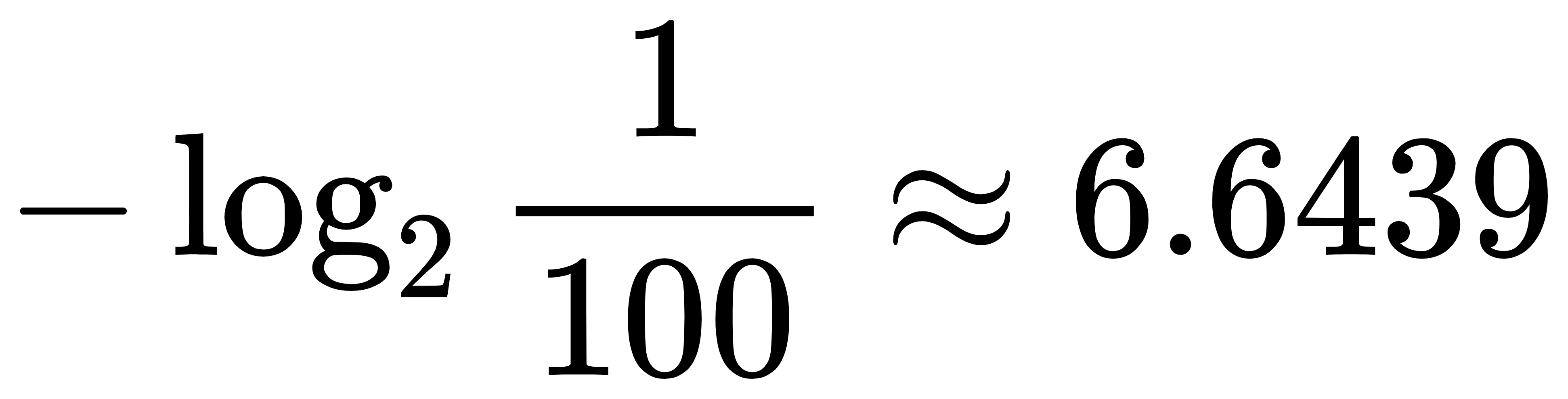
- 信息熵为：
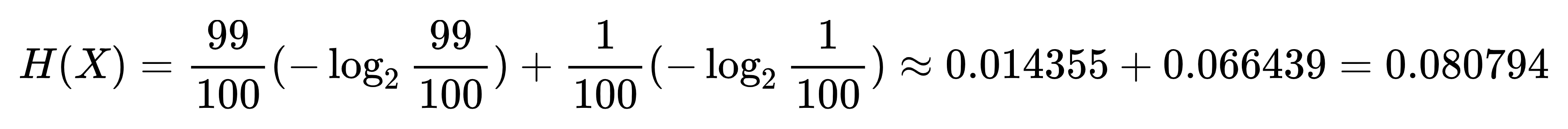
2.3、相对熵（KL散度）
- 比较两个模型，就可以把两个模型的的熵计算出来，再直接比较它们的熵。但是期望模型是未知的，无法直接求熵。那就不得不提到相对熵了。
- 如果对于同一个随机变量X，有两个单独的概率分布P(X)和Q(X)，则我们可以使用KL散度来衡量这两个概率分布之间的差异。
- 例如：下面有两个模型的概率分布。
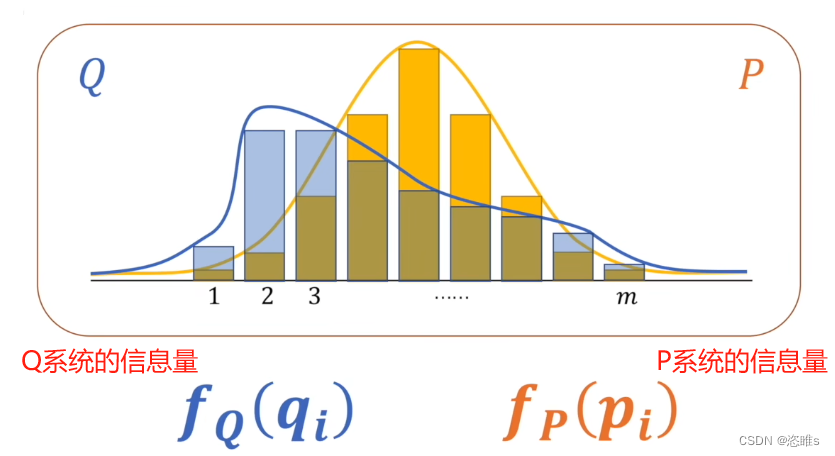
- 以下就是它们相对熵的计算公式：
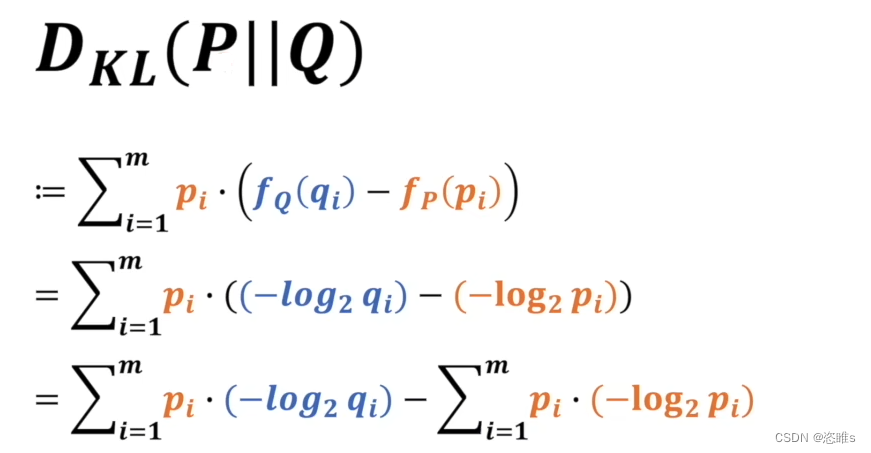，其中
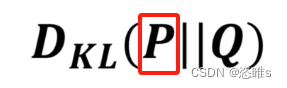P在前，表示以P系统为基准去考虑P和Q相差多少。- 【注】以P或以Q为基准性质是不同的。
- 其实就是P、Q系统中对应事件的信息量的差值，再求整体期望。
- 如果Q和P相等，那相对熵就为0。简单来说，就是Q要达到和P一样的分布的话，还差了多少信息量。
- 观察发现，
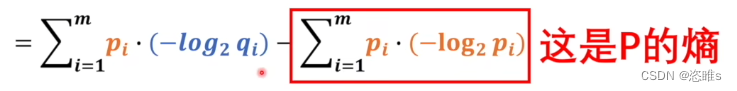，P作为基准时熵是不变的，只需要考虑前面一部分。 - 而前面一部分就是交叉熵了，
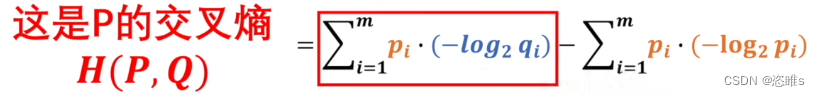
2.4、交叉熵
- 我们已经知道，KL散度 = 交叉熵 - 信息熵
- 交叉熵的公式表示为：
- 由结论可知，KL散度一定是大于等于0的。所以交叉熵是一定大于等于信息量，并且大于0的。（不用深究原因）
- 这时如果要让Q的概率模型和P的概率模型非常接近的话，就要找到交叉熵的最小值。也就是说交叉熵本身就可以作为损失函数。
2.5、运用
- 既然已经知道了交叉熵可以作为损失函数，那么交叉熵中的一些变量在神经网络中应该用什么进行替换呢？
- 我们还是用之前判断图片是不是猫的例子。
- 首先，
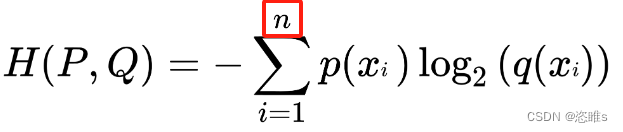中的n代表输入图片的数量。 - 因为P为基准，也就是被比较的模型，所以P是理想模型。而Q是比较的模型，也就是现有模型。那么其中的
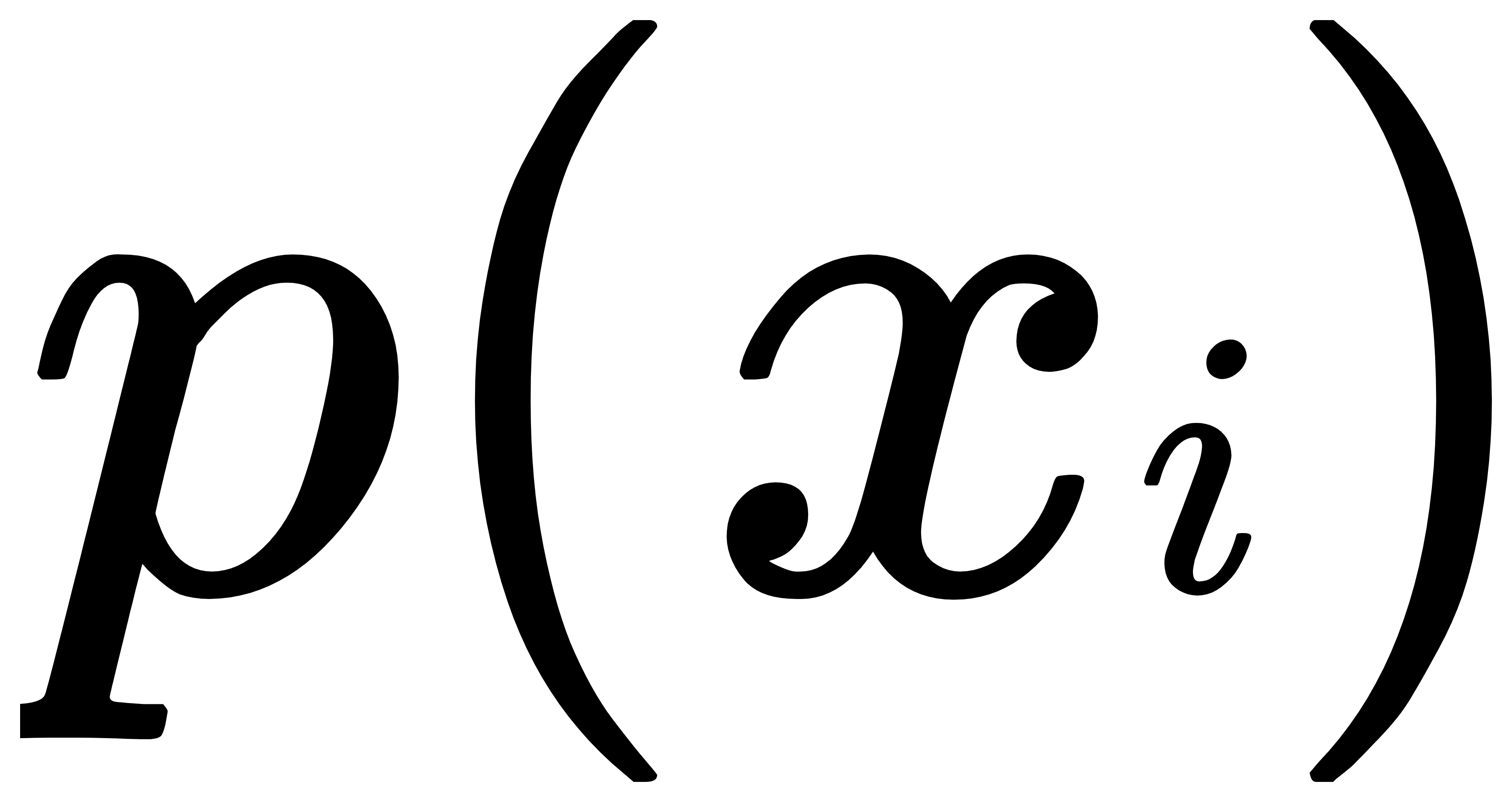就应该是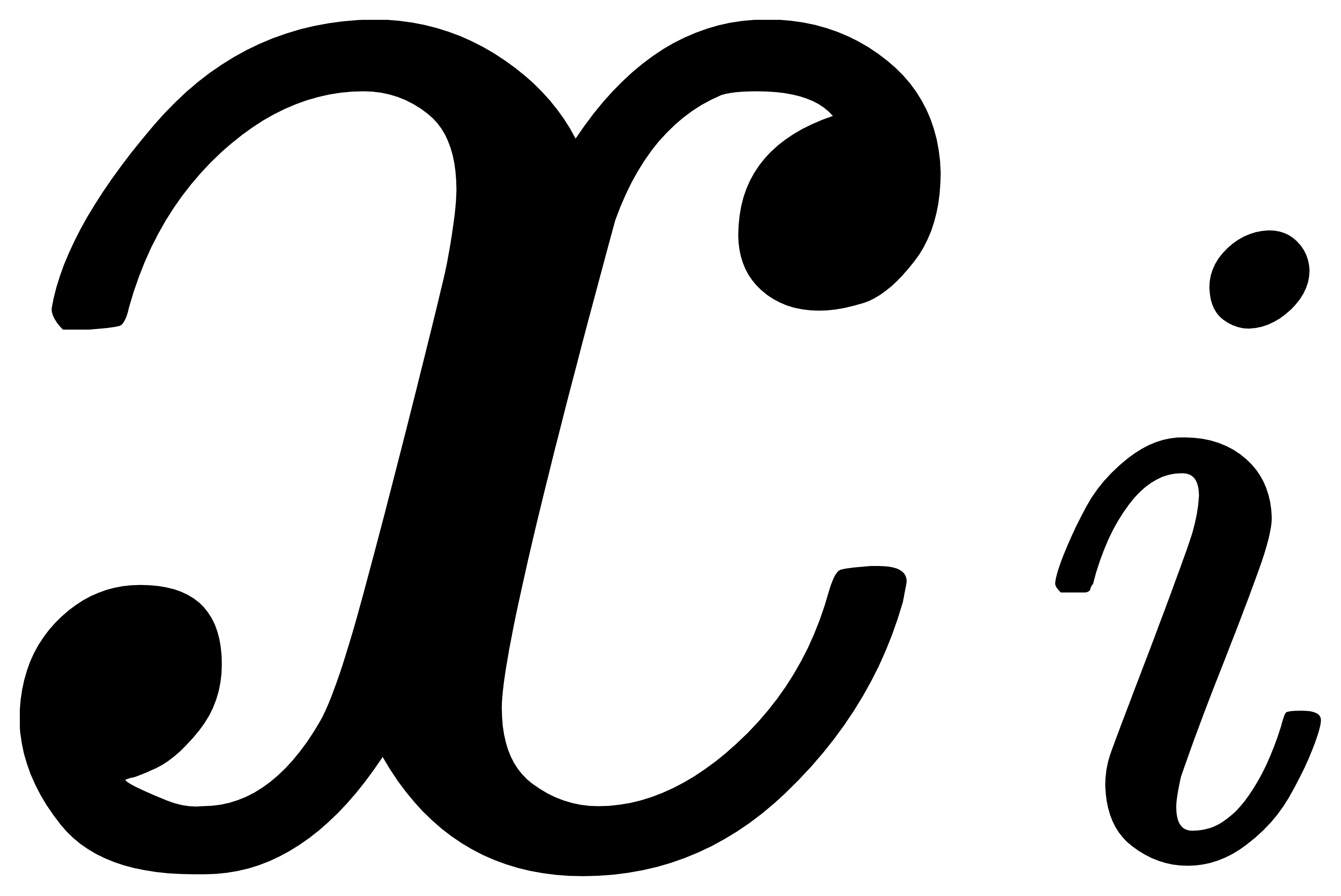
是猫和不是猫的概率，
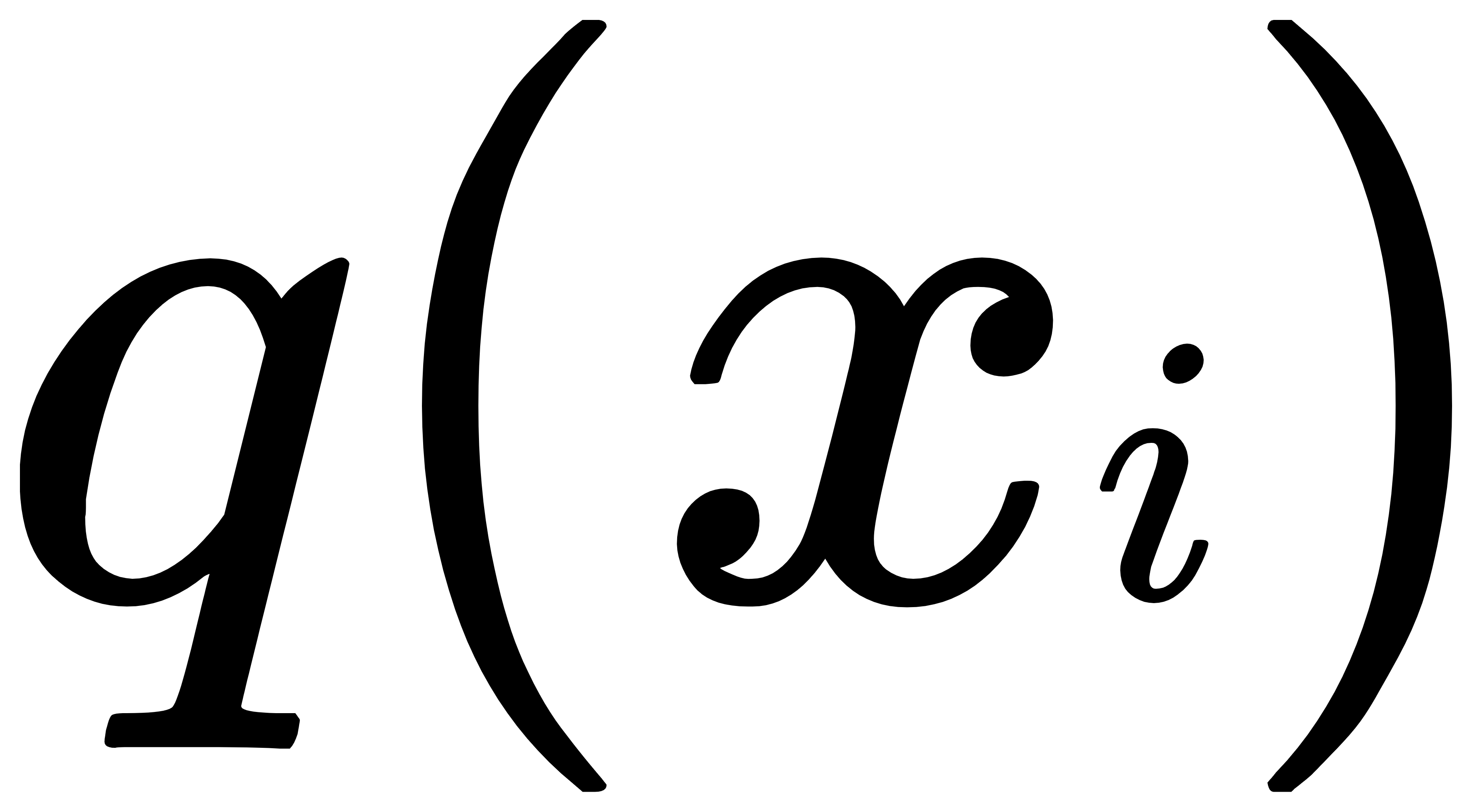就应该是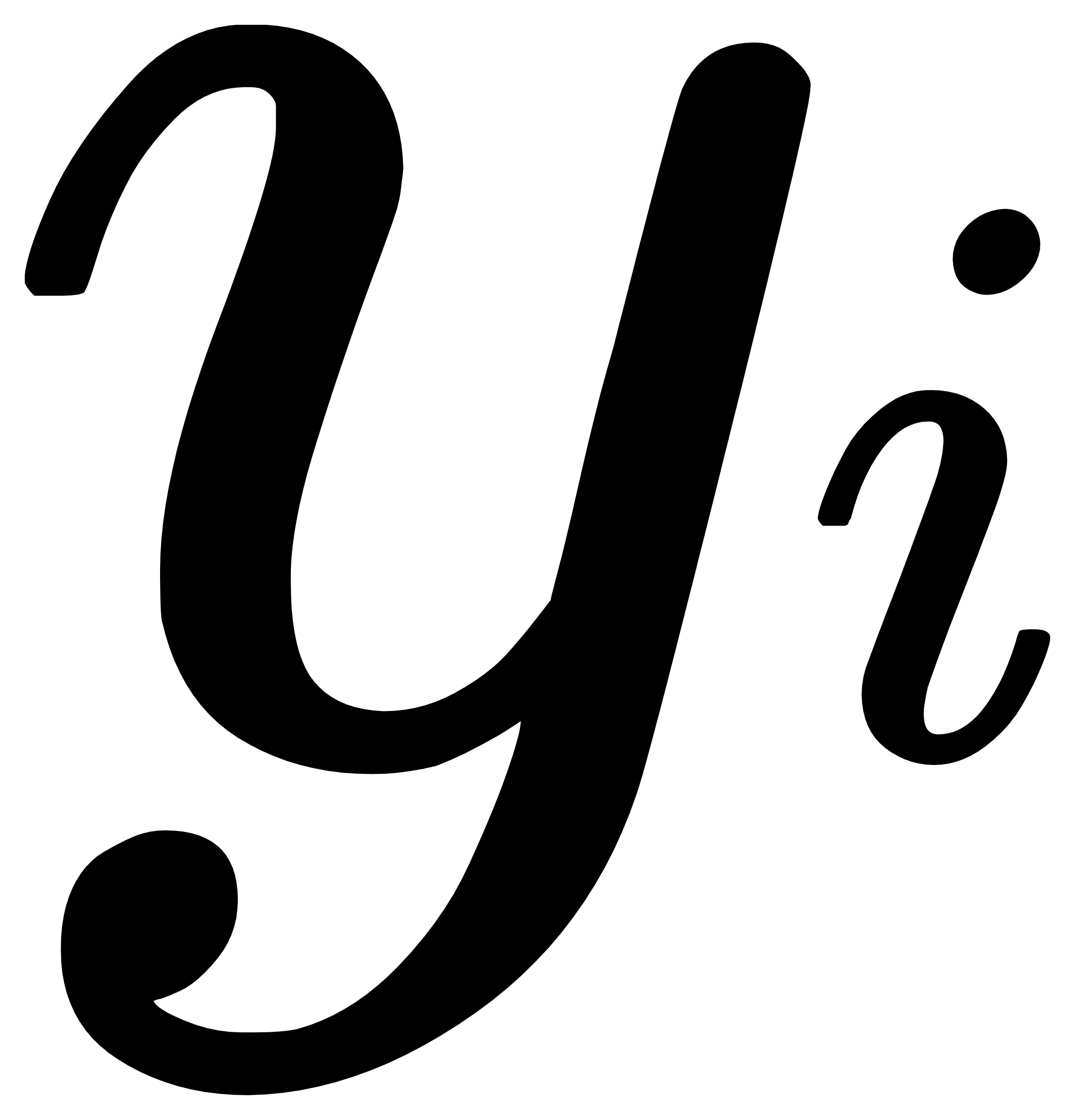
是猫和不是猫的概率。 - 转换之后就是：
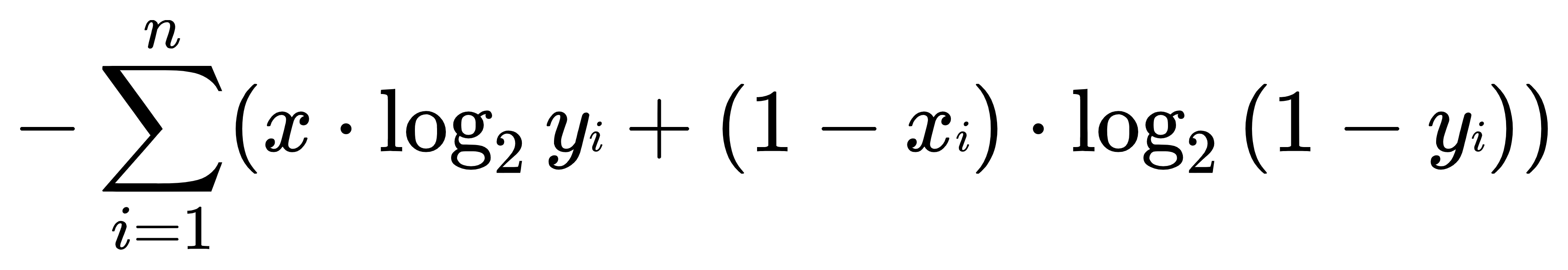
- 这个公式和极大似然估计作为损失函数的公式是一样的。
3、交叉熵法和极大似然估计法的区别
- 虽然两者在形式上是相同的，但是在物理层面还是有很大区别的。
- 极大似然估计中引入log是为了把连乘换做连加，底数为几是无所谓的；而交叉熵中log以2为底是定义中给出的，是固定的，它代表最后计算出来的单位是比特。
- 极大似然估计法本来是求最大值，只是为了适应损失函数才加了个负号改成求最小值；而交叉熵的负号是定义中给出的。
