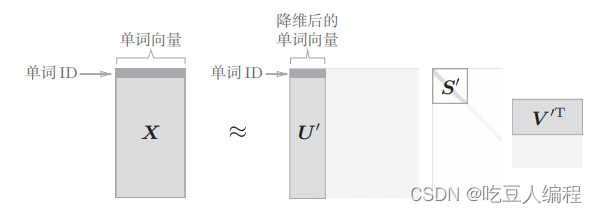
题目描述：

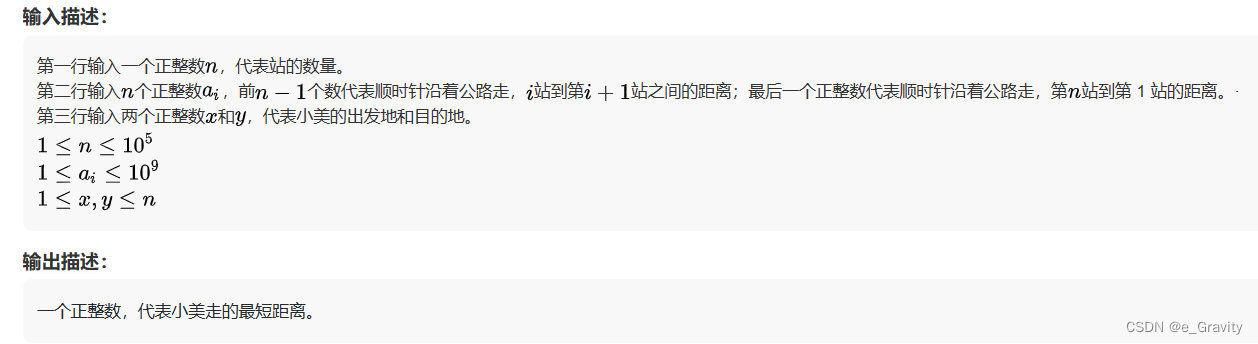
有一个环形的公路，上面共有n站，现在给定了顺时针第i站到第i+1站之间的距离（特殊的，也给出了第n站到第 1 站的距离）。小美想沿着公路第x站走到第y站，她想知道最短的距离是多少？

看到这题还以为是考察双链表 o.O    

一般遇到带环的问题，有个技巧：破环成链. 之前刷题有道石子合并的升级版（环形石子【区间dp】)也是这个套路。

当破成链之后  问题就变成 已知每俩个节点相邻的距离，求中间某段的距离

这就转化成了前缀和的问题, s[i]定义成i节点到节点1的距离，则x到y的距离就是s[y]-s[x] 

有个细节，因为不知道x在前，还是y在前，所以取绝对值，也就是abs(s[y]-s[x]); 还有另外一条方向也有可能是最短的，拿总距离减去之前算的就是这方向的距离，俩个取min就是答案。

注意long long的问题，因为俩个点之前的距离最大是1e9，总距离可能爆int。

#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N];
LL s[N];
int n;
int main()
{
	cin >> n;
	LL ans = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		s[i + 1] = s[i] + a[i];
	}
	int x, y;
	cin >> x >> y;
	LL ans1 = abs(s[y] - s[x]);
	LL ans2 = s[n + 1] - ans1;
	cout << abs(min(ans1, ans2)) << endl;
	return 0;
}

Linux 启动！