文章目录
- 1. 偏微分方程和常微分方程
- 1.1 偏微分
- 1.2 常微分
- 2. 表示方法(名词/notation)
- 2.1 莱布尼兹表示
- 3. 空间直线及其方程
- 4. 方向向量
- 4.1 两点求方向向量
高数课本(有目录)可以看这个链接:1. 高等数学第六版.同济大学数学系.扫描版.pdf
1. 偏微分方程和常微分方程
1.1 偏微分
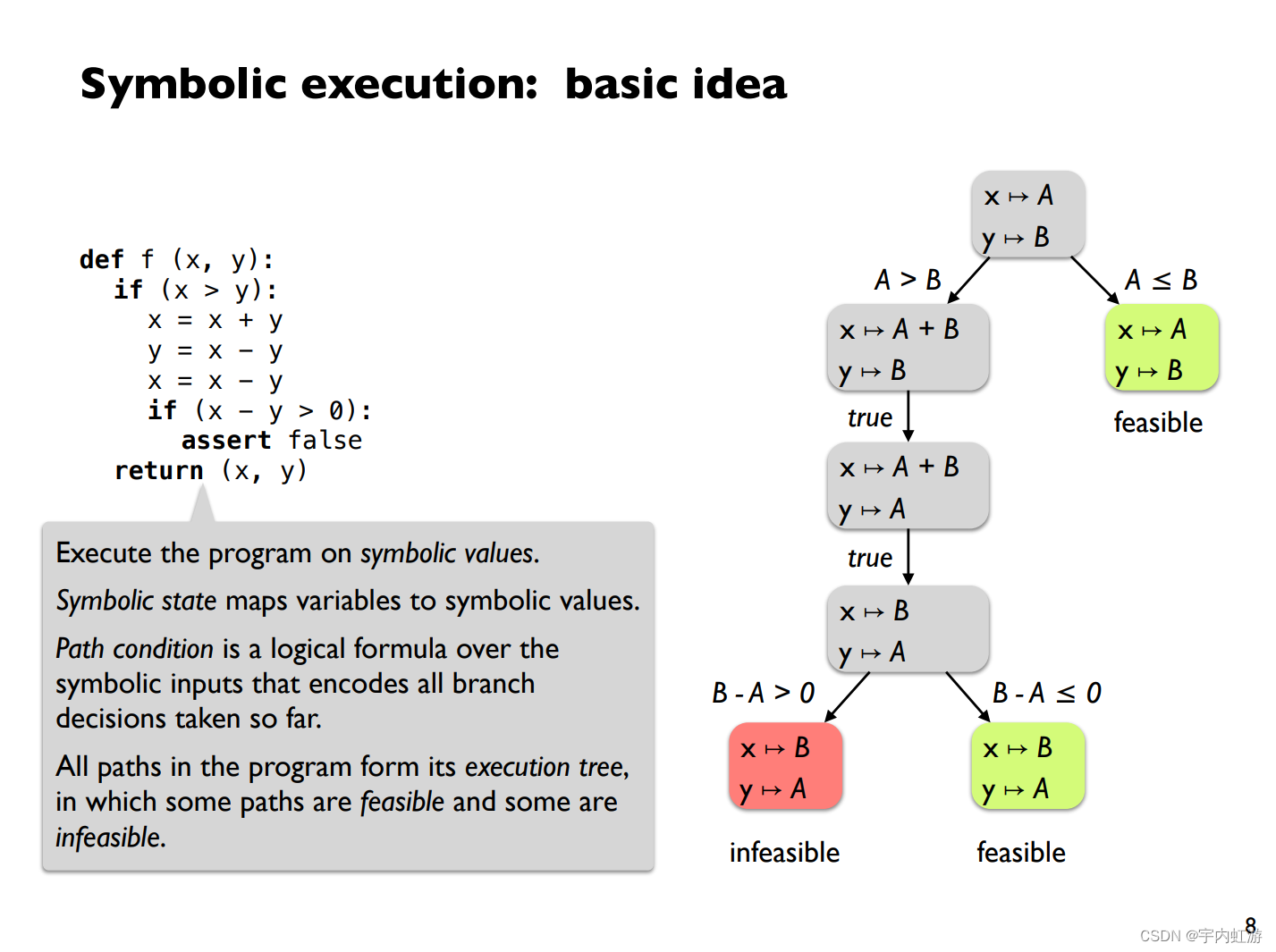
水平集中,见到了偏微分方程

- 包含未知函数的偏导数(或偏微分)的方程。
- 方程中所出现未知函数偏导数的最高阶数,称为该方程的阶。
参考:
- 百度百科:偏微分方程
1.2 常微分
2. 表示方法(名词/notation)
2.1 莱布尼兹表示

参考:
- 莱布尼茨公式
3. 空间直线及其方程
感谢百度文库的PPT:空间直线的点向式方程和参数方程。让我想起来自己好像学过这个东西,在高数里。
高数书下册->第八章 空间解析几何与向量代数->第六节 空间直线及其方程
- 完整的可以直接看博客:空间直线的几种方程,这个人贴的比较全
- 我这里只贴自己用到的部分

4. 方向向量
4.1 两点求方向向量
感谢:已知两点坐标如何求两点连线的方向向量
已知两点A( x 1 x_1 x1, y 1 y_1 y1),B( x 2 x_2 x2, y 2 y_2 y2),则向量AB=( x 2 − x 1 x_2-x_1 x2−x1, y 2 − y 1 y_2-y_1 y2−y1)
即向量AB为B点坐标减A点坐标。
例如:
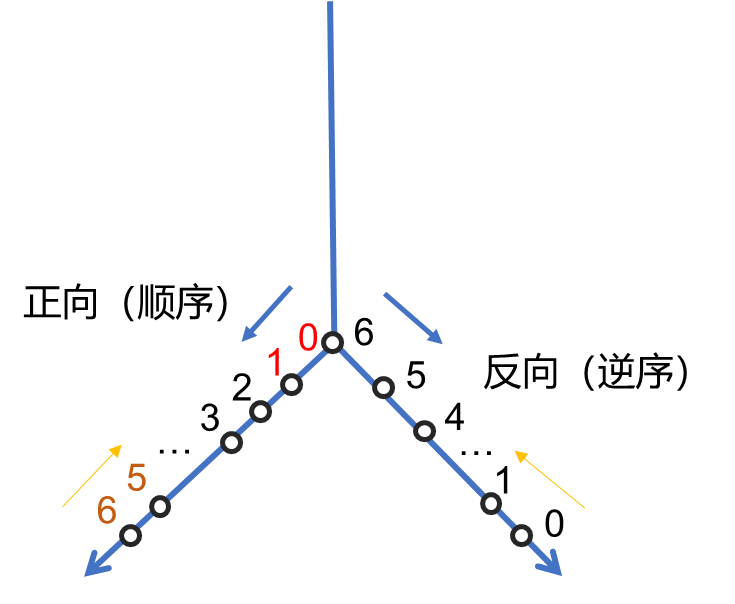
对于上面这样的序号0-6的点,以左侧为例。
要计算 01 → \overrightarrow{01} 01的方向向量,也就是用序号 1 1 1的坐标减去序号 0 0 0的坐标