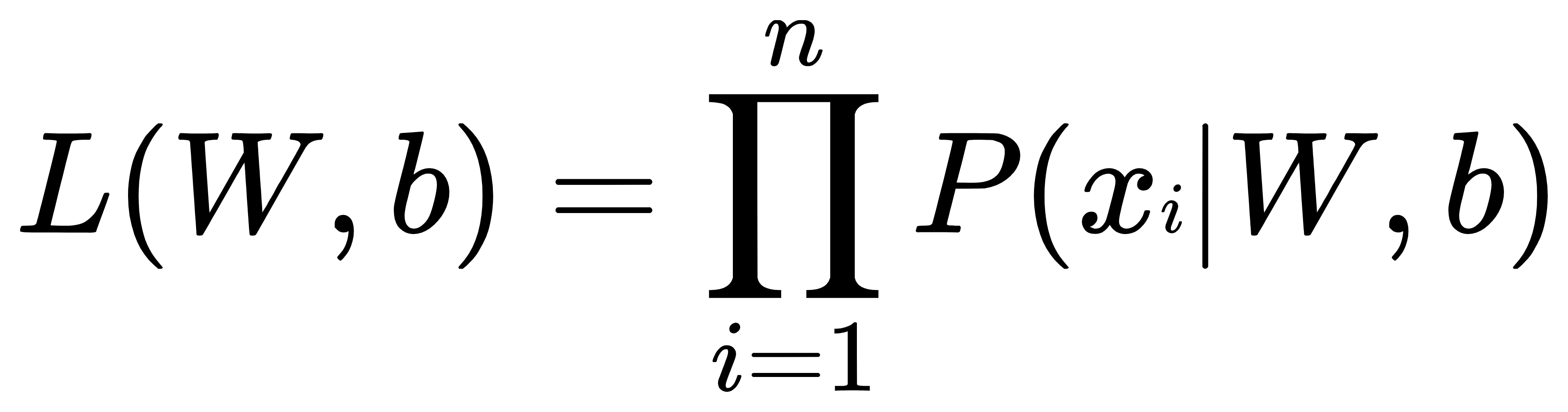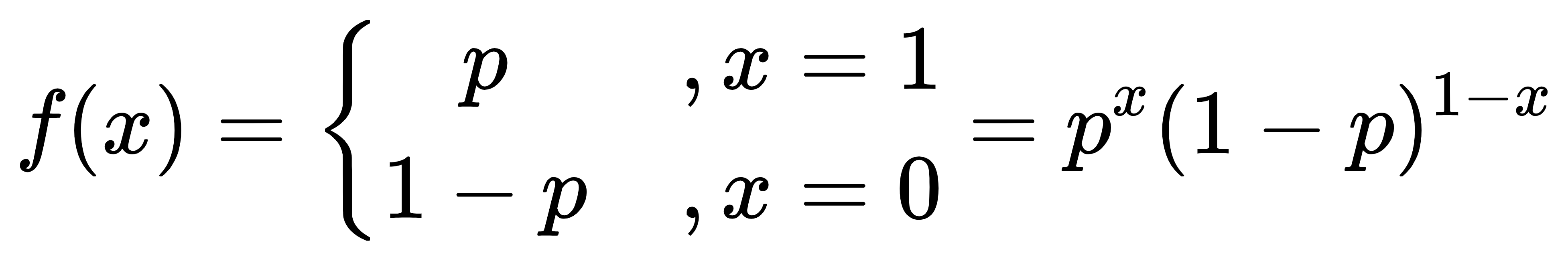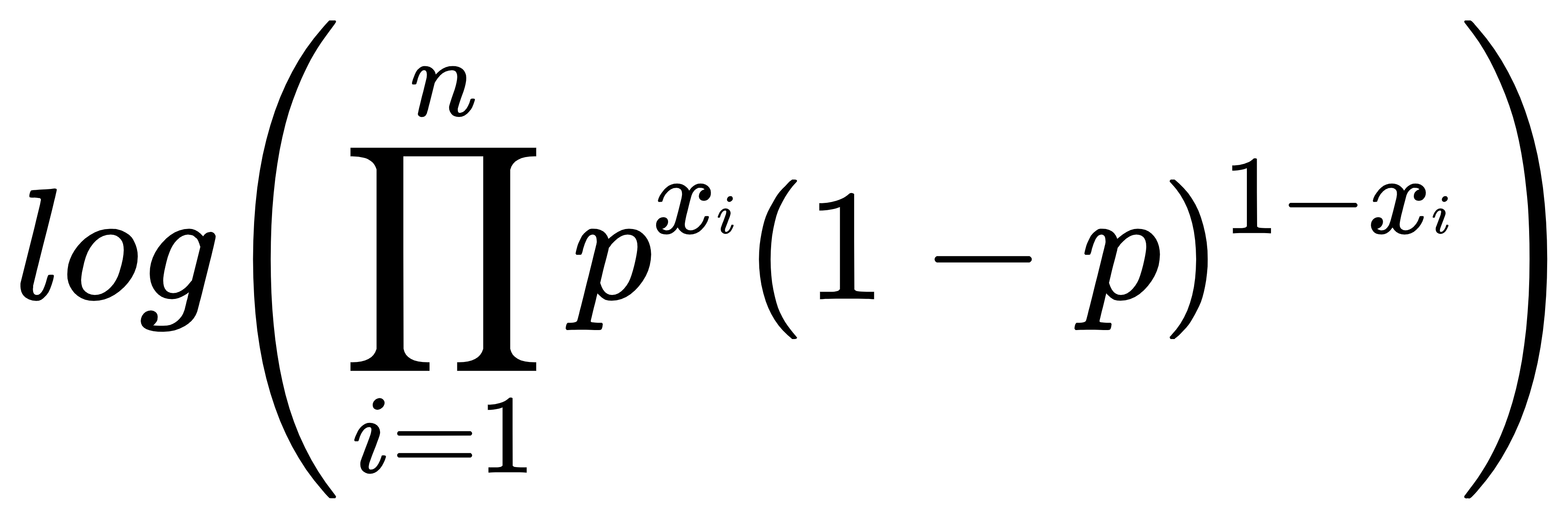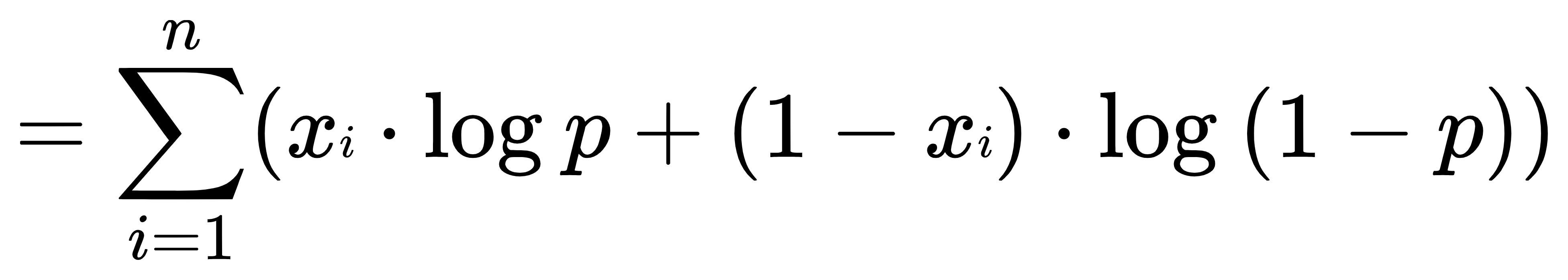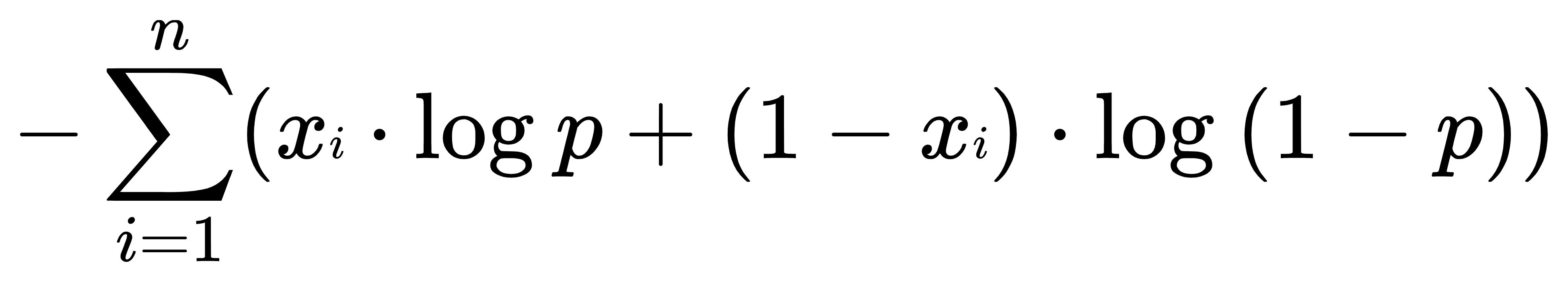1、前言
- 我们在训练神经网络时,最常用到的方法就是梯度下降法。在了解梯度下降法前,我们需要了解什么是损失(代价)函数。所谓求的梯度,就是损失函数的梯度。
- 如果不知道什么是梯度下降的,可以看一下这篇文章:机器学习入门教学——梯度下降、梯度上升_恣睢s的博客-CSDN博客
- 损失函数其实就是神经网络里的标准和期望的标准相差多少的定量表达。(现有模型与期望模型的质量差距)
- 损失函数越小,现有模型就越逼近期望模型,现有模型的精度也就越高。
- 【注】损失函数和代价函数可以看作是两个概念不同的名字,但代表的函数和作用完全一样,通常可以互相替换使用,没有实质区别。
- 损失函数该如何设计呢?这里有三种方法:最小二乘法、极大似然估计法、交叉熵法。
- 机器学习入门教学——损失函数(最小二乘法)
- 机器学习入门教学——损失函数(极大似然估计法)
2、极大似然估计法
2.1、似然
- 在了解极大似然估计时,我们先要弄清楚什么是似然。
- 似然和概率都是统计学中非常重要的概念,了解似然之前,我们先了解什么是概率。
- 概率是指某个特定环境下某件事情发生的可能性。
- 例如,在抛硬币前,根据硬币的性质,我们可以推测任何一面朝上的可能性是50%。
- 例如,在抛硬币前,根据硬币的性质,我们可以推测任何一面朝上的可能性是50%。
- 似然和概率恰好相反。它是基于已经确定的结果,来推测产生这个结果的可能环境。
- 例如,我们随机抛1w次硬币,得到8000次人像,2000次数字。从而推断出人像朝上的概率是0.8,数字朝上的概率是0.2。
- 例如,我们随机抛1w次硬币,得到8000次人像,2000次数字。从而推断出人像朝上的概率是0.8,数字朝上的概率是0.2。
- 假设,θ是环境对应的参数(上述案例中,θ为0.8),x是事件发生的结果。
- 概率:
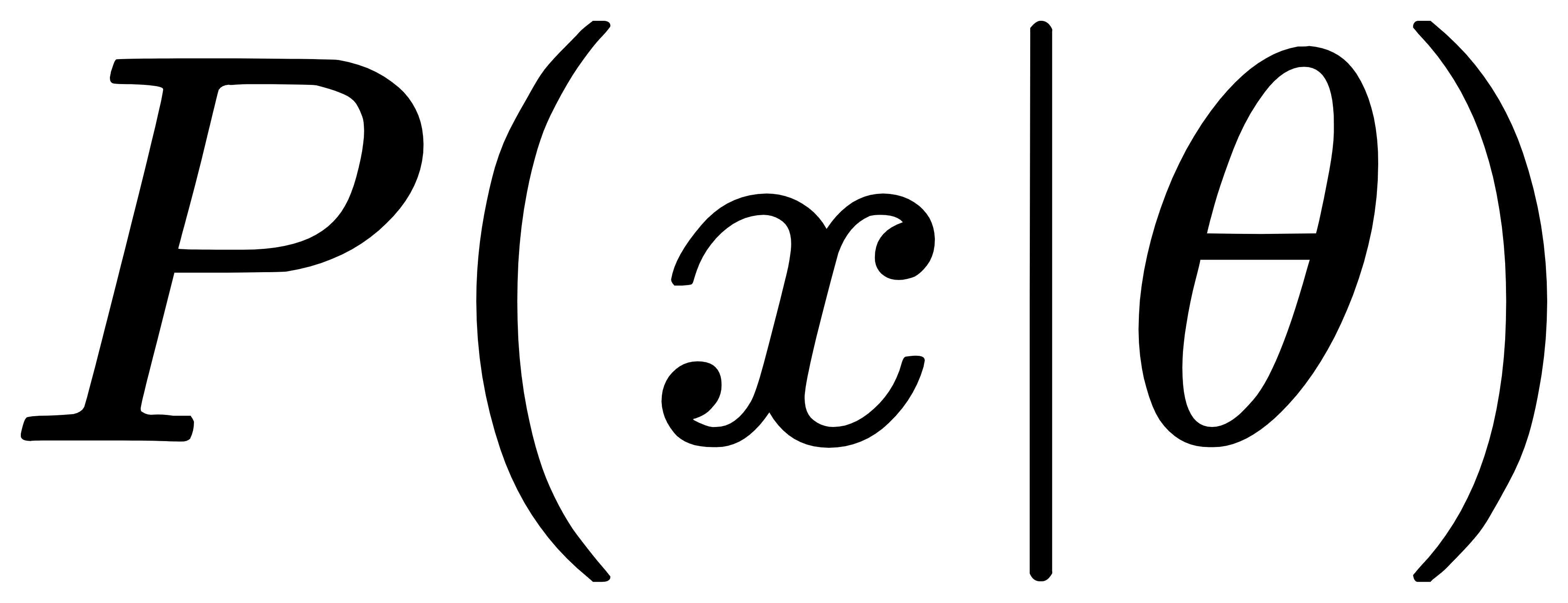 ,即在环境参数θ的条件下,x发生的概率。P是关于x的函数。
,即在环境参数θ的条件下,x发生的概率。P是关于x的函数。 - 似然:
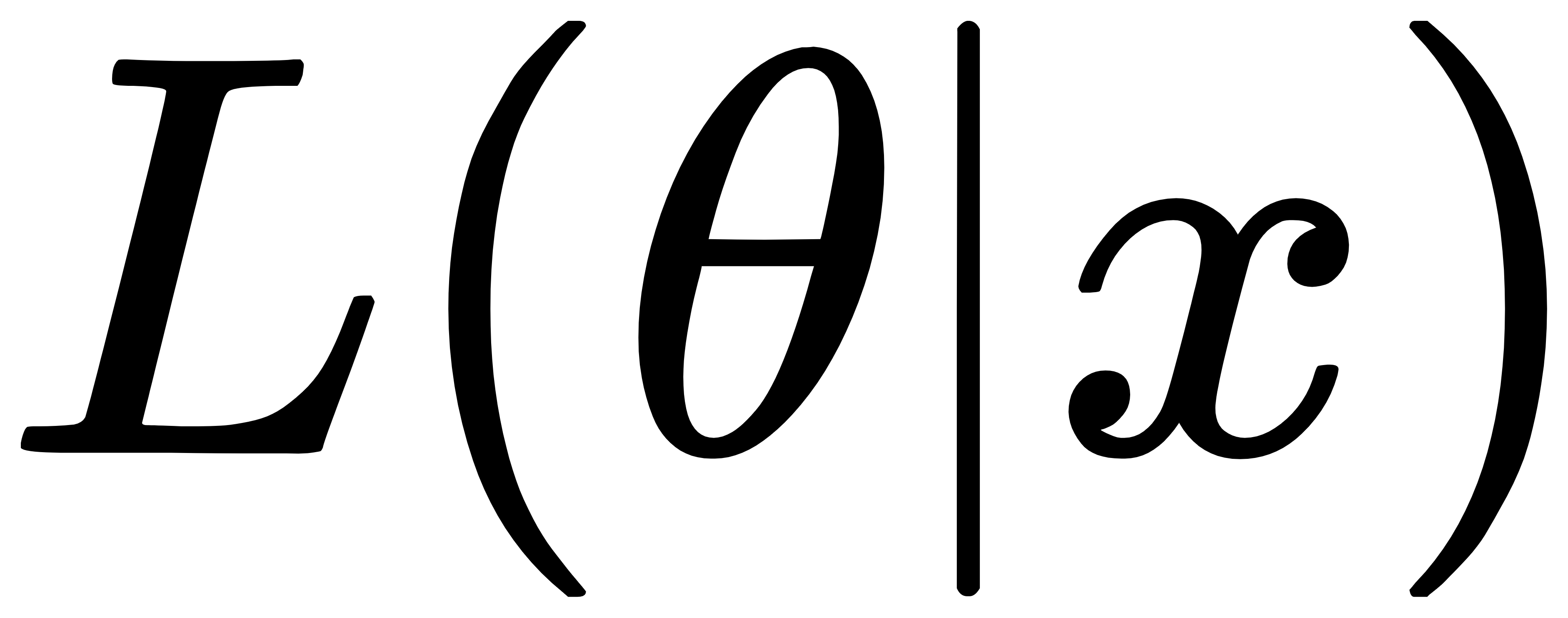 ,即在已知观察结果是x的情况下,去推断环境参数θ。L是关于θ的函数。
,即在已知观察结果是x的情况下,去推断环境参数θ。L是关于θ的函数。
- 概率:
2.2、极大似然估计
2.2.1、简介
- 我们先用简单的抛硬币实验说明一下什么是极大似然估计。
- 假设,抛了10次硬币,7次人像朝上,3次数字朝上,这是实验的情况;设人像朝上的概率为θ,数字朝上的概率为1-θ,这是真实的情况。


- 我们要做的就是计算出θ的值。
- 我们根据假设出的θ,可以得出硬币抛出这种情况的概率为:
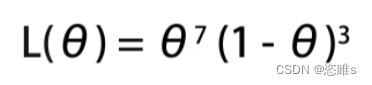 ,函数L(θ)被称为θ的似然函数,L(θ)的值被称为似然值。
,函数L(θ)被称为θ的似然函数,L(θ)的值被称为似然值。 - 我们可以枚举θ的值,然后画出L(θ)的图像。
 ,可以看出θ=0.7时,L(θ)的值最大,即硬币最有可能抛出上述情况。
,可以看出θ=0.7时,L(θ)的值最大,即硬币最有可能抛出上述情况。- 最大似然估计就是要求环境参数θ等于多少时,观测的结果最可能发生。
- 【注】理念情况下,θ应该为0.5,与计算的θ不符合。我们可以增加实验次数,例如抛1w次,重新进行计算。
2.2.2、作为损失函数
- 我们已经了解了极大似然估计,那接下来看看它是如何作为损失函数的呢。
- 我们还是用之前的这个案例。其中W和b是环境对应的参数,它确定了神经网络中概率模型的样子。这些输入的图片就像抛出的一个个硬币。
- 在这极大似然估计就是要求W,b等于多少时,观测的结果(输入图片的真实值)最可能发生。
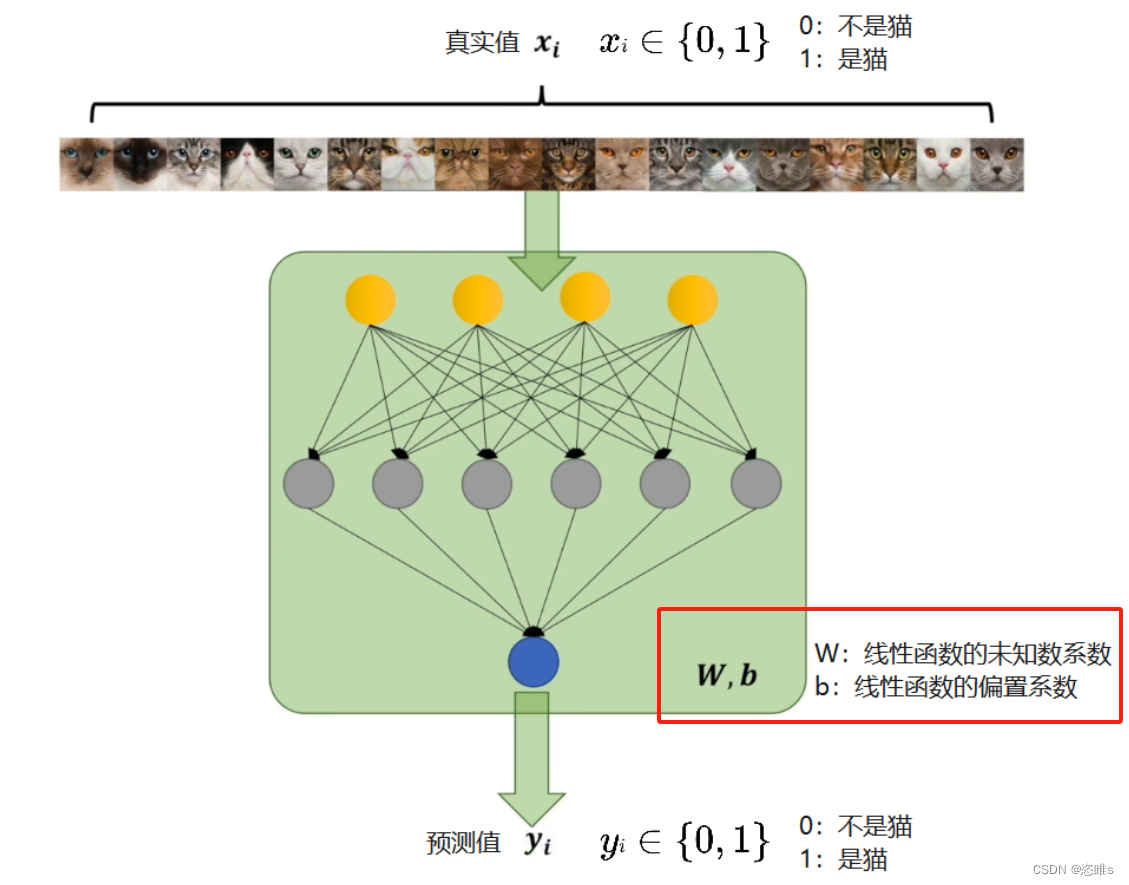
- 已知似然:
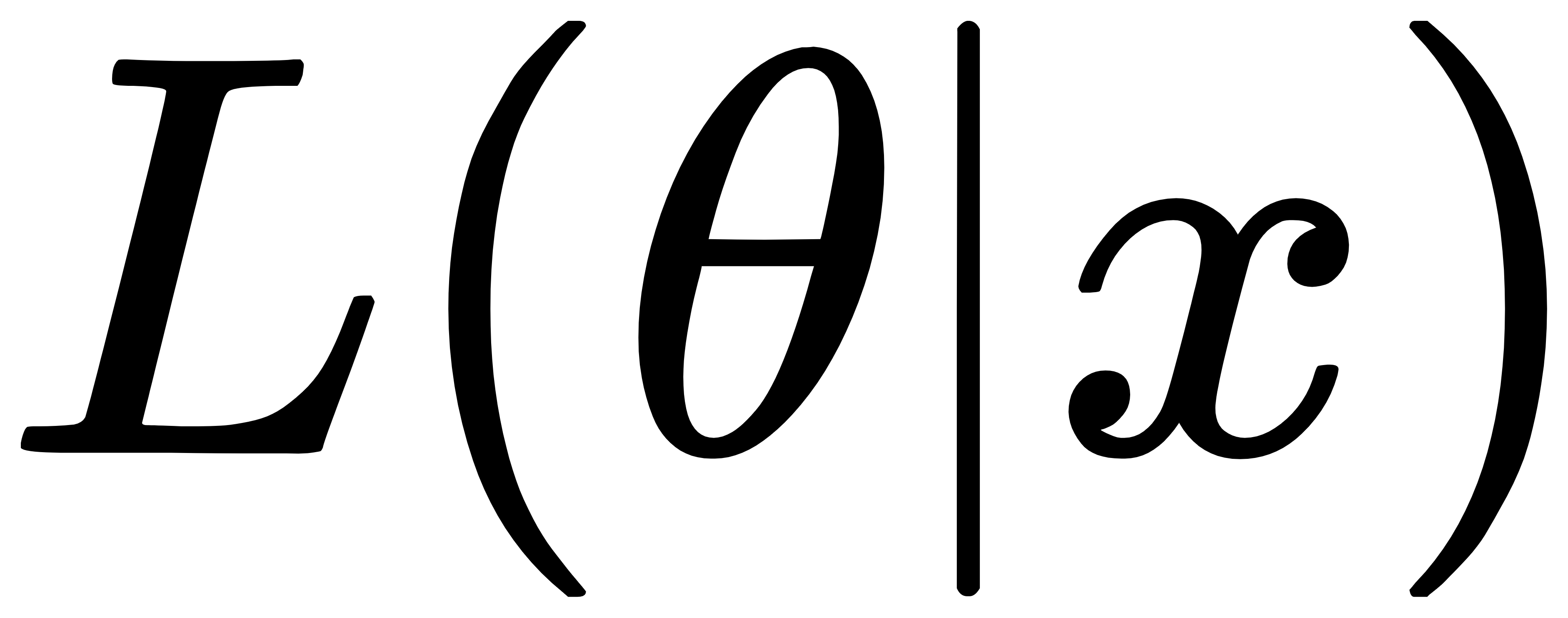 是在已知观察结果是x的情况下,去推断环境参数θ。对应到这里,得到似然函数为:
是在已知观察结果是x的情况下,去推断环境参数θ。对应到这里,得到似然函数为:
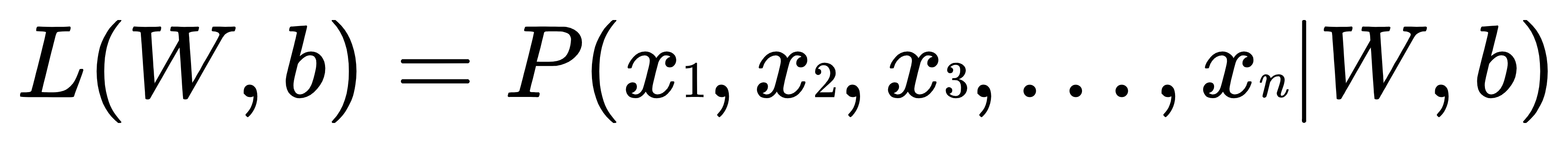 (W,b的情况下,
(W,b的情况下,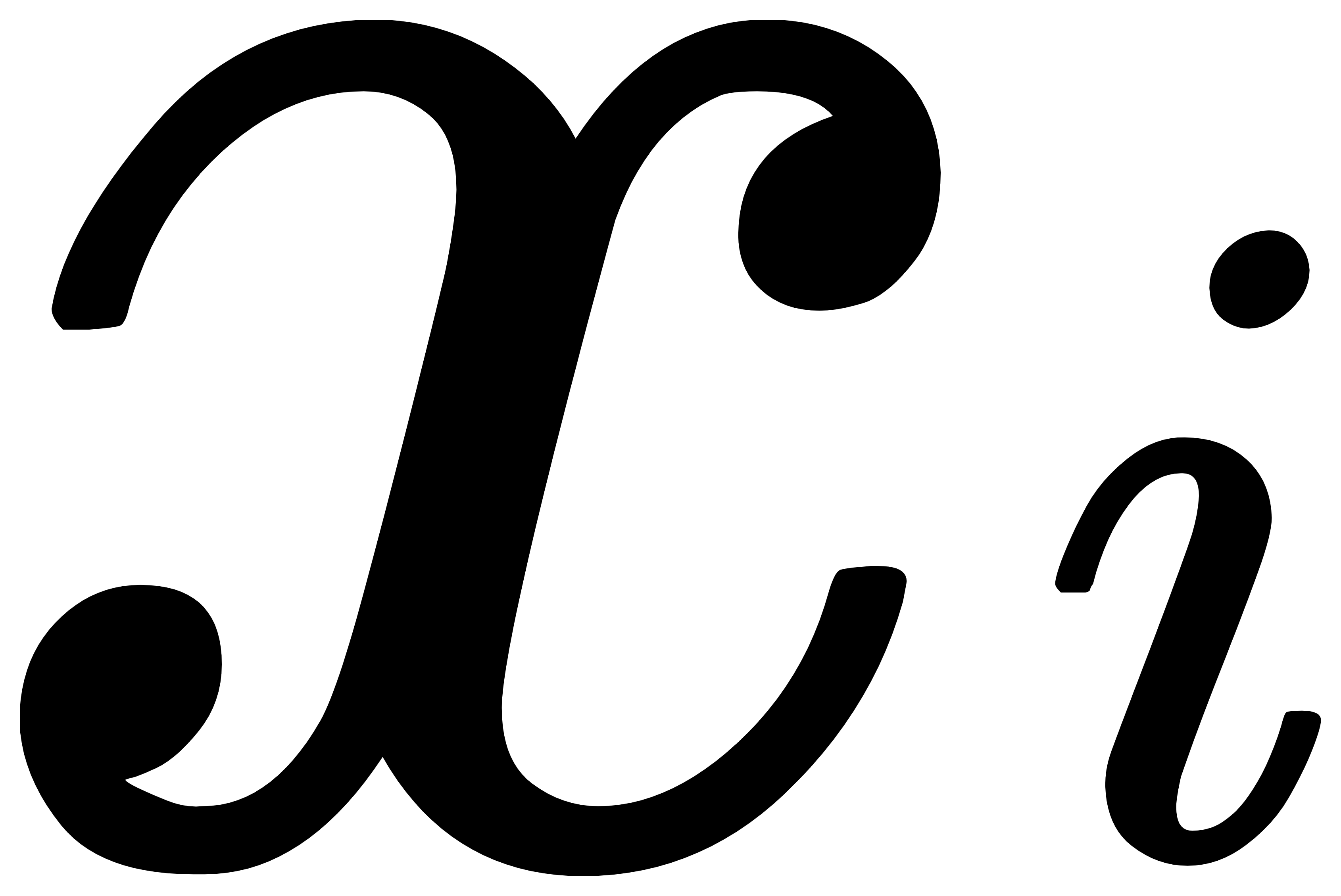 发生的概率)
发生的概率)
- 将似然函数写成连乘的形式:
- 由于W,b在神经网络中是确定值,而
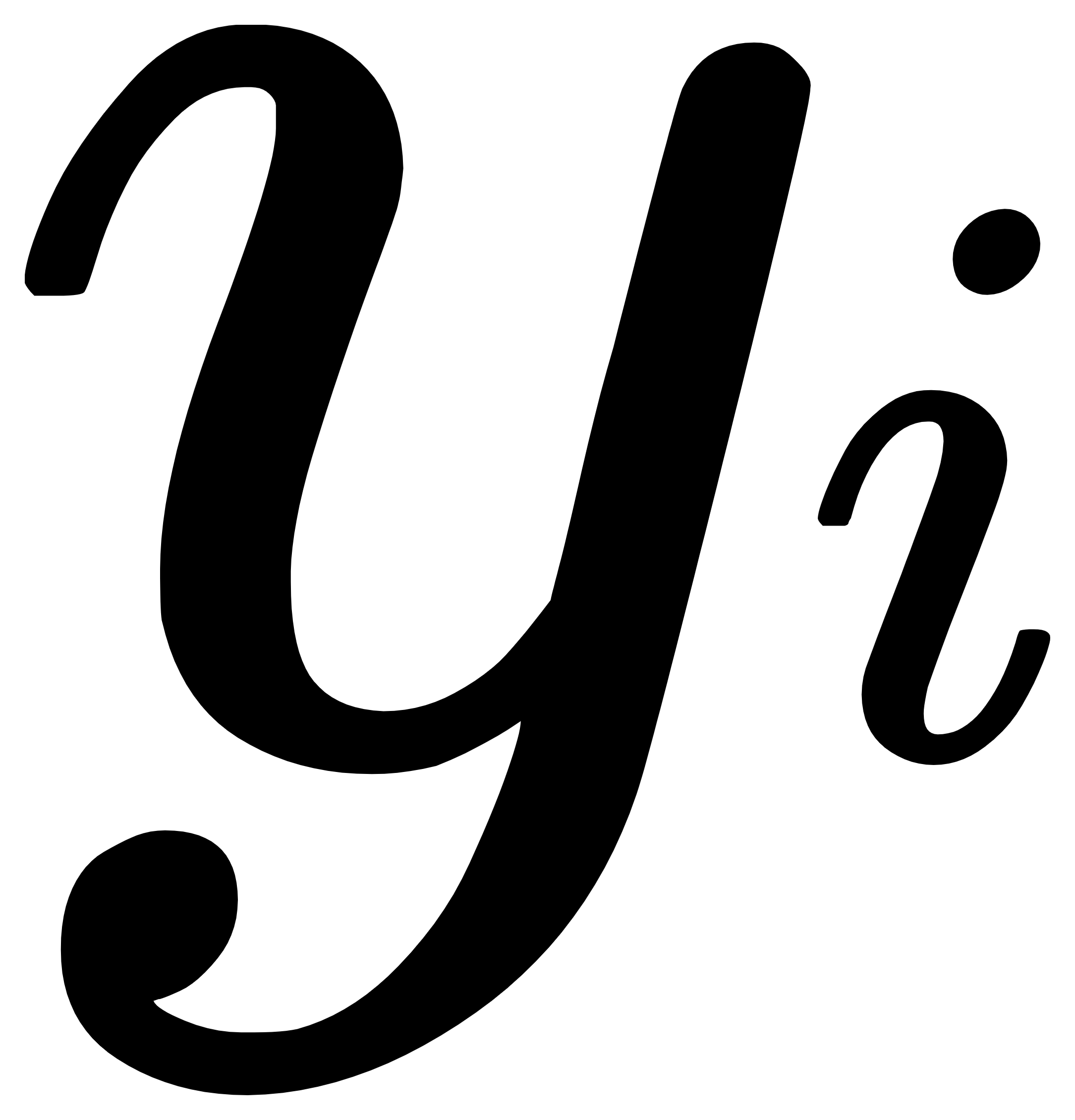 是由W,b得到的,所以可以使用
是由W,b得到的,所以可以使用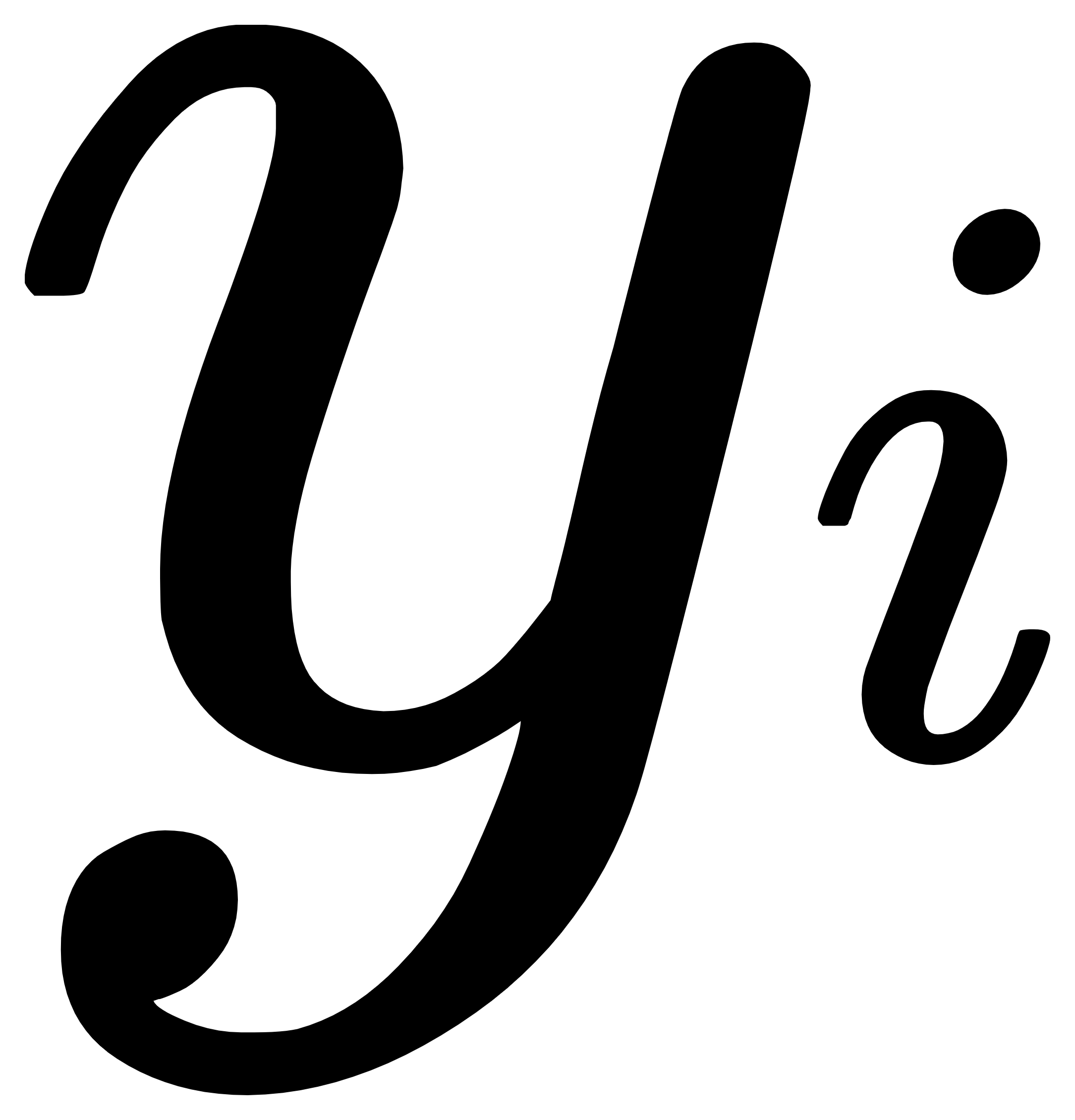 代替W,b,即:
代替W,b,即:
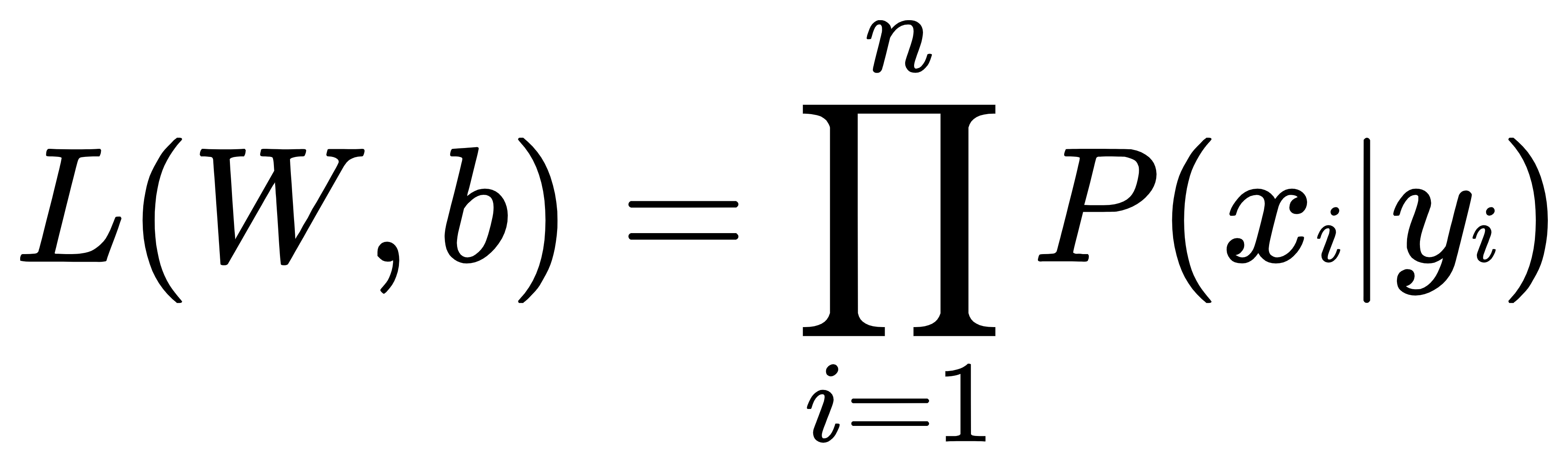 (W,b隐藏在
(W,b隐藏在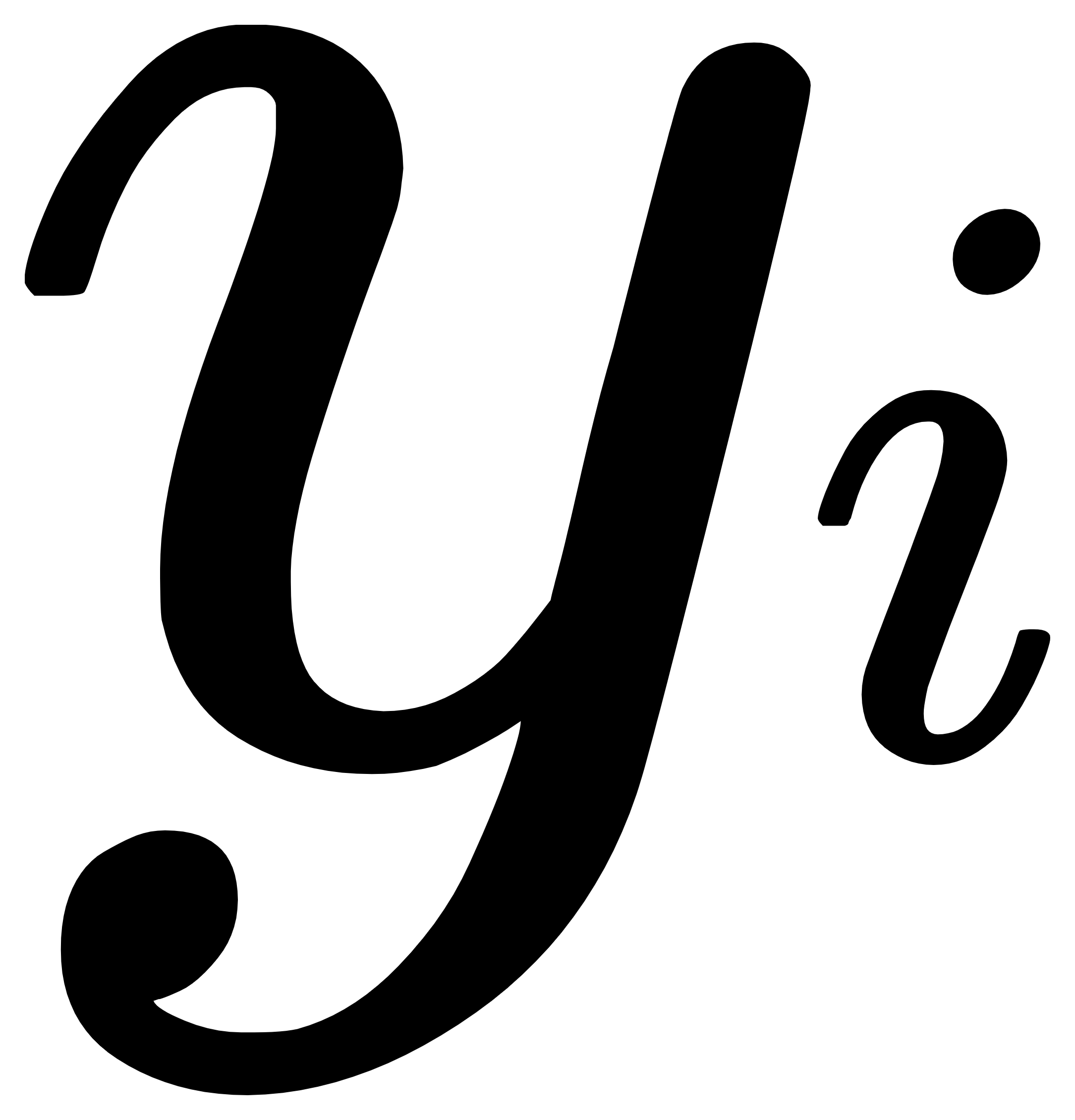 中)
中)
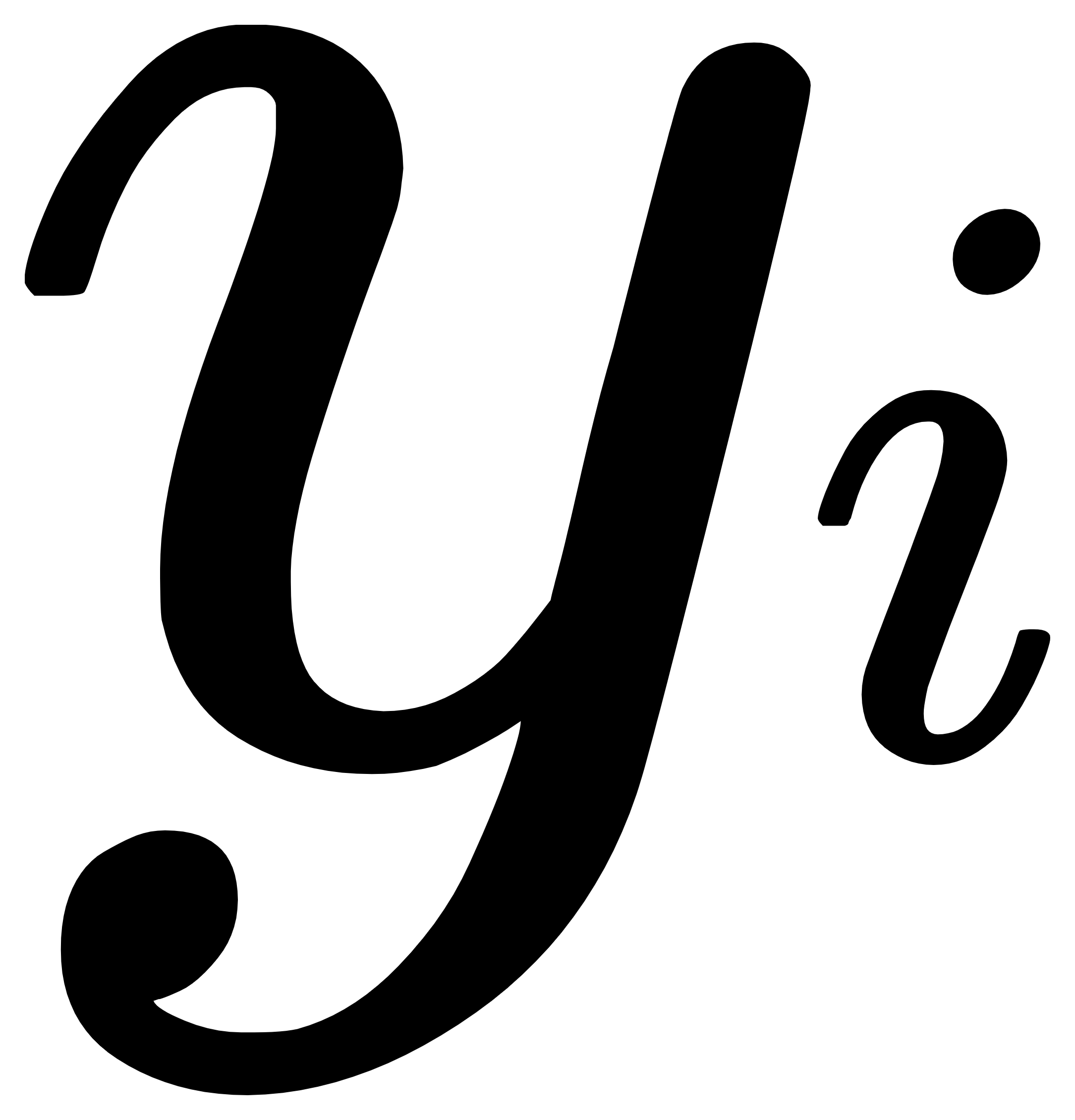 的概率是真实情况,
的概率是真实情况,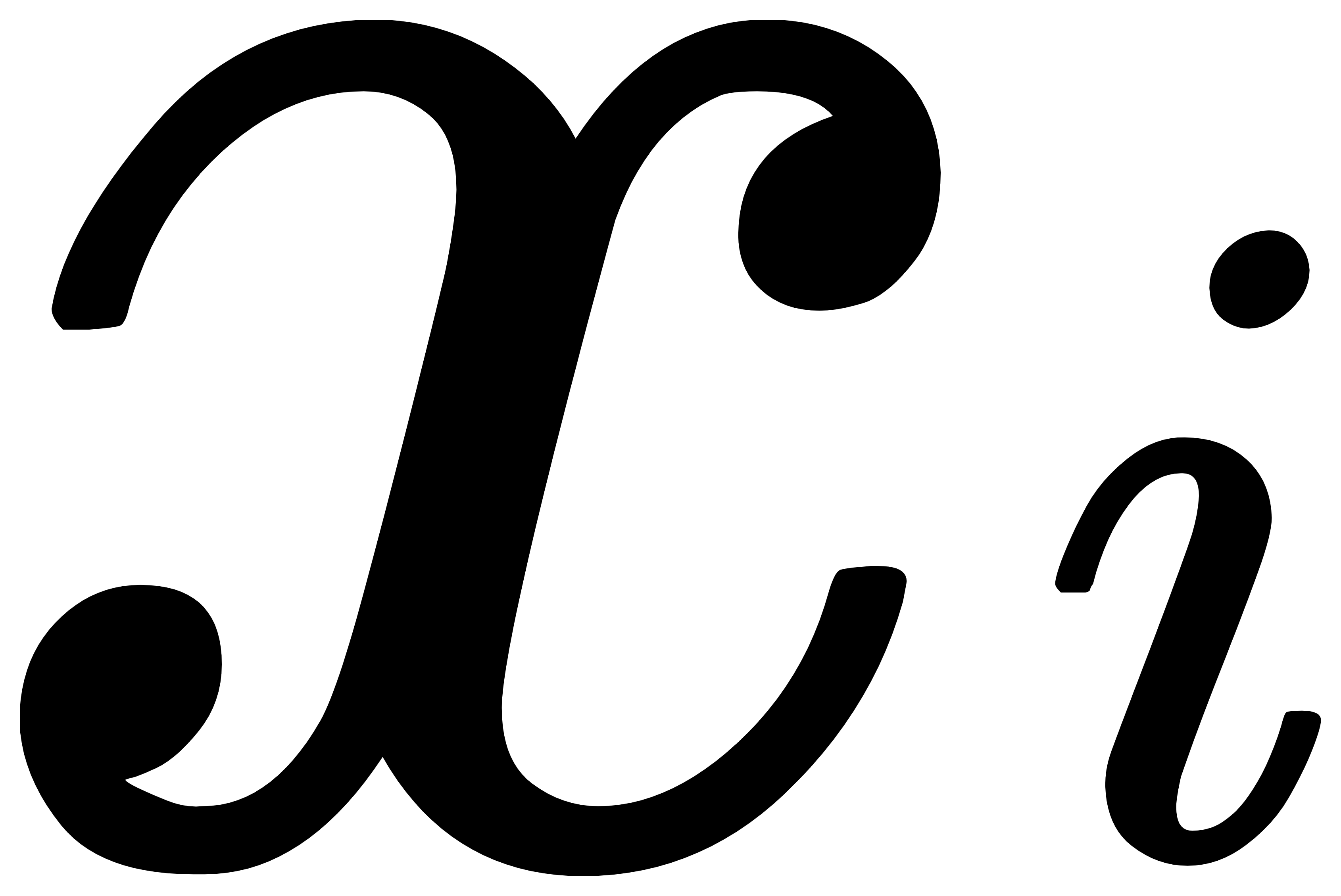 的概率是理念情况(需要不断逼近的情况)。
的概率是理念情况(需要不断逼近的情况)。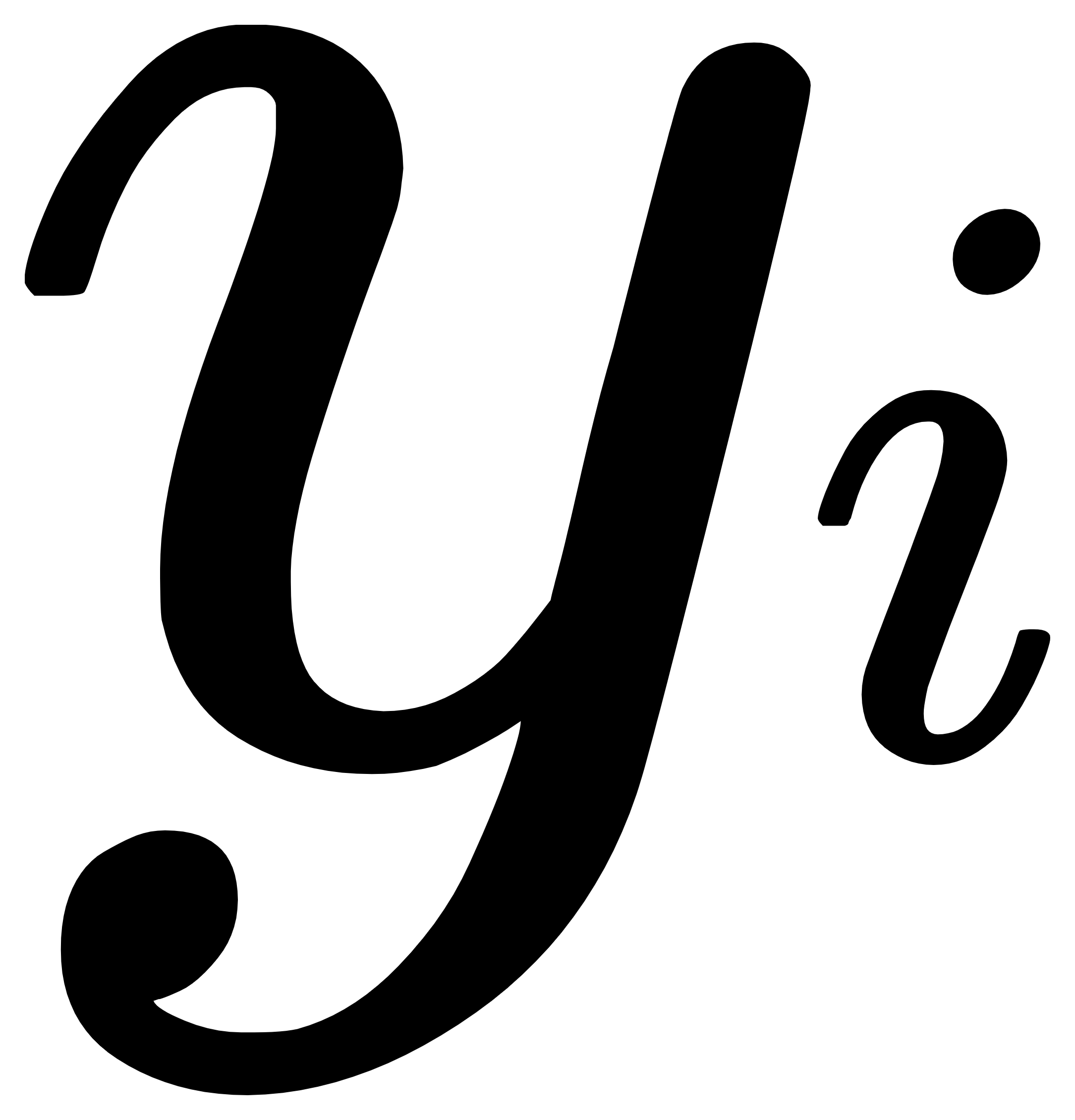 的概率就是我们需要不断调整的θ。
的概率就是我们需要不断调整的θ。- 我们再进行一次替换。由于
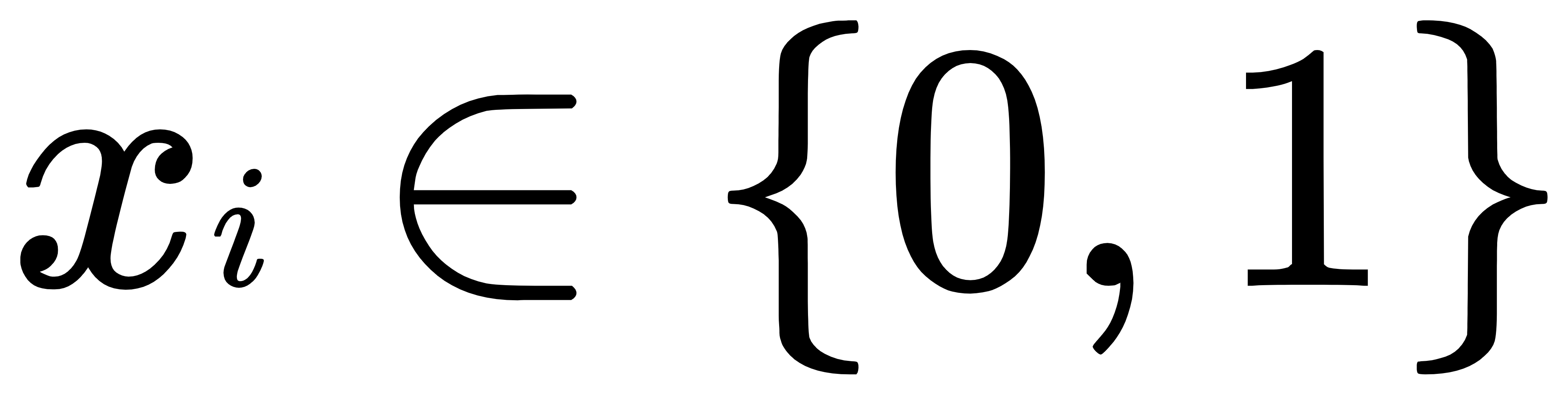 ,设
,设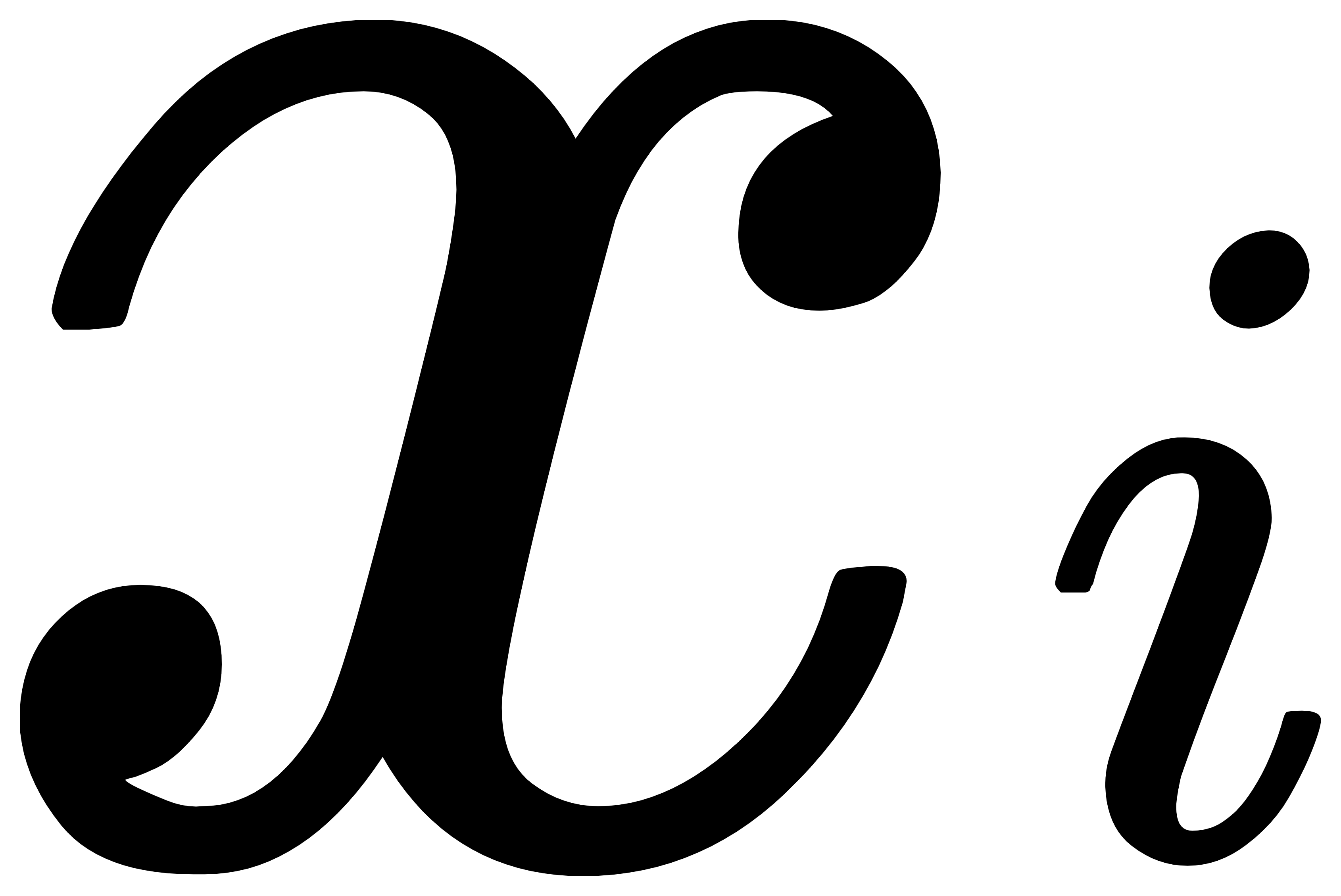 为1的概率为p,
为1的概率为p, 为0的概率为1-p,则
为0的概率为1-p,则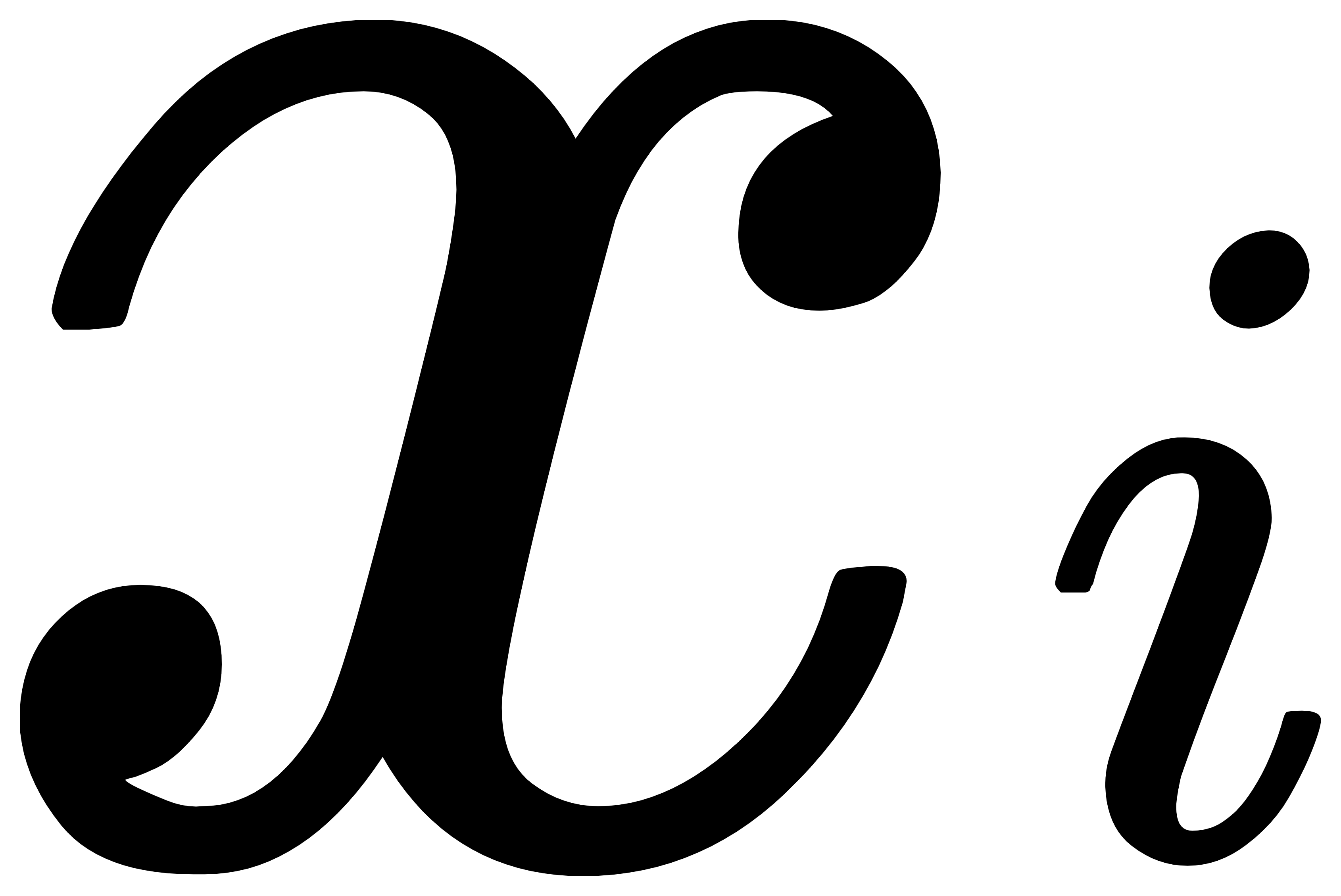 的概率分布为:
的概率分布为:
- 将
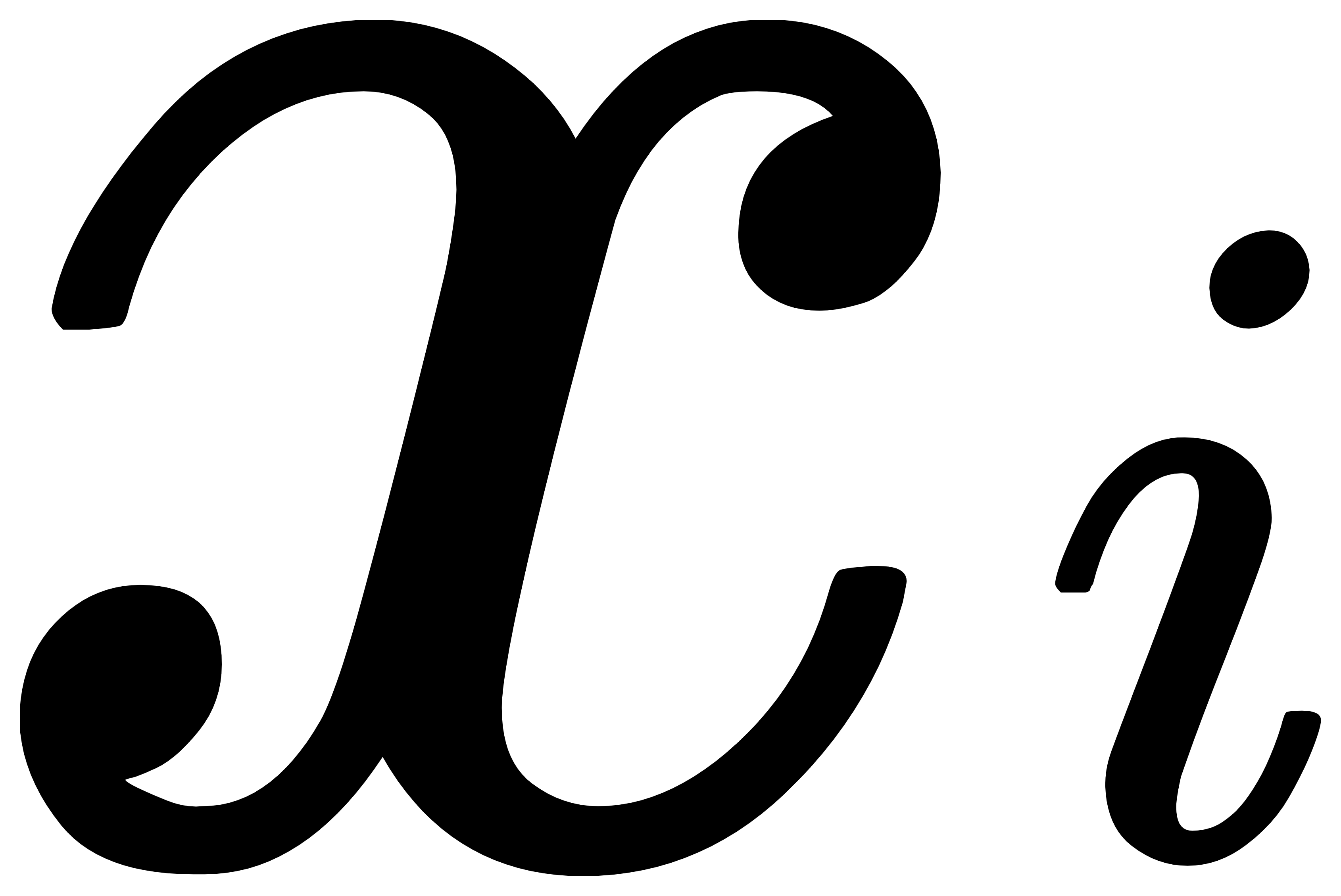 的概率改成
的概率改成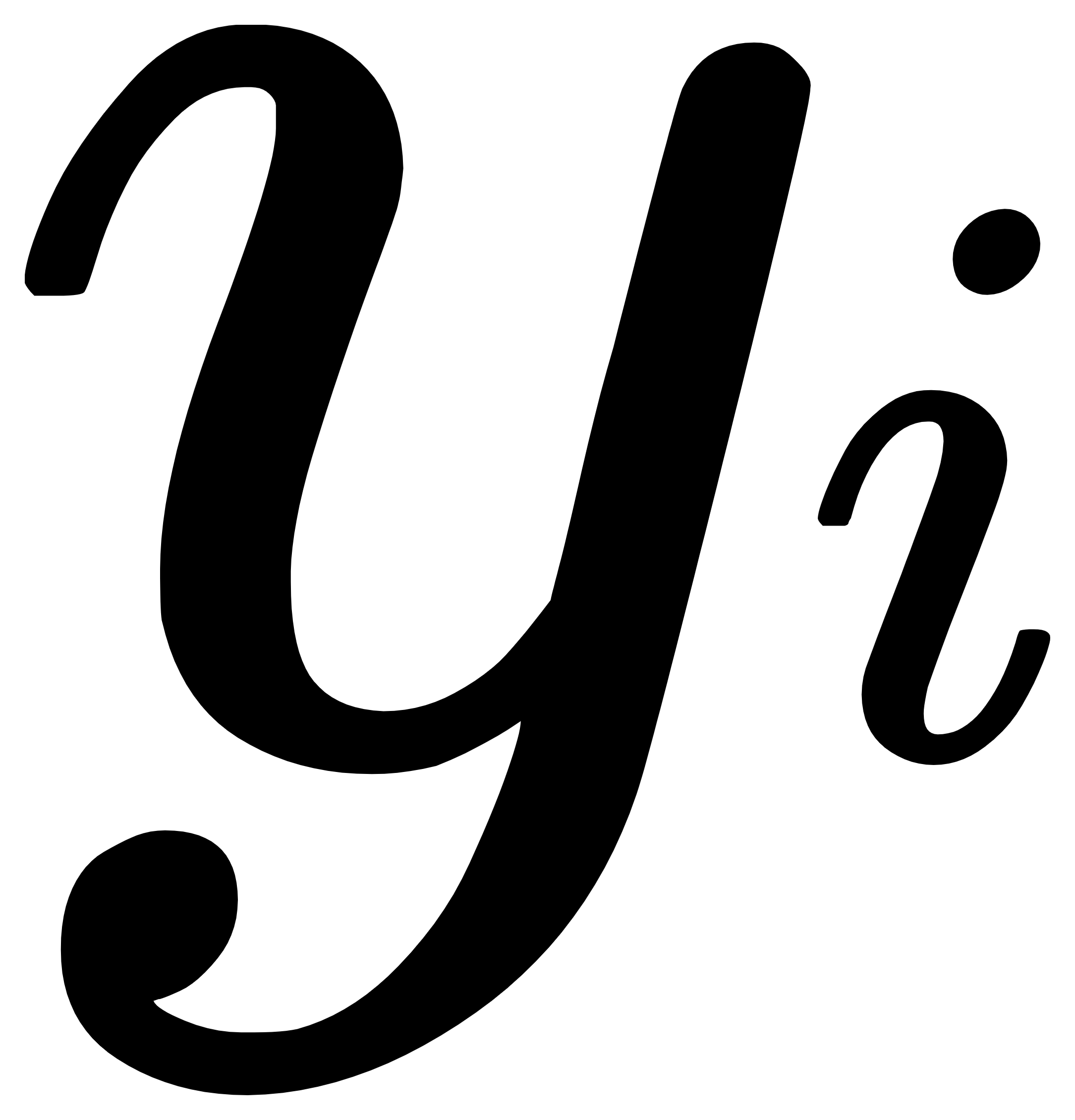 的概率,似然函数就可以替换成下面的形式:
的概率,似然函数就可以替换成下面的形式:
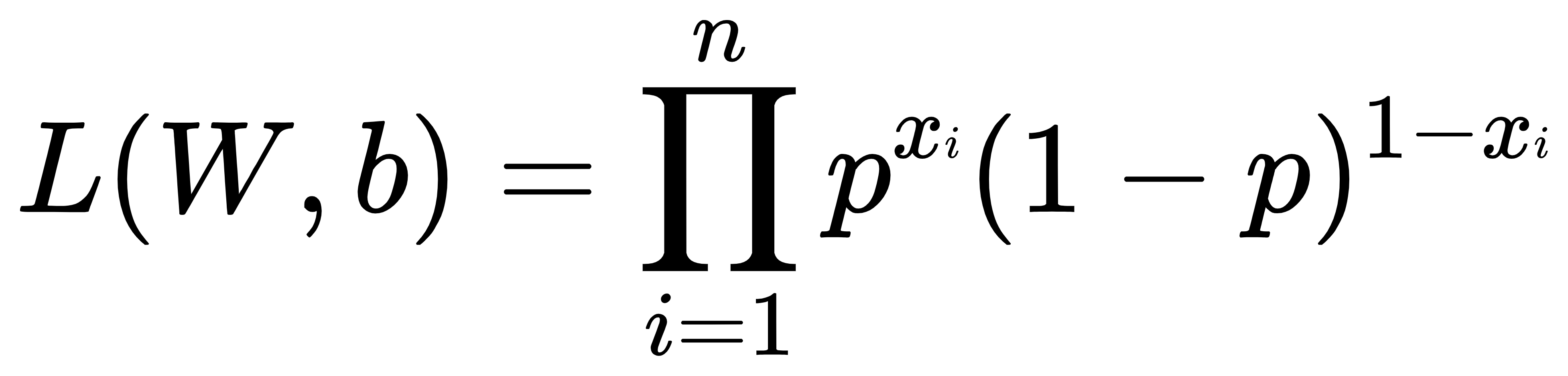 ,其中p为
,其中p为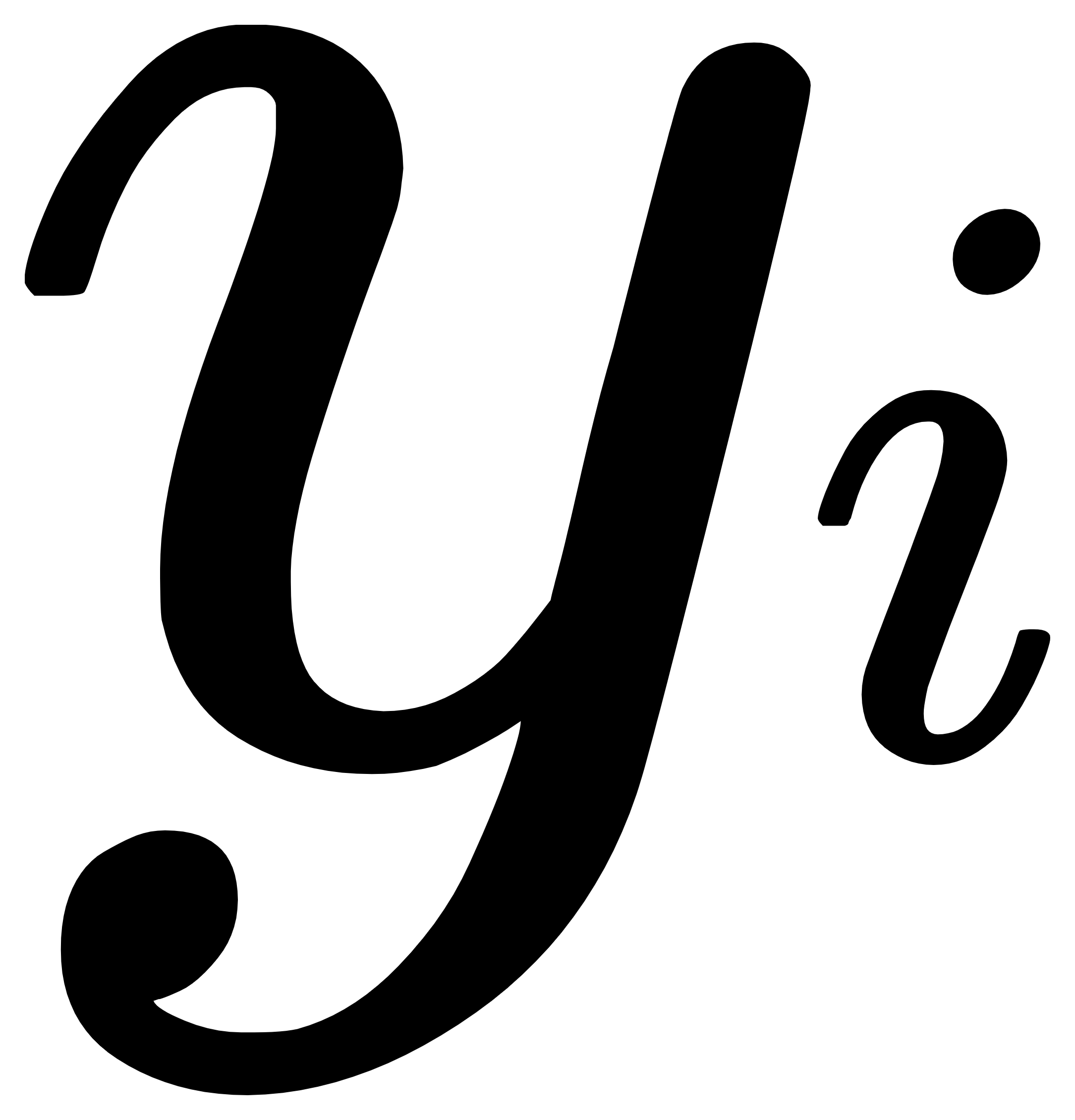 为1的概率。
为1的概率。
- 两边同时取对数,把连乘变成连加,进行化简。取对数不影响函数的单调性。
- 在这个公式基础上添加一个负号,将最大化该公式改为最小化,这就符合损失函数的定义了。即:
3、总结
- 训练神经网络其实就是要找到适合的W和b。而
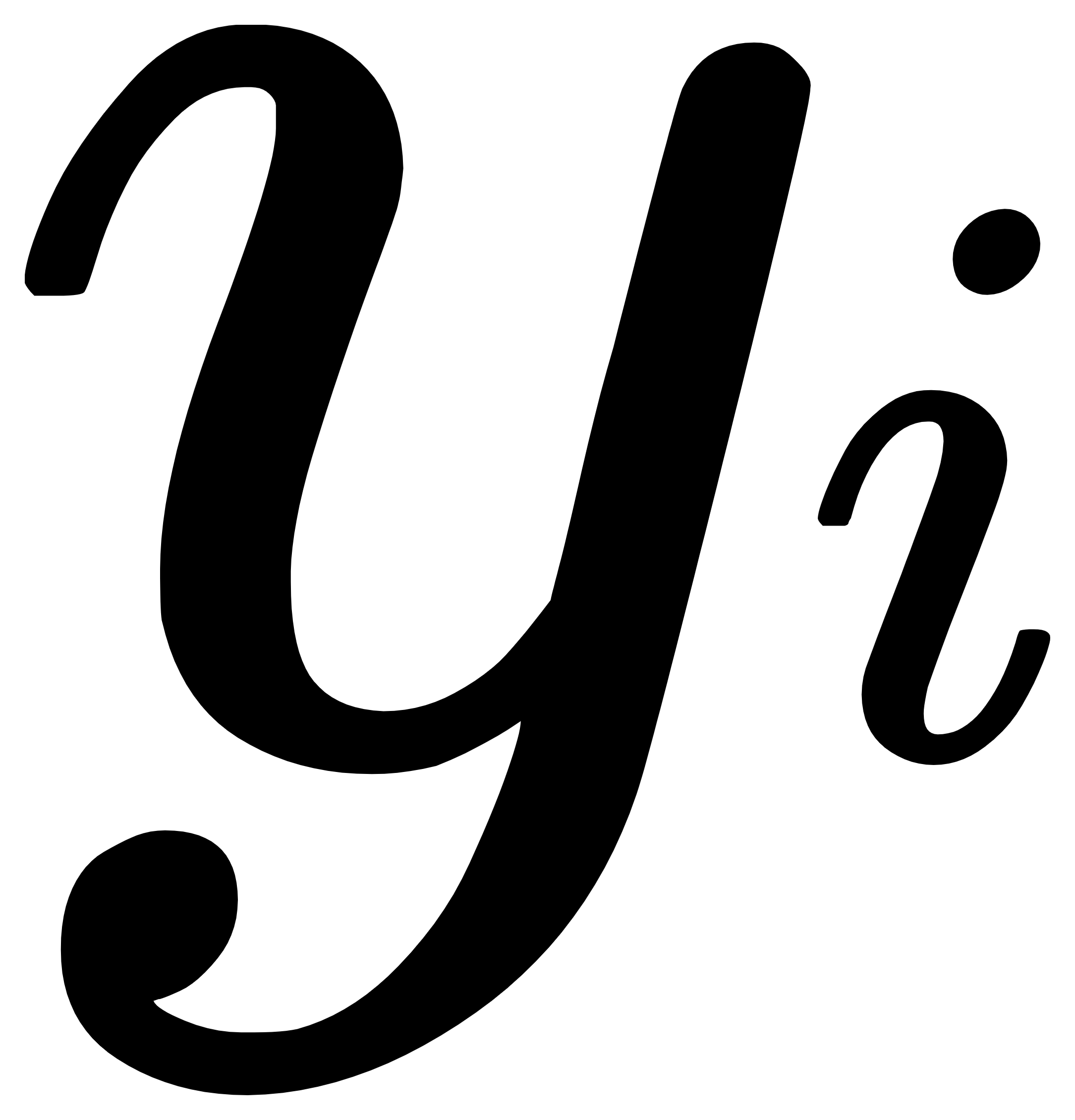 是现在W和b的产物,我们可以根据
是现在W和b的产物,我们可以根据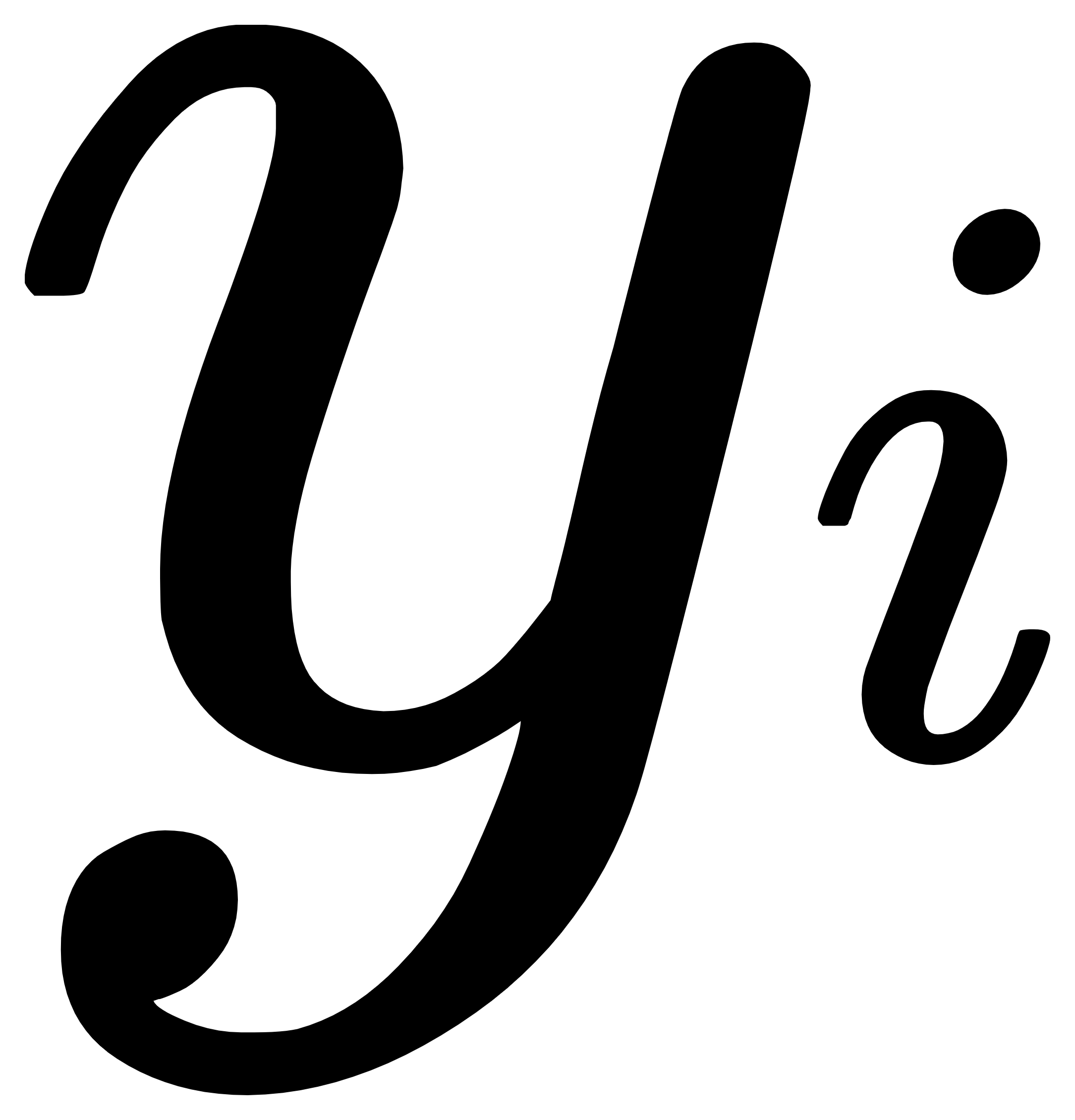 的概率得到现有模型和理想模型的差距。当我们在最大化似然函数的时候,就是要求W,b等于多少时,观测的结果(输入图片的真实值)最可能发生,而这里的W,b只是改成了
的概率得到现有模型和理想模型的差距。当我们在最大化似然函数的时候,就是要求W,b等于多少时,观测的结果(输入图片的真实值)最可能发生,而这里的W,b只是改成了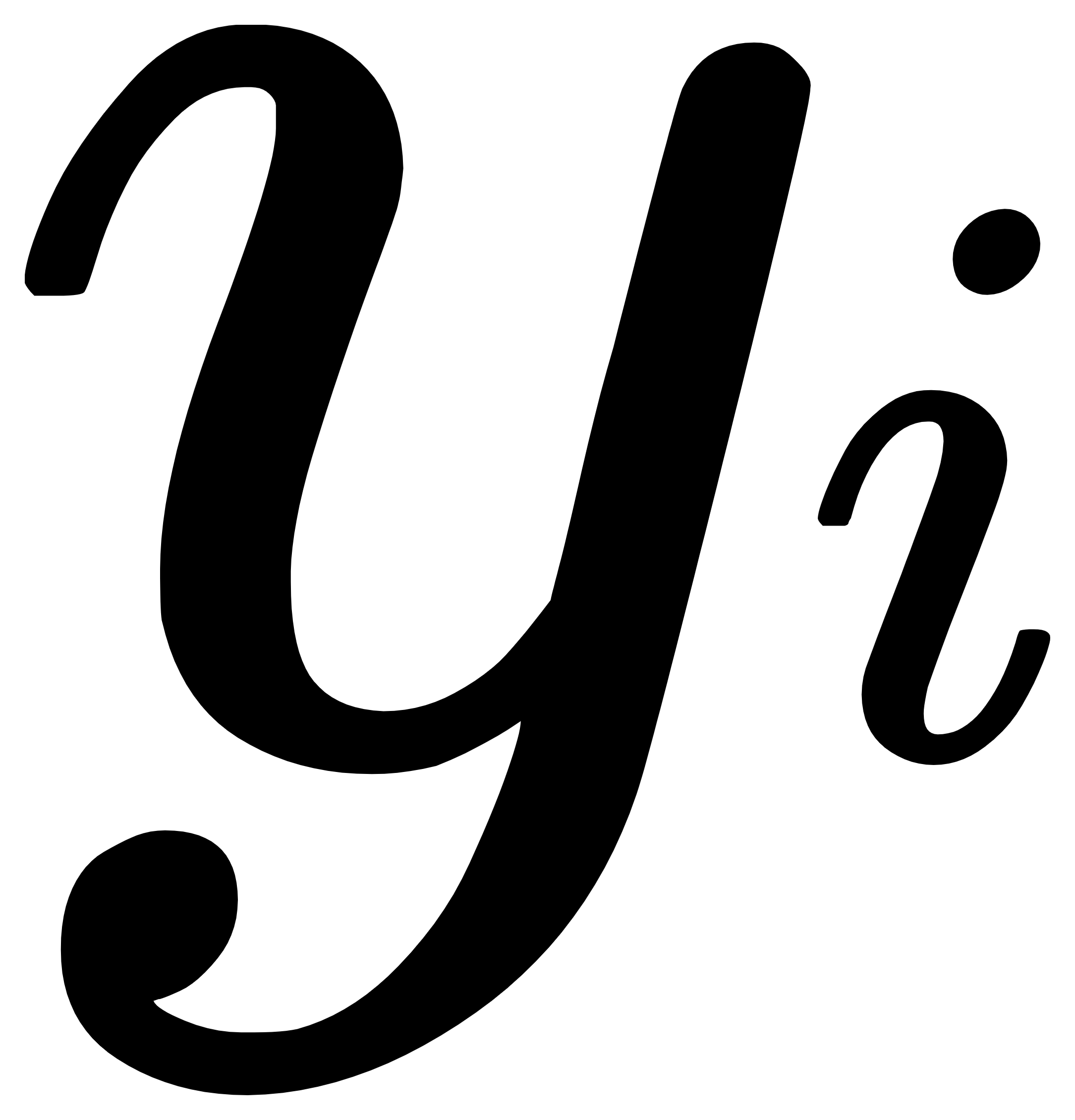 的概率。
的概率。