PRT(Precomputed Radiance Transfer【2002】)原理实现

news2024/9/28 23:33:38

声明

本文源自对Games202课程，作业2的总结。

参考

  1. 手把手教你写GAMES202作业：GAMES202-作业2： Precomputed Radiance Transfer（球谐函数）
  2. GAMES 202 作业2
  3. Games202课程
  4. 个人Blog 课程总结：Games202(P6、P7)环境光照与PRT全局光照

实现目标

实现材质为Diffuse的，基于球谐函数的PRT预处理。
分别实现无阴影、有阴影、有多次光线弹射的预处理。

注意：

  • 材质类型为Diffuse，不考虑Glossy的物体

文章目录

  • 声明
  • 参考
  • 实现目标
  • 一、架构基础
    • --需要提供光线追踪算法--
    • --需要提供球谐函数基函数--
      • 1. 使用硬编码
      • 2. 公式求解基函数
  • 二、预计算核心算法实现
    • 1. 预计算环境光
    • 2. 预计算传输项球谐函数
      • 无阴影函数
      • 有阴影函数
      • 有阴影且多次反射函数
    • 3. 保存计算得到的L和T的球谐系数
  • 三、使用预计算数据进行渲染
  • 四、基于漫反射材质的PRT总结
    • 什么时候会用到快速的场景切换呢？
    • 与光照烘培的区别
  • 五、基于Glossy物体的PRT
  • 六、游戏界环境是否使用PRT来做全局光照
    • 那我们就没必要学习吗？？

一、架构基础

–需要提供光线追踪算法–

需要实现函数：
光线与物体是否相交：scene->rayIntersect(Ray3f ray)
光线与物体相交信息：scene->rayIntersect(Ray3f ray,Intersection its)

–需要提供球谐函数基函数–

1. 使用硬编码

保存前4阶，共16个球谐基函数。

		double HardcodedSH00(const Eigen::Vector3d& d) {
			// 0.5 * sqrt(1/pi)
			return 0.282095;
		}

		double HardcodedSH1n1(const Eigen::Vector3d& d) {
			// -sqrt(3/(4pi)) * y
			return -0.488603 * d.y();
		}

		double HardcodedSH10(const Eigen::Vector3d& d) {
			// sqrt(3/(4pi)) * z
			return 0.488603 * d.z();
		}

		double HardcodedSH1p1(const Eigen::Vector3d& d) {
			// -sqrt(3/(4pi)) * x
			return -0.488603 * d.x();
		}

		double HardcodedSH2n2(const Eigen::Vector3d& d) {
			// 0.5 * sqrt(15/pi) * x * y
			return 1.092548 * d.x() * d.y();
		}

		double HardcodedSH2n1(const Eigen::Vector3d& d) {
			// -0.5 * sqrt(15/pi) * y * z
			return -1.092548 * d.y() * d.z();
		}

		double HardcodedSH20(const Eigen::Vector3d& d) {
			// 0.25 * sqrt(5/pi) * (-x^2-y^2+2z^2)
			return 0.315392 * (-d.x() * d.x() - d.y() * d.y() + 2.0 * d.z() * d.z());
		}

		double HardcodedSH2p1(const Eigen::Vector3d& d) {
			// -0.5 * sqrt(15/pi) * x * z
			return -1.092548 * d.x() * d.z();
		}

		double HardcodedSH2p2(const Eigen::Vector3d& d) {
			// 0.25 * sqrt(15/pi) * (x^2 - y^2)
			return 0.546274 * (d.x() * d.x() - d.y() * d.y());
		}

		double HardcodedSH3n3(const Eigen::Vector3d& d) {
			// -0.25 * sqrt(35/(2pi)) * y * (3x^2 - y^2)
			return -0.590044 * d.y() * (3.0 * d.x() * d.x() - d.y() * d.y());
		}

		double HardcodedSH3n2(const Eigen::Vector3d& d) {
			// 0.5 * sqrt(105/pi) * x * y * z
			return 2.890611 * d.x() * d.y() * d.z();
		}

		double HardcodedSH3n1(const Eigen::Vector3d& d) {
			// -0.25 * sqrt(21/(2pi)) * y * (4z^2-x^2-y^2)
			return -0.457046 * d.y() * (4.0 * d.z() * d.z() - d.x() * d.x()
				- d.y() * d.y());
		}

		double HardcodedSH30(const Eigen::Vector3d& d) {
			// 0.25 * sqrt(7/pi) * z * (2z^2 - 3x^2 - 3y^2)
			return 0.373176 * d.z() * (2.0 * d.z() * d.z() - 3.0 * d.x() * d.x()
				- 3.0 * d.y() * d.y());
		}

		double HardcodedSH3p1(const Eigen::Vector3d& d) {
			// -0.25 * sqrt(21/(2pi)) * x * (4z^2-x^2-y^2)
			return -0.457046 * d.x() * (4.0 * d.z() * d.z() - d.x() * d.x()
				- d.y() * d.y());
		}

		double HardcodedSH3p2(const Eigen::Vector3d& d) {
			// 0.25 * sqrt(105/pi) * z * (x^2 - y^2)
			return 1.445306 * d.z() * (d.x() * d.x() - d.y() * d.y());
		}

		double HardcodedSH3p3(const Eigen::Vector3d& d) {
			// -0.25 * sqrt(35/(2pi)) * x * (x^2-3y^2)
			return -0.590044 * d.x() * (d.x() * d.x() - 3.0 * d.y() * d.y());
		}

		double HardcodedSH4n4(const Eigen::Vector3d& d) {
			// 0.75 * sqrt(35/pi) * x * y * (x^2-y^2)
			return 2.503343 * d.x() * d.y() * (d.x() * d.x() - d.y() * d.y());
		}

		double HardcodedSH4n3(const Eigen::Vector3d& d) {
			// -0.75 * sqrt(35/(2pi)) * y * z * (3x^2-y^2)
			return -1.770131 * d.y() * d.z() * (3.0 * d.x() * d.x() - d.y() * d.y());
		}

		double HardcodedSH4n2(const Eigen::Vector3d& d) {
			// 0.75 * sqrt(5/pi) * x * y * (7z^2-1)
			return 0.946175 * d.x() * d.y() * (7.0 * d.z() * d.z() - 1.0);
		}

		double HardcodedSH4n1(const Eigen::Vector3d& d) {
			// -0.75 * sqrt(5/(2pi)) * y * z * (7z^2-3)
			return -0.669047 * d.y() * d.z() * (7.0 * d.z() * d.z() - 3.0);
		}

		double HardcodedSH40(const Eigen::Vector3d& d) {
			// 3/16 * sqrt(1/pi) * (35z^4-30z^2+3)
			double z2 = d.z() * d.z();
			return 0.105786 * (35.0 * z2 * z2 - 30.0 * z2 + 3.0);
		}

		double HardcodedSH4p1(const Eigen::Vector3d& d) {
			// -0.75 * sqrt(5/(2pi)) * x * z * (7z^2-3)
			return -0.669047 * d.x() * d.z() * (7.0 * d.z() * d.z() - 3.0);
		}

		double HardcodedSH4p2(const Eigen::Vector3d& d) {
			// 3/8 * sqrt(5/pi) * (x^2 - y^2) * (7z^2 - 1)
			return 0.473087 * (d.x() * d.x() - d.y() * d.y())
				* (7.0 * d.z() * d.z() - 1.0);
		}

		double HardcodedSH4p3(const Eigen::Vector3d& d) {
			// -0.75 * sqrt(35/(2pi)) * x * z * (x^2 - 3y^2)
			return -1.770131 * d.x() * d.z() * (d.x() * d.x() - 3.0 * d.y() * d.y());
		}

		double HardcodedSH4p4(const Eigen::Vector3d& d) {
			// 3/16*sqrt(35/pi) * (x^2 * (x^2 - 3y^2) - y^2 * (3x^2 - y^2))
			double x2 = d.x() * d.x();
			double y2 = d.y() * d.y();
			return 0.625836 * (x2 * (x2 - 3.0 * y2) - y2 * (3.0 * x2 - y2));
		}

2. 公式求解基函数

当阶数较大时，无法使用硬编码编写，则需要使用公式直接计算。

  1. 首先根据球谐函数定义，有：
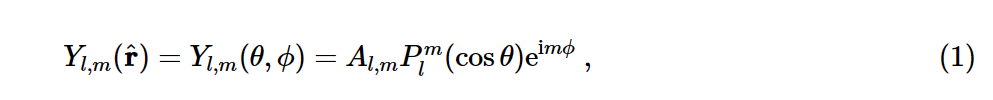
    在这里插入图片描述

  2. 得到 A l m A_l^m Alm​ (归一化系数)
    在这里插入图片描述

double kml = sqrt(
			(2.0 * l + 1) * Factorial(l - abs(m)) /
			(4.0 * M_PI * Factorial(l + abs(m)))
			);
  1. 求解 P l m ( c o s θ ) P_l^m(cos\theta) Plm​(cosθ)，根据球谐函数如下性质，求得 c o s θ cos\theta cosθ 在任意基函数的值
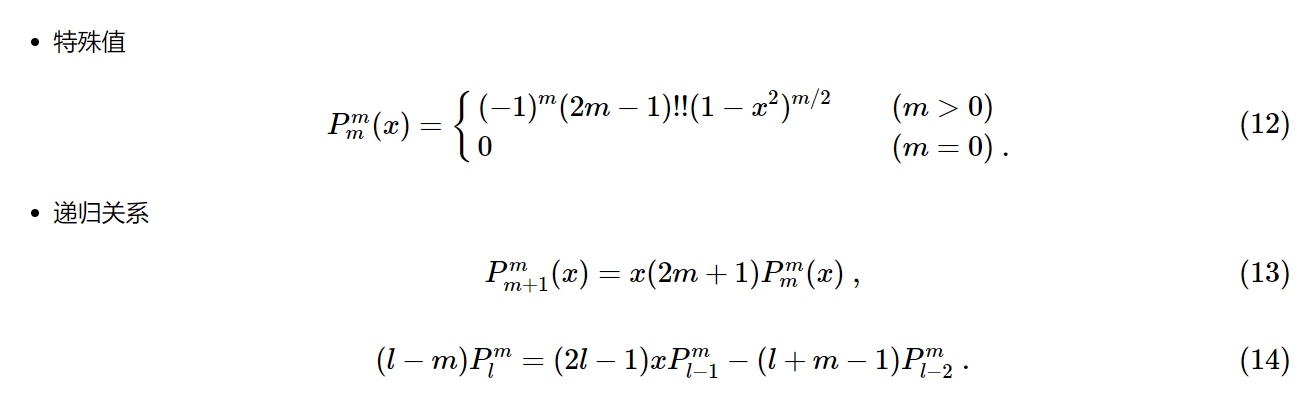
    在这里插入图片描述
    注：
    -. 当 P m m ( x ) P_m^m(x) Pmm​(x) 中 m = 0 m=0 m=0时，值为1，不是0！（这里公式错了）
    -. 因为基函数可以不需要求解 ( − 1 ) m (-1)^m (−1)m （系数的正负可以替代），所以在一些表达式中无正负号。
double EvalLegendrePolynomial(int l, int m, double x) {
	// Compute Pmm(x) = (-1)^m(2m - 1)!!(1 - x^2)^(m/2), where !! is the double factorial.
	double pmm = 1.0;
	// P00 is defined as 1.0, do don't evaluate Pmm unless we know m > 0
	if (m > 0) {
		double sign = (m % 2 == 0 ? 1 : -1);
		pmm = sign * DoubleFactorial(2 * m - 1) * pow(1 - x * x, m / 2.0);
	}

	if (l == m) {
		// Pml is the same as Pmm so there's no lifting to higher bands needed
		return pmm;
	}

	// Compute Pmm+1(x) = x(2m + 1)Pmm(x)
	double pmm1 = x * (2 * m + 1) * pmm;
	if (l == m + 1) {
		// Pml is the same as Pmm+1 so we are done as well
		return pmm1;
	}

	// Use the last two computed bands to lift up to the next band until l is
	// reached, using the recurrence relationship:
	// Pml(x) = (x(2l - 1)Pml-1 - (l + m - 1)Pml-2) / (l - m)
	for (int n = m + 2; n <= l; n++) {
		double pmn = (x * (2 * n - 1) * pmm1 - (n + m - 1) * pmm) / (n - m);
		pmm = pmm1;
		pmm1 = pmn;
	}
	// Pmm1 at the end of the above loop is equal to Pml
	return pmm1;
}

当 m < 0 m<0 m<0时,根据对称性质
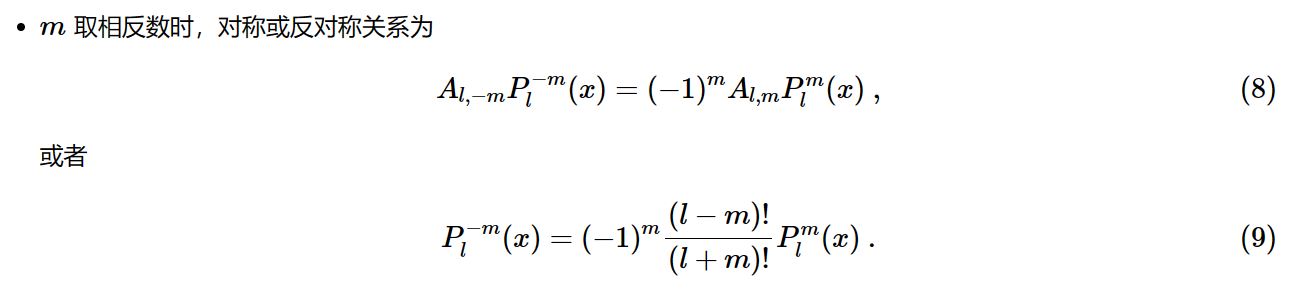
在这里插入图片描述
即：偶数取反，奇数不变。（因为基函数可以不考虑符号正负，故可以认为如下等式成立） P l − m = P l m P_l^{-m} = P_l^m Pl−m​=Plm​

  1. 求解 e i m ϕ = c o s ( m ϕ ) + i ⋅ s i n ( m ϕ ) e^{im\phi} = cos(m\phi) + i·sin(m\phi) eimϕ=cos(mϕ)+i⋅sin(mϕ)。【为什么乘以 2 \sqrt 2 2 ​，网上没有找到证明，但是确实乘以 2 \sqrt 2 2 ​才能得到正确结果！】

    • 当m>0时， e i m ϕ = 2 ∗ c o s ( m ϕ ) e^{im\phi} = \sqrt{2} * cos(m\phi) eimϕ=2 ​∗cos(mϕ)
    • 当m<0时， e i m ϕ = 2 ∗ s i n ( − m ϕ ) e^{im\phi} = \sqrt{2} * sin(-m\phi) eimϕ=2 ​∗sin(−mϕ)
    • 当m=0时， e i m ϕ = 1 e^{im\phi} = 1 eimϕ=1

综上得出最终代码：

if (m > 0) {
	return kml *  sqrt(2.0) * cos(m * phi) *
		EvalLegendrePolynomial(l, m, cos(theta));
}
else if (m < 0) {
	return kml * sqrt(2.0) * sin(-m * phi) *
		EvalLegendrePolynomial(l, -m, cos(theta));
}
else {
	return kml * EvalLegendrePolynomial(l, 0, cos(theta));
}

二、预计算核心算法实现

1. 预计算环境光

S H 系 数 ( l , m ) = ∑ i s a m p l e N u m L e ( i ) ∗ S H 基函 数 ( l , m ) ( D i r ( i ) ) ∗ d A SH系数_{(l,m)} = \sum_i^{sampleNum} Le(i) * SH基函数_{(l,m)}(Dir(i)) * dA SH系数(l,m)​=i∑sampleNum​Le(i)∗SH基函数(l,m)​(Dir(i))∗dA
其中：

  • ∑ i s a m p l e N u m = ∑ 天空盒 k 6 ∑ y h e i g h t ∑ x w e i g h t \sum_i^{sampleNum} = \sum_{天空盒k}^6 \sum_y^{height} \sum_x^{weight} ∑isampleNum​=∑天空盒k6​∑yheight​∑xweight​
  • i i i 为采样像素点
  • D i r ( i ) Dir(i) Dir(i)为该像素的方向向量
  • d A dA dA 为像素立体角

其中 计算Cubemap的一个像素对应的立体角的大小原理可参照
Solid Angle of A Cubemap Texel - 计算Cubemap的一个像素对应的立体角的大小

// 计算球谐系数
float sumWeight = 0;
for (int i = 0; i < 6; i++)
{
    for (int y = 0; y < height; y++)
    {
        for (int x = 0; x < width; x++)
        {
            // TODO: 此处你需要计算每个像素下cubemap某个面的球谐系数
            // 方向 
            Eigen::Vector3f dir = cubemapDirs[i * width * height + y * width + x];
            // 入射光
            int index = (y * width + x) * channel;
            Eigen::Array3f Le(images[i][index + 0], images[i][index + 1],
                              images[i][index + 2]);
            // 立体角
            float dA = CalcArea(x, y, width, height);
            
            // 计算球谐系数
            for (int l = 0; l <= SHOrder; l++) {
                for (int m = -l; m <= l; m++) {
                    // Eigen库不能在Vector3d，Vector3f之间相互赋值
                    double basic_fun_value = sh::EvalSHSlow(l, m, Eigen::Vector3d(dir.x(), dir.y(), dir.z()).normalized());
                    SHCoeffiecents[sh::GetIndex(l, m)] += Le * basic_fun_value * dA;
                }
            }
        }
    }
}
return SHCoeffiecents;

2. 预计算传输项球谐函数

∫ Ω V ( i ) B R D F ( i , o ) m a x ( n ⋅ w i , 0 ) d i \int_{\Omega}\quad V(i)\quad BRDF(i,o) \quad max(n\cdot w_i,0)\quad di ∫Ω​V(i)BRDF(i,o)max(n⋅wi​,0)di
注意：若材质为Diffuse，则 B R D F ( i , 0 ) = 1 / π BRDF(i,0)=1/\pi BRDF(i,0)=1/π;

将函数展开到球谐函数上，函数有：

  • 无阴影函数
  • 有阴影函数
  • 有阴影且多次反射函数

这些函数都是离散的，所以需要采样来得到。

无阴影函数

输入：顶点法线 n n n、采样方向 w i w_i wi​
输出： 1 π m a x ( n ⋅ w i ， 0 ) \frac{1}{\pi} max(n\cdot w_i，0) π1​max(n⋅wi​，0)

有阴影函数

输入：顶点位置 v v v，顶点法线 n n n、采样方向 w i w_i wi​
处理： V i s i b i l i t y = 在 v 点向 w i 方向发射射线，检测是否碰到物体 Visibility =在v点向w_i方向发射射线，检测是否碰到物体 Visibility=在v点向wi​方向发射射线，检测是否碰到物体
输出： 1 π m a x ( n ⋅ w i ， 0 ) ∗ V i s i b i l i t y \frac{1}{\pi} max(n\cdot w_i，0) * Visibility π1​max(n⋅wi​，0)∗Visibility

有阴影且多次反射函数

需要先进行有阴影函数处理，得到每个顶点的SH系数。
对于每个顶点，递归调用函数computeInterreflectionSH（&m_TransportSHCoeffs, v, n, scene, 1）。

Func(求解顶点的球谐系数T,顶点位置v,顶点法线n,场景指针,当前弹射次数){
	if (当前弹射次数>最大弹射次数) return 球谐系数为0;
	对每一个顶点在球面采样
	for(theta = 0->pi, phi = 0->2*pi){
		1. 在采样方向与物体求交，得到求交信息（三角形顶点编号，交点位置，重心坐标）;
		2. 插值计算得到相交点球谐函数系数interpolateSH。
		3. 递归调用Func(相交点信息)，得到弹射返回的传输项球谐系数nextBouncesCoeffs。
		4. 将interpolateSH（当前采样方向直接传输项） + nextBouncesCoeffs（当前采样方向多次弹射传输项）
	}
	得到采样方向的总传输项归一化(*coeffs)[i] /= sample_side * sample_side;
	并将这数据return;
}

源码：

    /// <summary>
    /// 递归计算相互反射
    /// </summary>
    /// <param name="directTSHCoeffs">当前顶点传输项球谐系数</param>
    /// <param name="pos">顶点位置</param>
    /// <param name="normal">顶点法线</param>
    /// <param name="scene">场景</param>
    /// <param name="bounces">弹射次数</param>
    /// <returns></returns>
    std::unique_ptr<std::vector<double>> computeInterreflectionSH(Eigen::MatrixXf* directTSHCoeffs, const Point3f& pos, const Normal3f& normal, const Scene* scene, int bounces)
    {
        std::unique_ptr<std::vector<double>> coeffs(new std::vector<double>());
        coeffs->assign(SHCoeffLength, 0.0);

        if (bounces > m_Bounce)
            return coeffs;

        // 弹射次数
        const int sample_side = static_cast<int>(floor(sqrt(m_SampleCount)));
        std::random_device rd;
        std::mt19937 gen(rd());
        std::uniform_real_distribution<> rng(0.0, 1.0);
        for (int t = 0; t < sample_side; t++) {
            for (int p = 0; p < sample_side; p++) {
                double alpha = (t + rng(gen)) / sample_side;
                double beta = (p + rng(gen)) / sample_side;
                double phi = 2.0 * M_PI * beta;
                double theta = acos(2.0 * alpha - 1.0);

                Eigen::Array3d d = sh::ToVector(phi, theta);
                const auto wi = Vector3f(d.x(), d.y(), d.z());
                double H = wi.normalized().dot(normal);
                // 光线与物体求交
                Intersection its;
                if (H > 0.0 && scene->rayIntersect(Ray3f(pos, wi.normalized()), its))
                {
                    MatrixXf normals = its.mesh->getVertexNormals();//顶点法线
                    Point3f idx = its.tri_index; //三角形序号
                    Point3f hitPos = its.p;      //交点位置
                    Vector3f bary = its.bary;    // 重心坐标

                    // 计算得到法线插值
                    Normal3f hitNormal =
                        Normal3f(normals.col(idx.x()).normalized() * bary.x() +
                            normals.col(idx.y()).normalized() * bary.y() +
                            normals.col(idx.z()).normalized() * bary.z())
                        .normalized();

                    // 递归调用
                    auto nextBouncesCoeffs = computeInterreflectionSH(directTSHCoeffs, hitPos, hitNormal, scene, bounces + 1);

                    // 复写SH系数
                    for (int i = 0; i < SHCoeffLength; i++)
                    {
                        //插值得到重心坐标传输项球谐函数
                        auto interpolateSH = (directTSHCoeffs->col(idx.x()).coeffRef(i) * bary.x() +
                            directTSHCoeffs->col(idx.y()).coeffRef(i) * bary.y() +
                            directTSHCoeffs->col(idx.z()).coeffRef(i) * bary.z());

                        // 因为这里假设所有表面都是漫反射，所以每个方向的光照都是相同的。
                        // 因此，间接光照的值： L_间接 = L * T_间接 （L为环境光 * T为传输项）
                        // 因此，该方向的直接光照 = L * T_直接 + L_间接 = L * T_直接 + L * T_间接
                        // (注意：这里 (L_间接) 不用乘以 (1- T_直接) 因为我们做光线追踪时，只有(1- T_直接)范围内才有间接光)
                        // 综上：当前顶点传输项 T = T + T_间接，因此用加号直接相加即可
                        (*coeffs)[i] += (interpolateSH + (*nextBouncesCoeffs)[i]) * H;
                    }
                }
            }
        }

        // 这里不应该简单的除以sample_side * sample_side，
        // 而是应该在采样中乘以立体角，而立体角=4pi/采样数
        // 所以应该乘以4pi/sample_side * sample_side

		// 源码
        //for (unsigned int i = 0; i < coeffs->size(); i++) {
        //    (*coeffs)[i] /= sample_side * sample_side;
        //}
        // 修改代码
        float invSample = 1 / sample_side * sample_side;
        for (unsigned int i = 0; i < coeffs->size(); i++) {
            (*coeffs)[i] = 4.0f * M_PI * invSample;
        }
        return coeffs;
    }

3. 保存计算得到的L和T的球谐系数

保存为txt文档

三、使用预计算数据进行渲染

  • 将预计算好的光照球谐系数作为Uniform参数传入Shader
  • 将预计算好的顶点传输项系数作为顶点数据传入Shader

使用顶点着色方式着色

//prtVertex.glsl
attribute vec3 aVertexPosition;
attribute vec3 aNormalPosition;
attribute mat3 aPrecomputeLT;

uniform mat4 uModelMatrix;
uniform mat4 uViewMatrix;
uniform mat4 uProjectionMatrix;

uniform mat3 uPrecomputeL[3];

varying highp vec3 vColor;

float L_dot_LT(mat3 PrecomputeL, mat3 PrecomputeLT) {
	  vec3 L_0 = PrecomputeL[0];
	  vec3 L_1 = PrecomputeL[1];
	  vec3 L_2 = PrecomputeL[2];
	  vec3 LT_0 = PrecomputeLT[0];
	  vec3 LT_1 = PrecomputeLT[1];
	  vec3 LT_2 = PrecomputeLT[2];
	  return dot(L_0, LT_0) + dot(L_1, LT_1) + dot(L_2, LT_2);
}

void main(void) {
	  for(int i = 0; i < 3; i++)
	  {
	    vColor[i] = L_dot_LT(aPrecomputeLT, uPrecomputeL[i]);
	  }
	  gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix * vec4(aVertexPosition, 1.0);
}

将颜色直接输出（经过色调映射）

//prtFragment.glsl
#ifdef GL_ES
precision mediump float;
#endif
varying highp vec3 vColor;

vec3 toneMapping(vec3 color){
    vec3 result;
      for (int i=0; i<3; ++i) {
        result[i] = pow(color[i], 0.45);
    }

    return result;
}

void main(){
  vec3 color = toneMapping(vColor); 
  gl_FragColor = vec4(color, 1.0);
}

四、基于漫反射材质的PRT总结

可以看出，基于漫反射材质的PRT，本质上就是计算好每个顶点接收四面八方光照的方程，再与光照相乘得到最终结果。
在这里插入图片描述

什么时候会用到快速的场景切换呢？

我们已知，PRT要求预计算的场景不可动，只能切换或旋转球谐光源。所以PRT只能用于静态物体；而在多个球谐光源之间插值或转换，也可以理解为切换球谐光源。

所以可以用在：

  1. 凌晨，早晨，正午，下午，晚上，傍晚几个球谐光源之间转化，来改变场景中动态物体的全局光照。
  2. 如果只对不发生形变的物体，在局部空间下计算传输项，则可以在场景移动，根据周围环境的光照探针计算光照，只是物体不能发生形变，且只能计算自遮挡，无法被环境中其他物体遮挡产生阴影。

与光照烘培的区别

如果不改变环境光照，PRT可被替代为光照烘培，即直接计算每个点在当前环境下的颜色值，并记录在一张纹理上。

因此，基于漫反射的PRT相比于光照烘培，只是多了环境光可旋转，可改变这样一个条件，而付出的代价则是9倍（3阶球谐记录）的存储空间。

那么PRT有什么优势呢？？？？？

五、基于Glossy物体的PRT

每个顶点多记录一维数据（视口俯仰角度），根据摄像机方向和物体法线方向的夹角，得到该夹角下的球谐系数，再计算得到该夹角下的颜色值。

如何得到Glossy物体系数矩阵？？？
之后再补充！！

这相比于烘培就有很大的优势了，可以实时得到光泽反射的效果（区别于镜面反射，即可以反射一定的全局光照，但只是一个很模糊的结果），这是光照烘培做不到的。

但开销同样巨大，一般情况下，光泽反射需要的阶数更高，通常需要16 * 16（4阶）或25 * 25（5阶）倍的显存开销。

六、游戏界环境是否使用PRT来做全局光照

现代实时渲染 一般不使用 PRT来做全局，
一是因为对显存开销巨大
二是因为现代GPU性能相比于预处理年代【2002】已经好了很多倍，不需要如此大量的预处理，很多计算可以放如GPU中实时计算。
三是因为PRT应用了球谐函数做拟合，本身就是一种很大的近似，而现代工业中，如果需要做全局光照的，一般是3A游戏，而PRT的效果显然达不到。

那我们就没必要学习吗？？

不，PRT开创了通过预计算得到实时全局光照的思想。
PRT 技术或许很少用在工业中，但这种思想则被用在各种技术中！预计算得到实时全局光照的思想，之后可能会更多的应用到VR，数字孪生，开放世界中。

另外两类全局光照的开创性代表是：

  • 以RSM为代表的实时计算全局光照（VXGI，DDGI等）
  • 以SSAO为代表的屏幕空间全局光照（HBAO，SSR等）

这两类则更为我们所熟知！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1025866.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++ - 异常介绍和使用

C++ - 异常介绍和使用

前言 我们在日常编写代码的时候&#xff0c;难免会出现编写错误带来程序的奔溃&#xff0c;或者是用户在使用我们编写的程序时候&#xff0c;使用错误所带来程序的奔溃。 在C 当中 可以对你觉得可能发生 错误 的地方在运行之前进行判断&#xff0c;发生错误可以给出提示。 C…
阅读更多...
JOSEF约瑟 智能电流继电器KWJL-20/L KWLD26 零序孔径45mm 柜内导轨式安装

JOSEF约瑟 智能电流继电器KWJL-20/L KWLD26 零序孔径45mm 柜内导轨式安装

KWJL-20智能电流继电器 零序互感器&#xff1a; KWLD80 KWLD45 KWLD26 KWJL-20 一、产品概述 KWJL-20系列智能剩余电流继电器&#xff08;以下简称继电器&#xff09;适用于交流电压至660V或更高的TN、TT、和IT系统&#xff0c;频率为50Hz。通过零序电流互感器检测出超过…
阅读更多...
TS编译器选项compilerOptions指定编译ES版本和模块化使用规范

TS编译器选项compilerOptions指定编译ES版本和模块化使用规范

compilerOptions是TS的编译器选项&#xff0c;主要在tsconfig.json文件中用于对ts编译为js文件时进行配置 "compilerOptions" : { 配置项 } 一、target指定ts被编译的ES版本 {// compilerOptions 编译器选项"compilerOptions": {// target 用来指定ts被编…
阅读更多...
寻找AI-Native创业者

寻找AI-Native创业者

亲爱的科技探险家们和代码魔法师们&#xff1a; 未来的钟声已经敲响&#xff0c;预示着一场极度炫酷的虚拟现实游戏即将展开。从初期简单的智能识别&#xff0c;到设计师级别的图纸设计&#xff0c;生成式AI技术&#xff08;Generative AI&#xff09;以其独特理念和创新模式重…
阅读更多...
基于springboot+vue的在线购房(房屋租赁)系统

基于springboot+vue的在线购房(房屋租赁)系统

博主主页&#xff1a;猫头鹰源码 博主简介&#xff1a;Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容&#xff1a;毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…
阅读更多...
Java21的新特性

Java21的新特性

Java语言特性系列 Java5的新特性Java6的新特性Java7的新特性Java8的新特性Java9的新特性Java10的新特性Java11的新特性Java12的新特性Java13的新特性Java14的新特性Java15的新特性Java16的新特性Java17的新特性Java18的新特性Java19的新特性Java20的新特性Java21的新特性Java22…
阅读更多...
Java下打印直角三角型（另一个方向）

Java下打印直角三角型（另一个方向）

代码如下&#xff1a; public class MyWork {public static void main(String[] args) {int num 5;for (int i 0; i < num; i) {for (int j 0; j < i; j) {System.out.print("-");}for (int j 0; j < num - i; j) {System.out.print("*");}S…
阅读更多...
Ubuntu 安装 CUDA 与 OPENCL

Ubuntu 安装 CUDA 与 OPENCL

前言&#xff1a;最近需要做一些GPU并行计算&#xff0c;因而入坑CUDA和OPENCL&#xff0c;两者都有用到一些&#xff0c;刚好有点时间&#xff0c;同时记录一些学习过程&#xff0c;排掉一些坑&#xff0c;这篇是环境安装篇&#xff0c;基本跟着走就没什么问题&#xff0c;环境…
阅读更多...
字节跳动大规模多云CDN管理与产品化实践

字节跳动大规模多云CDN管理与产品化实践

近日&#xff0c;火山引擎边缘云融合CDN团队负责人孙益星在LiveVideoStack Con 2023上海站围绕融合CDN团队持续建设多云CDN平台的演进过程&#xff0c;结合建设过程中面临的难点和挑战&#xff0c;介绍了融合CDN团队接下来的主要投入方向&#xff0c;分享了火山引擎在多云应用架…
阅读更多...
tp5.1 致命错误: Call to undefined method think\Cache::get()

tp5.1 致命错误: Call to undefined method think\Cache::get()

致命错误: 致命错误: Call to undefined method think\Cache::get() 原因&#xff1a;&#xff08;引用类错误&#xff09; thinkphp5.1中有两个Cache类&#xff1a;think\Cache和think\facade\Cache。 官方文档中说使用think\Cache&#xff0c;但实际是使用think\facade\Cac…
阅读更多...
SQL Server数据库中了360后缀勒索病毒怎么办，勒索病毒解密数据恢复

SQL Server数据库中了360后缀勒索病毒怎么办，勒索病毒解密数据恢复

随着互联网的发展&#xff0c;网络安全问题日益凸显&#xff0c;勒索病毒已经成为当今数字威胁中的一大主要犯罪行为之一。其中&#xff0c;360后缀勒索病毒作为一种常见的数据库攻击形式&#xff0c;对数据库的安全性提出了极大挑战。近期我们收到很多企业的求助&#xff0c;企…
阅读更多...
RocketMQ 源码分析——NameServer

RocketMQ 源码分析——NameServer

文章目录 为什么要学RocketMQ源码RocketMQ源码中的技术亮点RocketMQ 模块结构NameServer 源码分析NameServer 整体流程NameServer 启动流程加载KV配置构建NRS通讯接收路由、心跳信息定时任务剔除超时Broker NameServer设计亮点读写锁存储基于内存NameServer无状态化 为什么要学…
阅读更多...
SpringIOC之Lifecycle 接口

SpringIOC之Lifecycle 接口

博主介绍&#xff1a;✌全网粉丝4W&#xff0c;全栈开发工程师&#xff0c;从事多年软件开发&#xff0c;在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战&#xff0c;博主也曾写过优秀论文&#xff0c;查重率极低&#xff0c;在这方面有丰富的经验…
阅读更多...
计算机等级考试信息安全三级填空题-二

计算机等级考试信息安全三级填空题-二

1.信息安全的五个根本属性是&#xff1a;机密性、完整性可控性、不可否认性和完整性。 2.在Windows系统中&#xff0c;查看当前已经启动的效劳列表的命令是&#xff1a;net start 3.在数据库中&#xff0c;删除表的命令是&#xff1a;DROP 4.在信息资产治理中&#xff0c;标准…
阅读更多...
zabbix的原理与安装

zabbix的原理与安装

一、Zabbix介绍 1、zabbix 是什么&#xff1f; zabbix是一个开源的IT基础监控软件&#xff0c;能实时监控网络服务&#xff0c;服务器和网络设备的状态&#xff0c;如网络使用&#xff0c;CPU负载、磁盘空间等&#xff0c;主要是包括数据的收集、报警和通知的可视化界面zabbi…
阅读更多...
Java下打印1-100以内的质数

Java下打印1-100以内的质数

代码如下&#xff1a; public class MyWork {public static void main(String[] args) {System.out.println("100以内的质数如下&#xff1a;");for (int num 0; num < 100; num) {if (2 num) {System.out.print(num " ");continue;}for (int i 2;…
阅读更多...
晚上弱光拍照不够清晰，学会这几招画面清晰效果好

晚上弱光拍照不够清晰，学会这几招画面清晰效果好

很多小伙伴喜欢夜晚拍摄&#xff0c;然而拍摄出来的照片经常画面偏暗甚至模糊不清&#xff0c;这是怎么回事&#xff1f; 弱光环境是很多人都比较头疼的拍摄场合&#xff0c;由于光线弱曝光不好把控&#xff0c;并且还很容易出现细节性问题&#xff0c;想要将照片拍好就非常不…
阅读更多...
全网最详细的自动化测试（Jenkins 篇）

全网最详细的自动化测试（Jenkins 篇）

学习 Jenkins 自动化测试的系列文章 Robot Framework 概念Robot Framework 安装Pycharm Robot Framework 环境搭建Robot Framework 介绍Jenkins 自动化测试 1. Robot Framework 概念 Robot Framework是一个基于Python的&#xff0c;可扩展的关键字驱动的自动化测试框架。 …
阅读更多...
MongoDB【部署 02】mongodb使用配置文件启动、添加为系统服务及自启动（一个报错：[13436][NotMasterOrSecondary]）

MongoDB【部署 02】mongodb使用配置文件启动、添加为系统服务及自启动（一个报错：[13436][NotMasterOrSecondary]）

MongoDB使用配置文件启动、添加为系统服务及设置自启动 1.是什么2.下载安装启动配置2.1 下载2.2 安装2.3 配置2.4 使用配置文件启动 3.设置系统服务及自启动3.1 设置为系统服务3.2 自启动 1.是什么 【以下内容来自ChatGPT3.5】 MongoDB是一个流行的开源文档型数据库管理系统&a…
阅读更多...
IP地址与代理IP：了解它们的基本概念和用途

IP地址与代理IP：了解它们的基本概念和用途

在互联网世界中&#xff0c;IP地址和代理IP是两个常见但不同的概念&#xff0c;它们在网络通信、隐私保护和安全方面发挥着重要作用。本文将介绍什么是IP地址和代理IP&#xff0c;以及它们在网络中的作用和应用。 IP地址是什么&#xff1f; IP地址&#xff0c;全称为Internet…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023