文章目录
- 前言
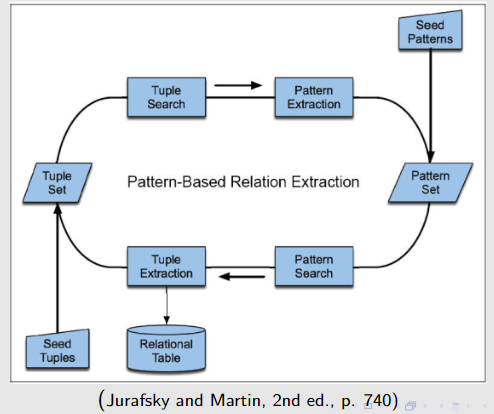
- 一、常见的排序算法
- 二、快速排序的非递归版本
- 三、具体步骤
- 四、非递归的代码实现
- 五、时间复杂度
- 4.1最好情况
- 4.2最坏情况
- 六、总结
前言
手撕排序算法第六篇:快速排序!
从本篇文章开始,我会介绍并分析常见的几种排序,例如像插入排序,冒泡排序,希尔排序,选择排序,快速排序,堆排序,归并排序等等!
这篇文章我先来给大家手撕一下快速排序!
大家可以点下面的链接去阅读其他的排序算法:
C语言手撕排序算法
正文开始!
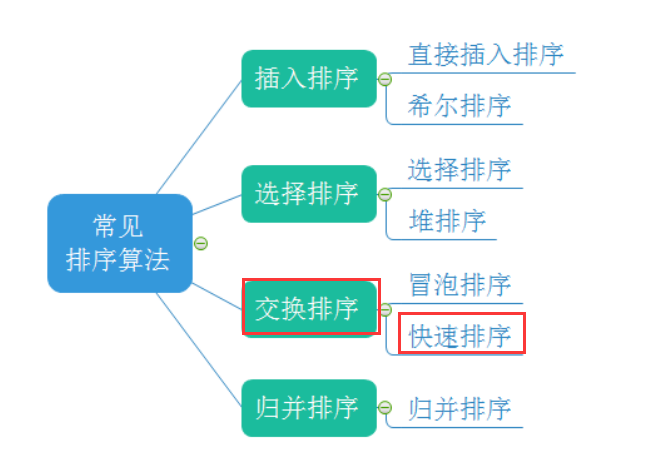
一、常见的排序算法
二、快速排序的非递归版本
上节课我们写了快速排序的递归版本的三种实现,**递归也有不好的地方,递归最大的缺陷是如果排序调用的栈帧太深,可能会导致栈溢出。**因为栈的大小一般只有8M。
快排的非递归是实现其实是利用了栈的特性,因为栈的特点是先进后出。那么非递归版本是如何实现的呢?其实还是利用栈实现了递归的思想。
在上篇文章的递归实现,主要是将大区间划分为多个小区间,然后再对每个小区间进行排序,直到每个小区间都有序并且无法在划分的时候,就完成排序。
非递归的思想和递归差不多,接下来带大家看看非递归版本。
三、具体步骤
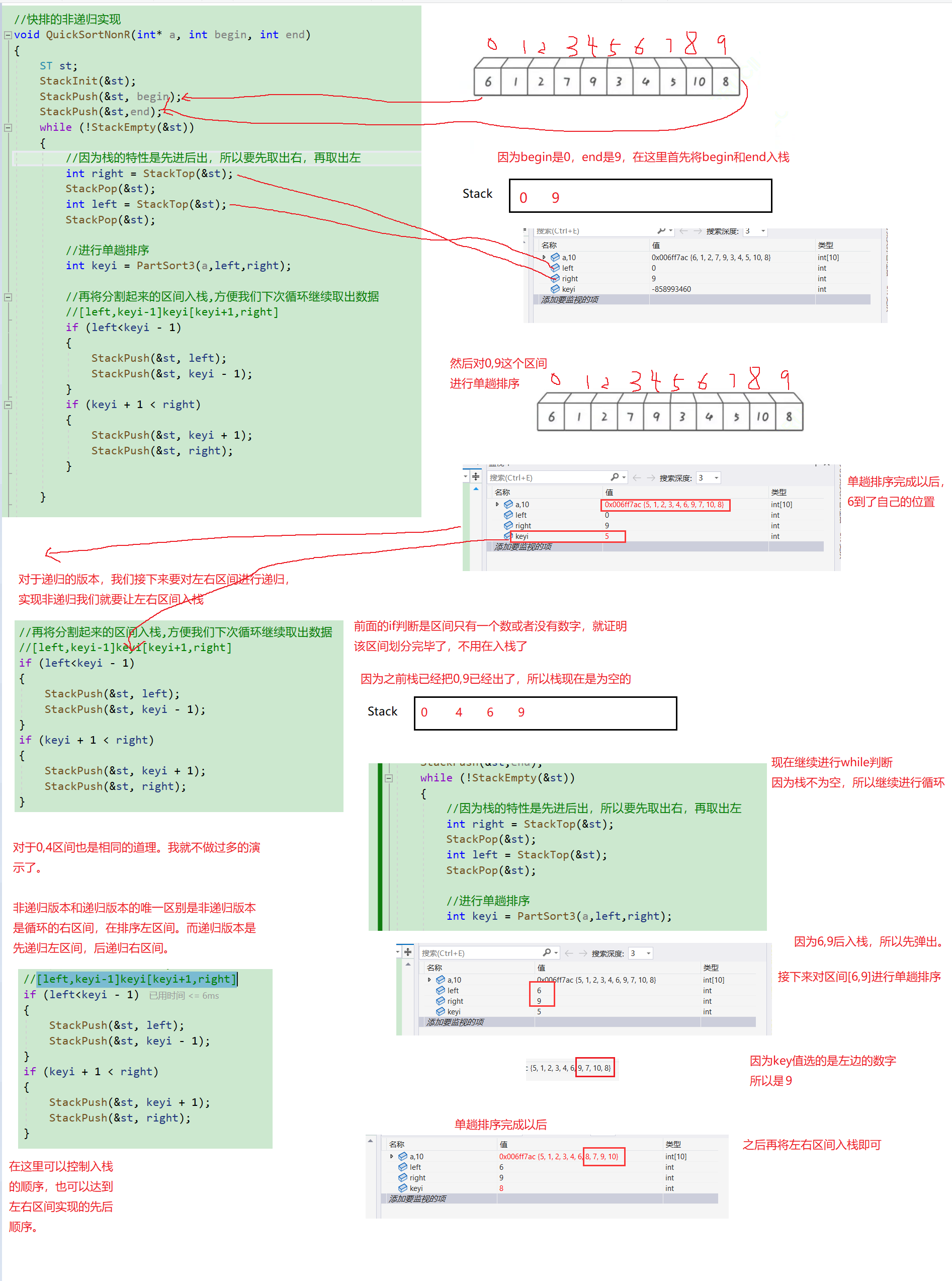
- 我们先将所给的区间进行入栈,然后取出栈顶元素赋给right(先进后出,所以先取出来的是右下标),然后再删除堆顶的元素。再取出栈顶元素赋给left,然后再删除栈顶元素。对取出来的的区间范围进行单趟排序.
- 排序完成返回一个keyi的值,这个值又把数组分成三个区间[0,keyi-1],keyi,[keyi+1,right].
- 我们再对小区间重复1操作,直到小区间无法被划分,证明排序完成。
让我们画图再简单理解一下:
四、非递归的代码实现
//前后指针法
int PartSort3(int* a, int left, int right)
{
//int midi = GetMidIndex(a,left,right);
//Swap(&a[midi],&a[left]);
int key = a[left];
int prev = left;
int cur = prev + 1;
while (cur<=right)
{
if (a[cur] < key&&a[++prev]!=a[cur])//遇到比ket小的值先++prev,接下来防止自己和自己交换
Swap(&a[prev], &a[cur]);
cur++;
}
Swap(&a[left],&a[prev]);
return prev;
}
//快排的非递归实现
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st,end);
while (!StackEmpty(&st))
{
//因为栈的特性是先进后出,所以要先取出右,再取出左
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
//进行单趟排序
int keyi = PartSort3(a,left,right);
//再将分割起来的区间入栈,方便我们下次循环继续取出数据
//[left,keyi-1]keyi[keyi+1,right]
if (left<keyi - 1)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
if (keyi + 1 < right)
{
StackPush(&st, keyi + 1);
StackPush(&st, right);
}
}
StackDestory(&st);
}
void TestQuickSort()
{
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
printf("排序前:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
QuickSortNonR(a, 0,sizeof(a) / sizeof(a[0])-1);
printf("排序后:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
TestQuickSort();
return 0;
}
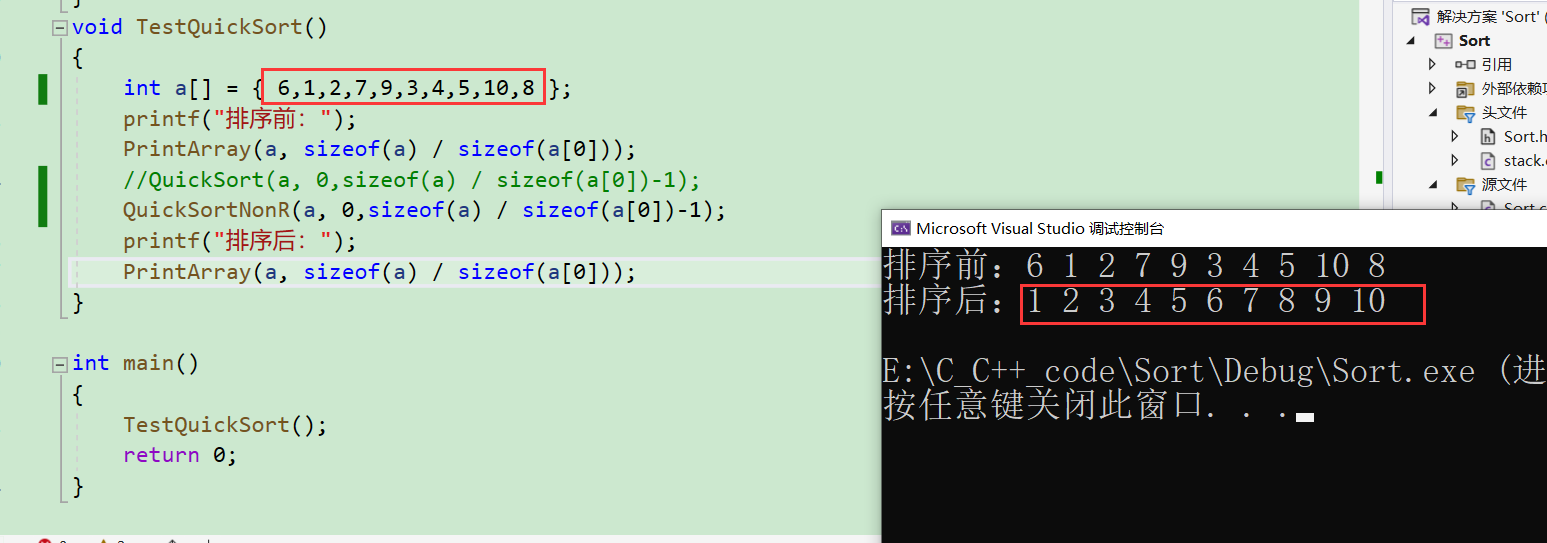
在这里我们发现要实现快速排序的非递归版本,首先要先实现一个栈结构!
在这里给出栈的代码,大家可以直接去使用。
五、时间复杂度
非递归时间复杂度依旧和递归一样,具体分析情况请参考上篇[ 数据结构 – 手撕排序算法第六篇 ] 快速排序
4.1最好情况
O(N*logN)
4.2最坏情况
O(N^2)
六、总结
对于快速排序我们到这里递归版本和非递归版本的实现就结束了。对于快速排序的递归的三个版本还是要加强理解,还有后面的优化部分,小区间使用直接插入排序完成和三数取中的优化,需要着重理解一下。
(本章完!)



![[附源码]计算机毕业设计Python高校商铺管理系统论文(程序+源码+LW文档)](https://img-blog.csdnimg.cn/1775b28cef8f4e96801aa314c9f592c7.png)