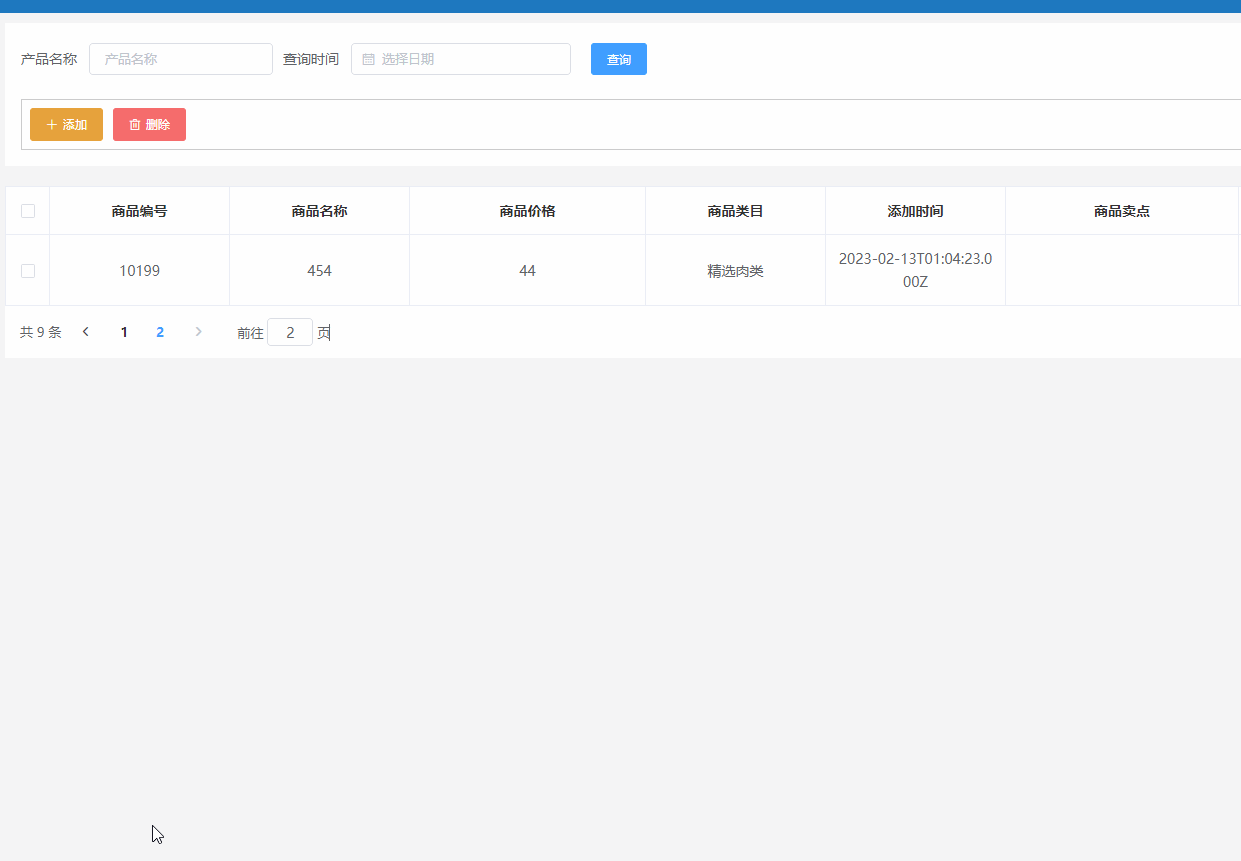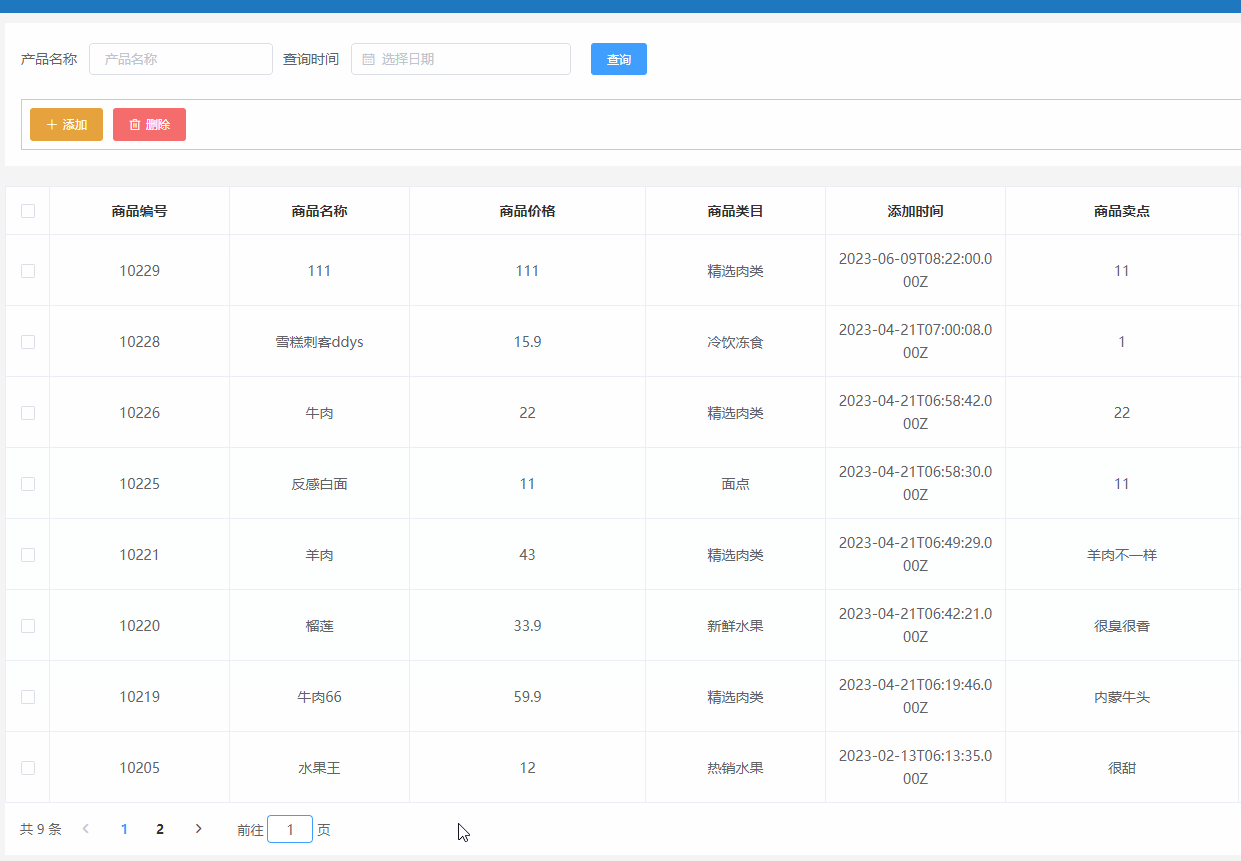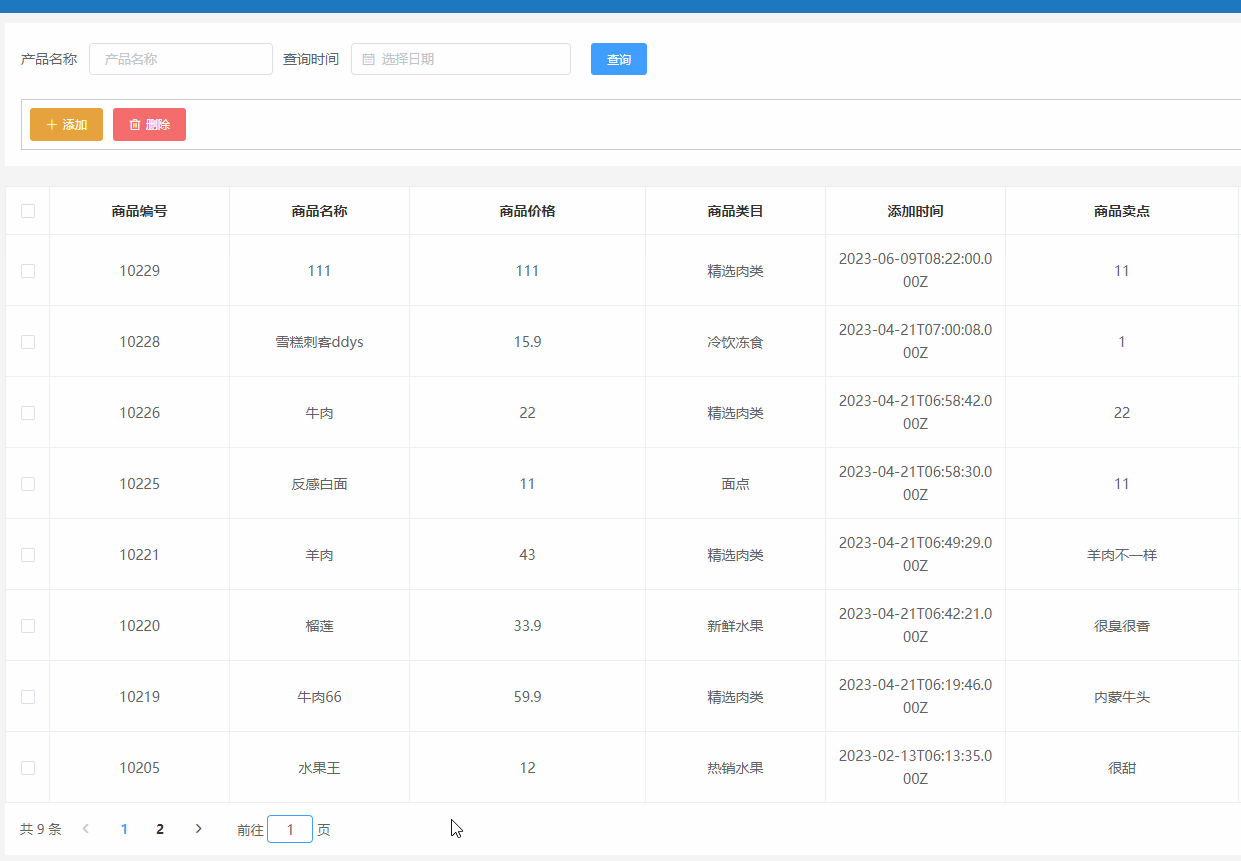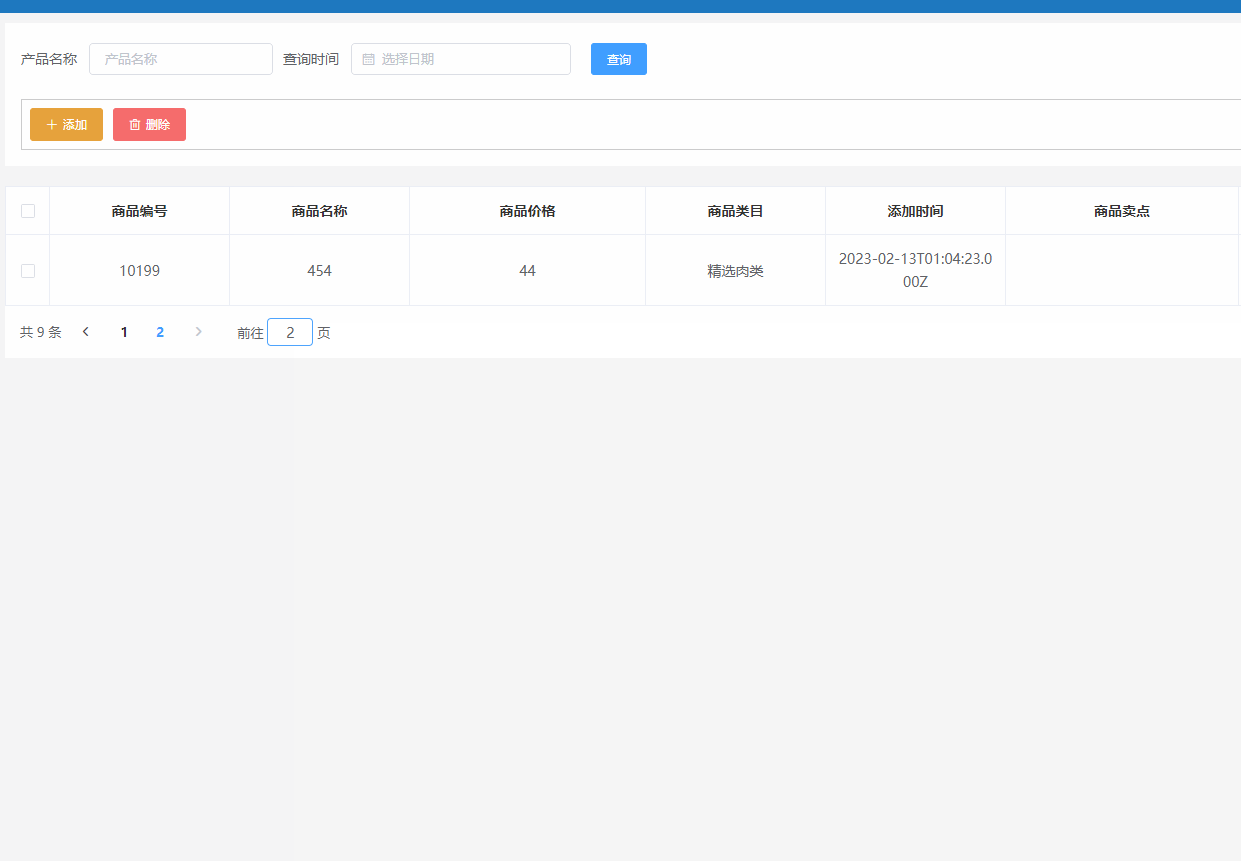
传播
由于块与块之间具有参考关系,提升被参考块的质量,可以改善后续参考块的质量

Pn+1帧中CU0,1完全参考Pn的CU1,1。且Pn+1帧中CU0,1块帧内预测和帧间预测的代价分别为 c x , y n + 1 ( 0 , 0 ) c_{x,y}^{n+1}(0,0) cx,yn+1(0,0)和 c x , y n + 1 ( d 0 , d 1 ) c_{x,y}^{n+1}(d0,d1) cx,yn+1(d0,d1),其中x,y表示这里CU的坐标,也就是(x,y)=(0,1),为了一般性,所以用x,y表示。
如果 c x , y n + 1 ( 0 , 0 ) c_{x,y}^{n+1}(0,0) cx,yn+1(0,0)和 c x , y n + 1 ( d 0 , d 1 ) c_{x,y}^{n+1}(d0,d1) cx,yn+1(d0,d1)相差不大,说明Pn+1帧中CU0,1块从Pn的CU1,1获取的信息很少;如果 c x , y n + 1 ( 0 , 1 ) c_{x,y}^{n+1}(0,1) cx,yn+1(0,1)比 c x , y n + 1 ( d 0 , d 1 ) c_{x,y}^{n+1}(d0,d1) cx,yn+1(d0,d1)小很多说明Pn+1帧中CU0,1块的大部分信息都可以从Pn的CU1,1块获得,极端情况,如果 c d 0 , d 1 n + 1 c_{d0,d1}^{n+1} cd0,d1n+1为0,说明说明Pn+1帧中CU0,1块的全部信息都可以从Pn的CU1,1块获得。因此可以简单地用 p c x , y n + 1 = c x , y n + 1 ( 0 , 0 ) − c x , y n + 1 ( d 0 , d 1 ) pc_{x,y}^{n+1}=c_{x,y}^{n+1}(0,0)-c_{x,y}^{n+1}(d0,d1) pcx,yn+1=cx,yn+1(0,0)−cx,yn+1(d0,d1)表示Pn+1帧中CU0,1块从Pn的CU1,1继承的信息。
由于Pn+1帧中CUx,y块编码参数选择不同,会导致 p c x , y n + 1 = c x , y n + 1 ( 0 , 0 ) − c x , y n + 1 ( d 0 , d 1 ) pc_{x,y}^{n+1}=c_{x,y}^{n+1}(0,0)-c_{x,y}^{n+1}(d0,d1) pcx,yn+1=cx,yn+1(0,0)−cx,yn+1(d0,d1)的使用率不同,因此 p f x , y n + 1 = c x , y n + 1 ( 0 , 0 ) − c x , y n + 1 ( d 0 , d 1 ) c x , y n + 1 ( 0 , 0 ) pf_{x,y}^{n+1}=\frac{c_{x,y}^{n+1}(0,0)-c_{x,y}^{n+1}(d0,d1)}{c_{x,y}^{n+1}(0,0)} pfx,yn+1=cx,yn+1(0,0)cx,yn+1(0,0)−cx,yn+1(d0,d1)表示Pn+1帧中CU0,1块反向传播给Pn的CU1,1块的传播率,或者说是Pn+1帧对Pn帧中CU1,1块的继承信息的利用率,也就是Pn+1帧CUx,y选择不同参数时,对 p c x , y n + 1 = c x , y n + 1 ( 0 , 0 ) − c x , y n + 1 ( d 0 , d 1 ) pc_{x,y}^{n+1}=c_{x,y}^{n+1}(0,0)-c_{x,y}^{n+1}(d0,d1) pcx,yn+1=cx,yn+1(0,0)−cx,yn+1(d0,d1)的使用率。
Pn+1帧中CU0,1块的传播给Pn的CU1,1块的总信息 p a x , y n + 1 = p c x , y n + 1 + p f x , y n + 1 ⋅ p i x , y n + 1 pa_{x,y}^{n+1}=pc_{x,y}^{n+1}+pf_{x,y}^{n+1} \cdot pi_{x,y}^{n+1} pax,yn+1=pcx,yn+1+pfx,yn+1⋅pix,yn+1所有参考Pn帧CU1,1块的CU块,反向传播给它的信息量为 p i x , y n = p a x 1 , y 1 n 1 ⋅ w 1 + p a x 2 , y 2 n 2 ⋅ w 2 + p a x 3 , y 3 n 3 ⋅ w 3 + . . . pi_{x,y}^{n}=pa_{x1,y1}^{n1} \cdot w1 + pa_{x2,y2}^{n2} \cdot w2 + pa_{x3,y3}^{n3} \cdot w3 + ... pix,yn=pax1,y1n1⋅w1+pax2,y2n2⋅w2+pax3,y3n3⋅w3+...,其中w表示权重,也就是区域的重叠面积,针对上图中 p i 1 , 1 n = p a 1 , 0 n + 1 ⋅ 1 + p a 1 , 1 n + 1 ⋅ 1 pi_{1,1}^{n}=pa_{1,0}^{n+1} \cdot 1 + pa_{1,1}^{n+1} \cdot 1 pi1,1n=pa1,0n+1⋅1+pa1,1n+1⋅1
在x265中使用estimateCUPropagate函数计算 p a x , y n pa_{x,y}^{n} pax,yn:
p a x , y n = p c x , y n + p f x , y n ⋅ p i x , y n = ( c x , y n ( 0 , 0 ) + p i x , y n ) ⋅ c x , y n ( 0 , 0 ) − c x , y n ( d 0 , d 1 ) c x , y n ( 0 , 0 ) = ( c x , y n ( 0 , 0 ) + p i x , y n ) ⋅ p f x , y n \begin{align} pa_{x,y}^{n}&=pc_{x,y}^{n}+pf_{x,y}^{n} \cdot pi_{x,y}^{n} \\ &=(c_{x,y}^{n}(0,0) + pi_{x,y}^{n}) \cdot \frac{c_{x,y}^{n}(0,0)-c_{x,y}^{n}(d0,d1)}{c_{x,y}^{n}(0,0)} \\ &= (c_{x,y}^{n}(0,0) + pi_{x,y}^{n}) \cdot pf_{x,y}^{n} \end{align} pax,yn=pcx,yn+pfx,yn⋅pix,yn=(cx,yn(0,0)+pix,yn)⋅cx,yn(0,0)cx,yn(0,0)−cx,yn(d0,d1)=(cx,yn(0,0)+pix,yn)⋅pfx,yn
-
上述考虑了只有cutree时,信息量的传播,还需要做两个细微的修正:AQ将各个MB都进行了微调,那么那些被调整的更清晰的MB(QP减小)和变得更模糊的MB(QP变大)也需要进行修正 i n v q s c a l e = 1 a q o f f s e t s t e p inv_qscale=\frac{1}{aq_offset_step} invqscale=aqoffsetstep1
-
在可变帧率条件下,需要根据播放时长进行修正, f p s f a c t o r = 当前帧播放时长 平均一帧播放时长 fps_factor=\frac{当前帧播放时长}{平均一帧播放时长} fpsfactor=平均一帧播放时长当前帧播放时长
-
如下图,中间的B帧同时从前向的P0帧和后向的P1帧都继承了信息,需要按照距离修正传播的cost大小, d i s t a n c e r a t i o = b − p 0 p 1 − p 0 distance_ratio=\frac{b-p0}{p1-p0} distanceratio=p1−p0b−p0
经过以上三个修正,最终结果如下:

p a x , y n = ( p c x , y n ⋅ i n v _ q s c a l e ⋅ f p s _ f a c t o r + p f x , y n ⋅ p i x , y n ) ⋅ d i s t a n c e _ r a t i o = ( c x , y n ( 0 , 0 ) ⋅ i n v _ q s c a l e ⋅ f p s _ f a c t o r + p i x , y n ) ⋅ p f x , y n ⋅ d i s t a n c e r a t i o \begin{align} pa_{x,y}^{n}&=(pc_{x,y}^{n}\cdot inv\_qscale\cdot fps\_factor+pf_{x,y}^{n} \cdot pi_{x,y}^{n})\cdot distance\_ratio \\ &= (c_{x,y}^{n}(0,0) \cdot inv\_qscale \cdot fps\_factor+ pi_{x,y}^{n}) \cdot pf_{x,y}^{n} \cdot distance_ratio \end{align} pax,yn=(pcx,yn⋅inv_qscale⋅fps_factor+pfx,yn⋅pix,yn)⋅distance_ratio=(cx,yn(0,0)⋅inv_qscale⋅fps_factor+pix,yn)⋅pfx,yn⋅distanceratio
以上计算得到的 p a x , y n pa_{x,y}^{n} pax,yn需要根据mv传递到第Pn-1帧,作为对应块的pi值,根据重叠区域面积将其分配到各个块,如上图会根据s1,s2,s3和s4所占面积的比例将 p a 1 , 1 n pa_{1,1}^{n} pa1,1n分配到CU00,CU01,CU10和CU11;同时 p a 2 , 1 n pa_{2,1}^{n} pa2,1n分配到CU10,CU11,CU20和CU21;其中 p a 1 , 1 n pa_{1,1}^{n} pa1,1n和 p a 2 , 1 n pa_{2,1}^{n} pa2,1n都会分配一部分到CU10和CU11,只需要将其叠加即可。
计算 Δ \Delta Δ QP
首先将信息分为两类:第一是继承信息,也就是当前块从参考帧获得的信息,参考帧已经编码完成的情况下,通过同一个参考帧和同一个MV获得的参考块也就固定了,得到的信息也就固定了,并不会因为当前块选择不同的编码参数而发生改变;第二是自身产生的信息,从参考块获取了信息之后,当前块会用不同的编码参数,比如QP,merge,skip,AMVP等模式,编码参数不同时,自身产生的信息也就不同。
继续考虑Pn的CU1,1块,当改变当前块的QP时(也就是增加一个 delta QP), c x , y n + 1 ( 0 , 0 ) c_{x,y}^{n+1}(0,0) cx,yn+1(0,0)和 c x , y n + 1 ( d 0 , d 1 ) c_{x,y}^{n+1}(d0,d1) cx,yn+1(d0,d1)和 p i x , y n pi_{x,y}{n} pix,yn都会发生变化,因为他们都包含了自身产生的信息。但是 c x , y n + 1 ( 0 , 0 ) − c_{x,y}^{n+1}(0,0)- cx,yn+1(0,0)−c_{x,y}^{n+1}(d0,d1)$不会发生变化,因为他是继承的信息。可以这么来考虑,QP的改变导致残差量化结果发生变化,影响的是当前块预测后的结果,在计算失真的时候还有一个参考块,该参考块是通过MV在参考帧获得的,这个时候参考块已经编码完成,并不会因为当前块QP的改变而发生变化。
当前块的QP发生变化时,后续参考该块的CU都会发生变化,也就是 p i x , y n pi_{x,y}^{n} pix,yn也会因为delta QP而产生影响,但是只有新产生的那部分信息 c x , y n ( d 0 , d 1 ) c x , y n ( 0 , 0 ) \frac{c_{x,y}^{n}(d0,d1)}{c_{x,y}^{n}(0,0)} cx,yn(0,0)cx,yn(d0,d1)受影响, ( 1 − c x , y n ( d 0 , d 1 ) c x , y n ( 0 , 0 ) ) ⋅ p i x , y n (1-\frac{c_{x,y}^{n}(d0,d1)}{c_{x,y}^{n}(0,0)}) \cdot pi_{x,y}^{n} (1−cx,yn(0,0)cx,yn(d0,d1))⋅pix,yn是由继承的那部分信息,传递给后续块的,不受delta QP影响。
- 参考块因为delta QP受影响的信息量有 c Δ = c x , y n ( d 0 , d 1 ) + c x , y n ( d 0 , d 1 ) c x , y n ( 0 , 0 ) ⋅ p i x , y n c_{\Delta}=c_{x,y}^{n}(d0,d1)+\frac{c_{x,y}^{n}(d0,d1)}{c_{x,y}^{n}(0,0)} \cdot pi_{x,y}^{n} cΔ=cx,yn(d0,d1)+cx,yn(0,0)cx,yn(d0,d1)⋅pix,yn
- 非参考块因为delta QP受影响的信息量有 c x , y n ( d 0 , d 1 ) c_{x,y}^{n}(d0,d1) cx,yn(d0,d1), 因为非参考块,不被参考,所以后项为0,只有inter cost部份
r Δ = c Δ c x , y n ( d 0 , d 1 ) = 1 + p i x , y n c x , y n ( 0 , 0 ) λ = − d D d R = − d D / d Q P d R / d Q P = α Q s t e p 2 λ ‾ = − r Δ ⋅ d D d R = α ⋅ r Δ Q s t e p ‾ 2 λ = λ ‾ Q s t e p ‾ 2 Q s t e p 2 = 1 r Δ Q s t e p 2 = b 2 ⋅ 2 Q P − 12 3 Q P = 12 + 3 l o g 2 Q s t e p 2 b 2 Q P ‾ = 12 + 3 l o g 2 Q s t e p ‾ 2 b 2 Δ Q P = Q P ‾ − Q P = 3 l o g 2 Q s t e p ‾ 2 b 2 − 3 l o g 2 Q s t e p 2 b 2 = 3 l o g 2 Q s t e p ‾ 2 Q s t e p 2 = 3 l o g 2 1 r Δ = − 3 l o g 2 r Δ \begin{align} & r_{\Delta} = \frac{c_{\Delta}}{c_{x,y}^{n}(d0,d1)}=1+\frac{pi_{x,y}^{n}}{c_{x,y}^{n}(0,0)} \\ & \lambda = -\frac{dD}{dR}=-\frac{dD/dQP}{dR/dQP}=\alpha Qstep^2 \\ & \overline{\lambda} = -\frac{r_{\Delta} \cdot dD}{dR}=\alpha \cdot r_{\Delta} \overline{Qstep}^2 \\ & \lambda = \overline{\lambda} \\ & \frac{\overline{Qstep}^2}{Qstep^2} = \frac{1}{r_{\Delta}} \\ & Qstep^2=b^2 \cdot 2^{\frac{QP-12}{3}} \\ & QP=12 + 3log_{2}^{\frac{Qstep^2}{b^2}} \\ & \overline{QP} = 12 + 3log_{2}^{\frac{\overline{Qstep}^2}{b^2}} \\ & \Delta QP = \overline{QP} - QP = 3log_{2}^{\frac{\overline{Qstep}^2}{b^2}}-3log_{2}^{\frac{Qstep^2}{b^2}} \\ & =3log_{2}^{\frac{\overline{Qstep}^2}{Qstep^2}} \\ & =3log_{2}^{\frac{1}{r_{\Delta}}} = -3log_{2}^{r_{\Delta}} \end{align} rΔ=cx,yn(d0,d1)cΔ=1+cx,yn(0,0)pix,ynλ=−dRdD=−dR/dQPdD/dQP=αQstep2λ=−dRrΔ⋅dD=α⋅rΔQstep2λ=λQstep2Qstep2=rΔ1Qstep2=b2⋅23QP−12QP=12+3log2b2Qstep2QP=12+3log2b2Qstep2ΔQP=QP−QP=3log2b2Qstep2−3log2b2Qstep2=3log2Qstep2Qstep2=3log2rΔ1=−3log2rΔ