目录
蓝桥杯2023年第十四届省赛真题-像素放置
题目描述
输入格式
输出格式
样例输入
样例输出
提示
【思路解析】
【代码实现】
大家觉得写得可以的话,可以加入QQ群907575059.
蓝桥杯2023年第十四届省赛真题-像素放置
时间限制: 3s 内存限制: 320MB 提交: 72 解决: 30
题目描述
小蓝最近迷上了一款名为《像素放置》的游戏,游戏在一个 n × m 的网格棋盘上进行,棋盘含有 n 行,每行包含 m 个方格。玩家的任务就是需要对这n × m 个方格进行像素填充,填充颜色只有黑色或白色两种。有些方格中会出现一个整数数字 x(0 ≤ x ≤ 9),这表示当前方格加上周围八个方向上相邻的方格(分别是上方、下方、左方、右方、左上方、右上方、左下方、右下方)共九个方格内有且仅有 x 个方格需要用黑色填充。
玩家需要在满足所有数字约束下对网格进行像素填充,请你帮助小蓝来完成。题目保证所有数据都有解并且解是唯一的。
输入格式
输入的第一行包含两个整数 n, m,用一个空格分隔,表示棋盘大小。
接下来 n 行,每行包含 m 个字符,表示棋盘布局。字符可能是数字 0 ∼ 9,这表示网格上的数字;字符还有可能是下划线(ASCII 码为 95 ),表示一个不带有数字的普通网格。
输出格式
输出 n 行,每行包含 m 个字符,表示答案。如果网格填充白色则用字符 0
表示,如果网格填充黑色则用字符 1 表示。
样例输入
复制
6 8 _1__5_1_ 1_4__42_ 3__6__5_ ___56___ _688___4 _____6__
样例输出
复制
00011000 00111100 01000010 11111111 01011110 01111110
提示
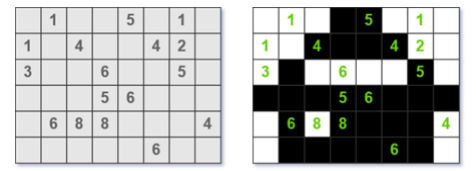
上图左是样例数据对应的棋盘布局,上图右是此局游戏的解。例如第 3 行第 1 列处的方格中有一个数字 3 ,它周围有且仅有 3 个格子被黑色填充,分别是第 3 行第 2 列、第 4 行第 1 列和第 4 行第 2 列的方格。
对于 50% 的评测用例,1 ≤ n, m ≤ 5 ;
对于所有评测用例,1 ≤ n, m ≤ 10 。
【思路解析】
这道题因为n m都不大且只有唯一的答案,可以进行搜索的策略对大量可能性进行舍弃。
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | |||||||
| 1 | |||||||||
对像素表进行搜索时,从左至右,从上至下,则对于任一位置i,j(标红的位置)。它上方标蓝的位置一定不会被以后的决策所影响,我们可以直接开始判断这些蓝色的位置满不满足题目的数字规则,不满足可以舍弃后面的大量可能性,缩短搜索的时间。直到填完时,再判断总的表满不满足数字规则,满足就直接放弃后面的搜索,因为答案是唯一的。
【代码实现】
package LQB;
import java.util.Scanner;
/**
* @ProjectName: study3
* @FileName: Ex8
* @author:HWJ
* @Data: 2023/9/18 23:40
*/
public class Ex8 {
static int[][] ans;
static int[][] map;
static int n;
static int m;
static int[][] uses;
static boolean flag = false;
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
n = input.nextInt();
m = input.nextInt();
map = new int[n][m];
ans = new int[n][m];
uses = new int[n][m];
for (int i = 0; i < n; i++) {
String str = input.next();
char[] chars = str.toCharArray();
for (int j = 0; j < m; j++) {
map[i][j] = chars[j] == '_' ? Integer.MAX_VALUE : (chars[j] - '0');
}
}
dfs(0,0);
}
public static void add(int i, int j) { // 统计当前数组的数字,为方便判断
uses[i][j]++;
if (j + 1 < m) {
uses[i][j + 1]++;
}
if (j - 1 >= 0) {
uses[i][j - 1]++;
}
if (i - 1 >= 0) {
uses[i - 1][j]++;
if (j - 1 >= 0) {
uses[i - 1][j - 1]++;
}
if (j + 1 < m) {
uses[i - 1][j + 1]++;
}
}
if (i + 1 < n) {
uses[i + 1][j]++;
if (j - 1 >= 0) {
uses[i + 1][j - 1]++;
}
if (j + 1 < m) {
uses[i + 1][j + 1]++;
}
}
}
public static void del(int i, int j) { // 如果数组在i,j位置不能放1,就改为0,并删除他的信息
uses[i][j]--;
if (j + 1 < m) {
uses[i][j + 1]--;
}
if (j - 1 >= 0) {
uses[i][j - 1]--;
}
if (i - 1 >= 0) {
uses[i - 1][j]--;
if (j - 1 >= 0) {
uses[i - 1][j - 1]--;
}
if (j + 1 < m) {
uses[i - 1][j + 1]--;
}
}
if (i + 1 < n) {
uses[i + 1][j]--;
if (j - 1 >= 0) {
uses[i + 1][j - 1]--;
}
if (j + 1 < m) {
uses[i + 1][j + 1]--;
}
}
}
static boolean check(int x, int y) { // 检查当前的数组是否满足要求
// 检查的地方已经不可能被以后的策略影响
for (int i = 0; i <= x - 2; i++) {
for (int j = 0; j < m; j++) {
if (map[i][j] == Integer.MAX_VALUE) continue;
if (uses[i][j] != map[i][j]) {
return false;
}
}
}
if (x >= 1)
for (int j = 0; j <= y - 2; j++) {
if (map[x - 1][j] == Integer.MAX_VALUE) continue;
if (uses[x - 1][j] != map[x - 1][j]) return false;
}
return true;
}
// 当做完整个数组的决策后,对数组的所有地方进行检查
static boolean check2() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (map[i][j] == Integer.MAX_VALUE) continue;
if (uses[i][j] != map[i][j]) {
return false;
}
}
}
return true;
}
// i,j 表示现在遍历到那个位置了。
public static void dfs(int i, int j) {
if (flag) {
return;
}
if (i == n) {
if (!check2()) return;
for (int x = 0; x < n; x++) {
for (int y = 0; y < m; y++) {
System.out.print(ans[x][y]);
}
System.out.println();
}
flag = true; // 因为答案是唯一的,所以只要找到一个答案,就立刻退出搜索
return;
}
if (!check(i, j)) return; // 检查当前的棋盘是否满足部分要求
// 对每一种可能性进行搜索。
if (j == m - 1) {
ans[i][j] = 1;
add(i,j);
dfs(i + 1, 0);
ans[i][j] = 0;
del(i,j);
dfs(i + 1, 0);
return;
}
ans[i][j] = 1;
add(i,j);
dfs(i, j + 1);
ans[i][j] = 0;
del(i,j);
dfs(i, j+ 1);
return;
}
}