目录
一、选择题
二、算法题
1、两种排序方法
2、求最小公倍数
一、选择题
1、
解析：
指针和引用是C++中两种不同的变量类型，它们都可以用来访问或修改其他变量的值，但是它们有以下几个区别：
- 引用必须在定义时初始化，而指针可以在任何时候初始化。例如，
int &r = a;是合法的，但是int &r;是不合法的。而int *p;和int *p = &a;都是合法的。 - 引用一旦初始化后不能改变指向的对象，而指针可以改变指向的对象。例如，如果定义了
int &r = a;，那么之后不能再写r = b;来让r指向b，而只能修改r的值。而如果定义了int *p = &a;，那么之后可以写p = &b;来让p指向b。 - 不存在空引用，而存在空指针。引用必须指向一个有效的对象，不能写
int &r = NULL;。而指针可以指向NULL，表示没有指向任何对象。 - 引用不需要解引用操作符，而指针需要。引用可以直接使用，就像它是原变量的别名一样。而指针需要用*号来解引用，才能访问或修改所指对象的值。
- sizeof运算符对引用和指针的结果不同。sizeof运算符返回一个对象或类型所占的字节数。对于引用，它返回的是被引用对象的类型的大小。对于指针，它返回的是指针类型的大小。例如，在64位机器上，如果有
int a = 996; int *p = &a; int &r = a;，那么sizeof(p)返回8，而sizeof(r)返回4。
答案为E。
2、
解析：
拷贝构造函数是一种特殊的构造函数，它在创建对象时，是使用同一类中之前创建的对象来初始化新创建的对象。拷贝构造函数通常用于：
- 通过使用另一个同类型的对象来初始化新创建的对象。例如，
Complex c2(c1);或者Complex c2 = c1;都会调用拷贝构造函数，用c1来初始化c2。 - 复制对象把它作为参数传递给函数。例如，
void Func(Complex c)中，形参c是用拷贝构造函数初始化的，实参是调用函数时传入的对象。 - 复制对象，并从函数返回这个对象。例如，
Complex Func()中，如果函数体内有return c;这样的语句，那么返回值是用拷贝构造函数初始化的，实参是c。
答案为B。
3、
解析：
- 在函数f中，参数u是按值传递的，所以在调用f时，会用实参x或f(x)来初始化u，这会调用一次拷贝构造函数。
- 在函数f中，局部变量v是用u来初始化的，这也会调用一次拷贝构造函数。
- 在函数f中，局部变量w是用v来初始化的，这又会调用一次拷贝构造函数。
- 在函数f中，返回值w是按值返回的，所以在返回时，会用w来初始化一个临时对象，这还会调用一次拷贝构造函数。
- 最后y由临时对象拷贝构造。
但是第二次参数u的拷贝和最后一次拷贝被优化了，所以答案为7。
4、
解析：这个问题的答案是D，重载错误。因为友元函数重载运算符时，必须有至少一个参数，否则无法确定运算符作用于哪个对象。友元函数重载运算符时，因为没有this指针指向对象，因此参数个数保持和原来一样，运算符至少有一个参数，成员函数重载时，因为有this指针的原因，所以参数个数要少一个。
二、算法题
1、两种排序方法
解析：思路很简单，将接受的字符串都放到vector容器中，利用string的operator>=运算符重载来按ascii比较字符串，利用string的size来比较字符串的长度
#include <iostream>
#include<vector>
#include<string>
using namespace std;
int main() {
int n;
cin >> n;
vector<string> vs;
vs.resize(n);
for (auto& str : vs) {
cin >> str;
}
bool lex = true;
bool len = true;
for (int i = 1; i < n; i++) {
if (vs[i - 1] >= vs[i]) { //违反字典序列
lex = false;
break;
}
}
for (int i = 1; i < n; i++) {
if (vs[i - 1].size() >= vs[i].size()) {
len = false;
break;
}
}
if (len && lex)
cout << "both" << endl;
else if (!len && lex)
cout << "lexicographically" << endl;
else if (len && !lex)
cout << "lengths" << endl;
else
cout << "none" << endl;
return 0;
}
// 64 位输出请用 printf("%lld")2、求最小公倍数
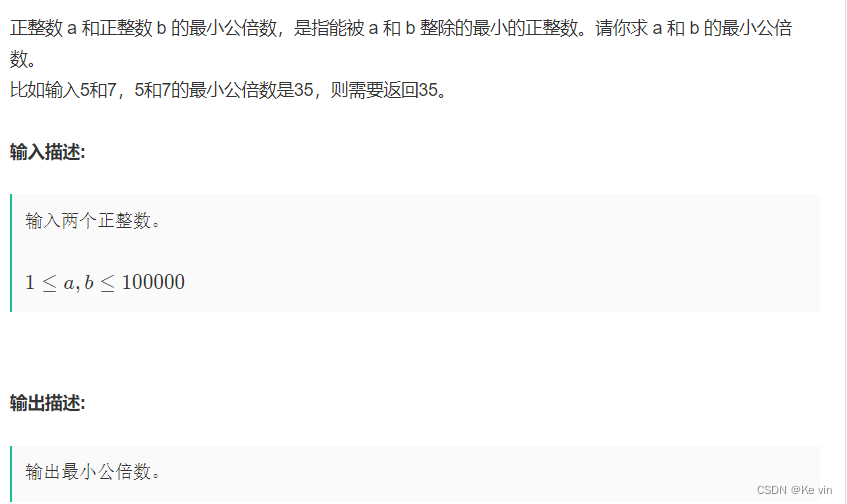解析：最小公倍数 = 两数之积除以最大公约数，这里使用碾转相除法进行最大公约数的求解：即a与b的最大公约数可以转化为a、b之间的余数为两者之间最小的数之间的公约数。所以对于输入的两个数进行连续求余，直到余数为0，求余的分母即为结果。
#include<iostream>
using namespace std;
int gcd(int a, int b) {
int r;
while (r = a % b) {
a = b;
b = r;
}
return b;
}
int main() {
long a, b;
while (cin >> a >> b) {
cout << a* b / gcd(a, b) << endl;
}
return 0;
}
