文章目录
- 1.前言
- 2.消息传递机制
- 1.RecGNN
- 2.ConvGNNs
- 3.GAT
1.前言
相比较于神经网络最基本的网络结构全连接层(MLP),特征矩阵乘以权重矩阵,图神经网络多了一个邻接矩阵。计算形式很简单,三个矩阵相乘再加上一个非线性变换。
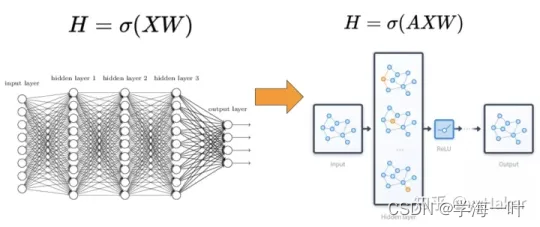
因此一个比较常见的图神经网络的应用模式如下图,输入是一个图,经过多层图卷积等各种操作以及激活函数,最终得到各个节点的表示,以便于进行节点分类、链接预测、图与子图的生成等等任务。
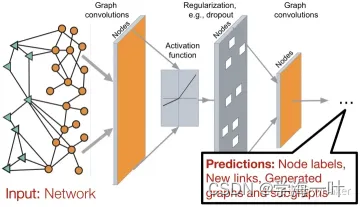
消息传递机制(属性向量优化的方法叫做消息传递机制)是目前GNN的主流研究方向,以下面这个无向图举例说明各类别网络的消息传递机制的不同
2.消息传递机制
1.RecGNN
[
h
1
′
h
2
′
h
3
′
h
4
′
h
5
′
]
=
[
0
1
1
0
1
1
0
0
1
0
1
0
0
1
0
0
1
1
0
0
1
0
0
0
0
]
∗
[
h
1
h
2
h
3
h
4
h
5
]
\begin{bmatrix} h_1^{'}\\h_2^{'}\\h_3^{'}\\h_4^{'}\\h_5^{'} \end{bmatrix} = \begin{bmatrix} 0&1&1&0&1\\1&0&0&1&0\\1&0&0&1&0\\0&1&1&0&0\\1&0&0&0&0 \end{bmatrix} * \begin{bmatrix} h_1\\h_2\\h_3\\h_4\\h_5 \end{bmatrix}
h1′h2′h3′h4′h5′
=
0110110010100100110010000
∗
h1h2h3h4h5
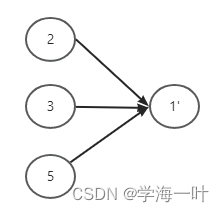
最原始的GNN是SUM求和传递机制, 可以看出
h
1
′
=
h
2
+
h
3
+
h
5
h_1^{'} = h_2 + h_3 + h_5
h1′=h2+h3+h5
2.ConvGNNs
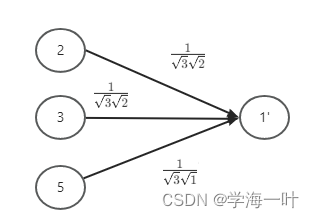
图卷积网络(GCN)就考虑到了节点的度,度越大,权重越小,使用了加权的SUM
[
h
1
′
h
2
′
h
3
′
h
4
′
h
5
′
]
=
[
0
1
3
2
1
3
2
0
1
3
1
⋮
⋮
⋮
⋮
⋮
]
∗
[
h
1
h
2
h
3
h
4
h
5
]
\begin{bmatrix} h_1^{'}\\h_2^{'}\\h_3^{'}\\h_4^{'}\\h_5^{'} \end{bmatrix} = \begin{bmatrix} 0&\frac{1}{\sqrt{3}\sqrt{2}}&\frac{1}{\sqrt{3}\sqrt{2}}&0&\frac{1}{\sqrt{3}\sqrt{1}}\\\vdots&\vdots&\vdots&\vdots&\vdots \end{bmatrix} * \begin{bmatrix} h_1\\h_2\\h_3\\h_4\\h_5 \end{bmatrix}
h1′h2′h3′h4′h5′
=[0⋮321⋮321⋮0⋮311⋮]∗
h1h2h3h4h5
可以看出,
h
1
′
=
1
3
2
h
2
+
1
3
2
h
3
+
1
3
1
h
5
h_1^{'} = \frac{1}{\sqrt{3}\sqrt{2}}h_2 + \frac{1}{\sqrt{3}\sqrt{2}}h_3 + \frac{1}{\sqrt{3}\sqrt{1}}h_5
h1′=321h2+321h3+311h5
3.GAT
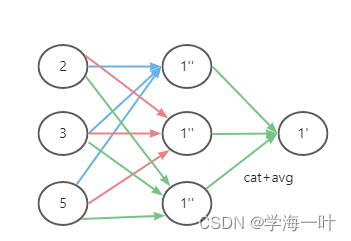
再到后面发展为图注意力网络GAT,在消息传递过程中引入了注意力机制: