二叉树基础

常见的二叉树。

两类特殊的二叉树，满二叉树和完全二叉树。
满二叉树即一棵节点满了的二叉树，想要再添加一个节点只能添加一层了。

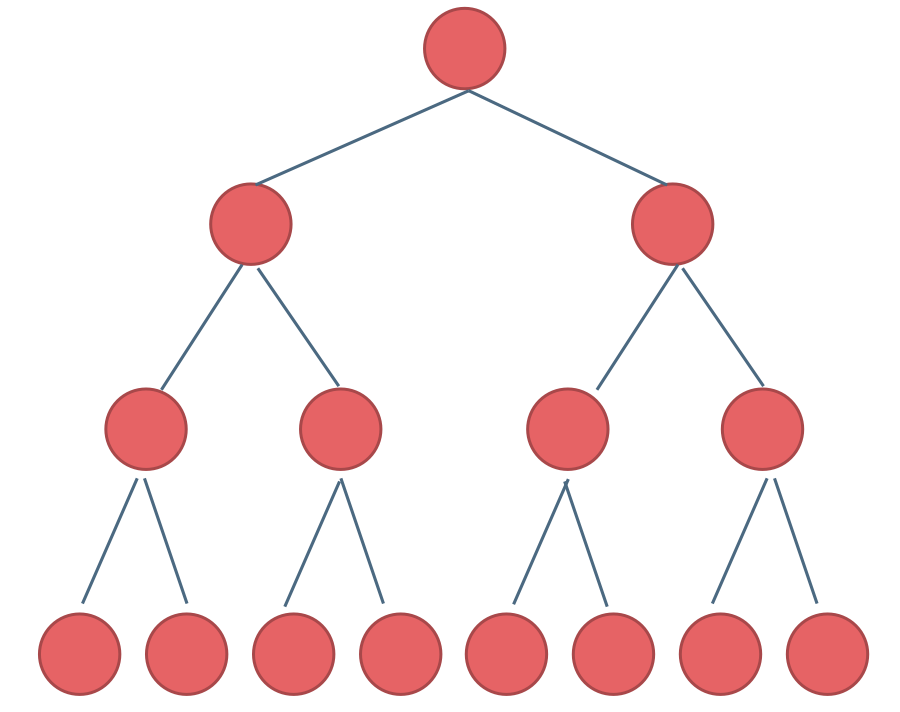
完全二叉树:照着满二叉树从上到下，从左到右的顺序添加节点，中间的过程都是完全二叉树。

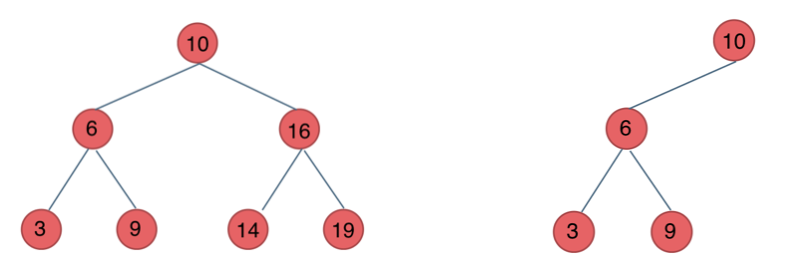
二叉搜索树
可以用来做二分搜索的树。满足左<根<右的性质。

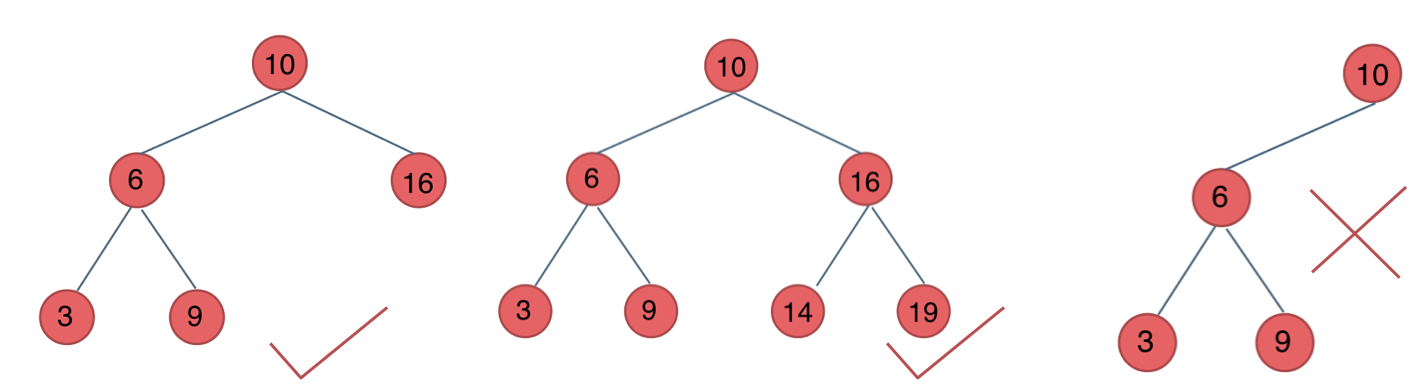
平衡二叉树
左右两个子树的高度差的绝对值不超过1

二叉树的遍历

递归遍历

递归三要素：

1. 函数参数和返回值
2. 终止条件
3. 单层递归逻辑

用三要素写前序遍历：

1. 参数和返回值。 前序遍历需要知道当前节点，还需要一个数组保存节点的值。不需要返回值。

def traversal(cur, vec):

2. 终止条件。 如果当前节点是空节点，则需要返回。

if not cur:
	return None

3. 单层递归逻辑。 单层的逻辑是，取根节点值，然后遍历左子树，遍历右子树。

vec.append(cur.val)
traversal(cur.left, vec)
traversal(cur.right, vec)

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def preorder(cur, vec):
            if not cur:
                return None
            vec.append(cur.val)
            preorder(cur.left, vec)
            preorder(cur.right, vec)
            
        vec = []
        preorder(root, vec)
        return vec 

改变一下遍历的顺序，可以写出中序遍历和后序遍历。
中序：

preorder(cur.left, vec)
vec.append(cur.val)
preorder(cur.right, vec)

后序：

preorder(cur.left, vec)
preorder(cur.right, vec)
vec.append(cur.val)

迭代遍历

使用栈来替代递归。

前序遍历。（根，左，右）
注意入栈顺序，用pop弹出栈顶元素（根）后，接着将右子树入栈，然后左子树入栈。这样出栈的时候才是根左右。

class Solution:  
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:  
        st = []  
        res = []  
        if root == None:  
            return res  
        st.append(root)  
        while (len(st)>0):  
            cur = st.pop()  
            res.append(cur.val)  
            if cur.right:  
                st.append(cur.right)  
            if cur.left:  
                st.append(cur.left)  
  
        return res

后序遍历（左，右，根）。只要在前序基础上调整一下， 对调 加入 右左孩子 顺序（得到根右左）， 并反转结果（左右根）。

class Solution:  
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:  
        res = []  
        st = []  
        if not root:  
            return res  
  
        st.append(root)  
        while (len(st) > 0):  
            cur = st.pop()  
            res.append(cur.val)  
            if cur.left:  
                st.append(cur.left)  
            if cur.right:  
                st.append(cur.right)  
  
        return res[::-1]

中序遍历比较特殊，因为访问和处理节点的顺序不一样。
使用指针cur 辅助访问节点。栈st用来处理节点。
如果cur不为None，就往左走，并且用st记录经过的节点。（访问过程）
如果cur为None了，cur = st.pop()弹出元素，处理数据（中），然后访问右。

class Solution:  
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:  
        res = []  
        if not root:  
            return res  
        st = []  
        cur = root  
        while cur or st:  
            if cur: # cur指针访问节点，直到最左  
               st.append(cur)  
               cur = cur.left # 左  
            else:  
                cur = st.pop() # 要处理的数据(根)  
                res.append(cur.val)  
                cur = cur.right # 右  
        return res

层序遍历

层序遍历是逐层访问。可以用队列实现，先确定当前层的节点数为length，然后遍历length次， 处理当前节点并添加节点的左右子节点。

from collections import deque
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        res = []
        if not root:
            return res
        queue  = deque()
        queue.append(root)
        while queue:
            sub_list  = []
            length = len(queue)
            for i in range(length):
                node = queue.popleft()
                sub_list.append(node.val)
                for nextnode in [node.left, node.right]:
                    if nextnode:
                        queue.append(nextnode)

            res.append(sub_list)
        return res