15.三数之和
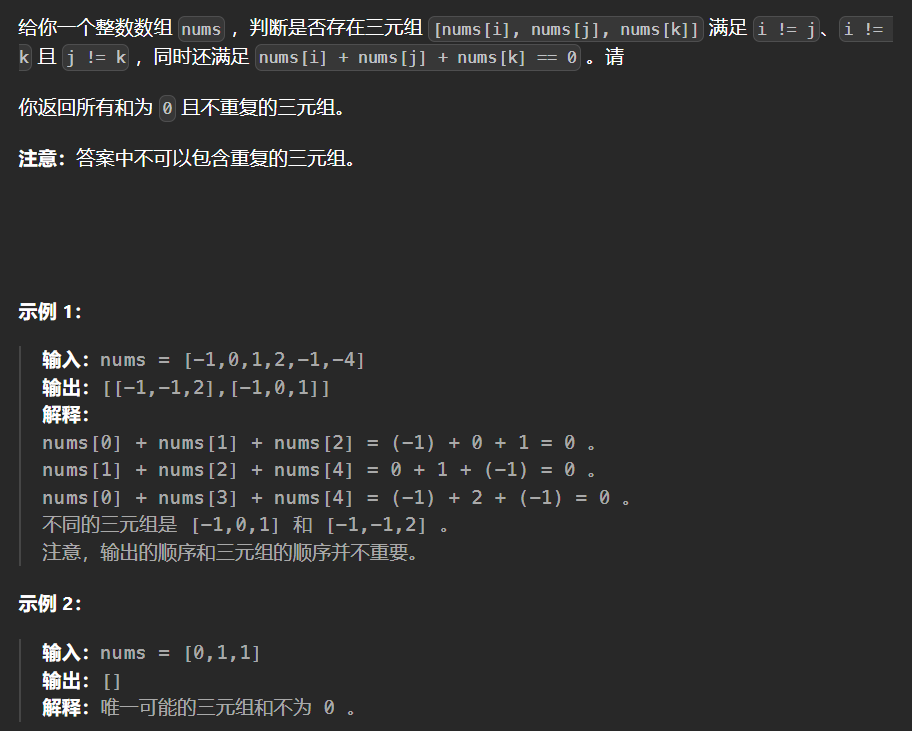
注意:最后答案中不能包含重复的三元组
使用排序+双指针
可以使用三重循环枚举三元组,但是需要哈希表进行去重操作,得到不包含重复三元组的最终答案,消耗量大量的时间和空间
对于不重复的本质,保持三重循环的大框架不变,只需要保证:
- 第二重循环枚举到的元素不小于当前第一重循环枚举到的元素
- 第三重循环枚举到的元素不小于当前第二重循环枚举到的元素
也就是说,我们枚举到的三元组(a,b,c)满足a≤b≤c,保证了只有(a,b,c)这个顺序会被枚举到,而(b,a,c)和(c,b,a)这些不会,这样就减少了重复,要实现这一点,可以将数组中的元素从小到大进行排序
同时,保证在每一重循环中,相邻两次枚举的元素不相同,避免重复
此时,时间复杂度仍未 O ( N 3 ) O(N^3) O(N3),仍然没有跳出三重循环的大框架,因此继续优化,进一步,如果我们固定了前两重循环枚举到的元素a和b,那么只有唯一的c满足a+b+c=0,当第二重循环往后枚举一个元素b’时,由于b’>b,那么满足a+b’+c’=0的c’一定有c’<c,即c‘在数组中一定出现在c的左侧,也就是说,我们可以从小到大枚举b,同时从大到小枚举c,即第二重循环和第三重循环实际上是并列的关系,这就是双指针:当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从 O ( N 2 ) O(N^2) O(N2)减少至 O ( N ) O(N) O(N)
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
int n = nums.length;
Arrays.sort(nums); //先对数组进行排序
List<List<Integer>> ans = new ArrayList<List<Integer>>();
//枚举a
for(int first = 0;first < n; first++){
//需要和上一次枚举的数不相同,只有和上一次枚举的元素不相同时,才会进行枚举
if(first > 0 && nums[first] == nums[first - 1]){
continue;
}
// c对应的指针指向数组的最右端
int third = n - 1;
int target = -nums[first];
// 枚举b
for(int second = first + 1;second<n;second++){
//同样需要和上一次枚举的元素不相同
if(second > first + 1 && nums[second] == nums[second -1]){
continue;
}
//保证b的指针在c的指针的左侧
while(second < third && nums[second] + nums[third] > target){
--third;
}
//如果指针重合,随着b后续的增加
// 就不会有满足a+b+c=0并且b<c了,可以退出循环
if(second == third){
break;
}
if(nums[second] + nums[third] == target){
List<Integer> list = new ArrayList<Integer>();
list.add(nums[first]);
list.add(nums[second]);
list.add(nums[third]);
ans.add(list);
}
}
}
return ans;
}
}