前言

本系列文章作为最优化学习的相关笔记。参考书目：文再文老师的《最优化：建模、算法与理论》

最优化问题概括

最优化问题的一般形式

最优化问题一般可以描述为：
$$\begin{array}{c}\begin{array}{r}\min f(x),\\ \text{s.t.}x\in \mathcal{X},\end{array}\end{array}$$
其中 $x=(x_1,x_2,\cdot \cdot \cdot ,x_n{)}^T\in {\mathbb{R}}^n$ 是决策变量，$f:{\mathbb{R}}_n\to \mathbb{R}$是目标函数，$\mathcal{X}\subseteq {\mathbb{R}}_n$ 是约束集合或可行域，可行域包含的点称为可行解或可行点．记号 s.t. 是 "subject to"的缩写，专指约束条件．当 $\mathcal{X}={\mathbb{R}}_n$ 时,问题(1)称为无约束优化问题.在所有满足约束条件的决策变量中，使目标函数取最小值的变量 $x^{\ast }$ 称为优化问题(1)的最优解，即对任意 $x\in \mathcal{X}$ 都有 $f(x)⩾f(x^{\ast })$．

PS:注意到在集合 $\mathcal{X}$ 上，函数 $f$ 的最小（最大）值不一定 存在，但是其下（上）确界"$\inf f(\sup f)$“总是存在的．因此，当目标函数 的最小 (最大）值不存在时，我们便关心其下（上）确界，即将问题(1)中的”$\min (\max )$“改为”$\inf (\sup )$"．

最优化问题的类型

• 当目标函数和约束函数均为线性函数时，线性规划；
• 当目标函 数和约束函数中至少有一个为非线性函数时，相应的问题称为非线性规划；
• 如果目标函数是二次函数而约束函数是线性函数则称为二次规划；
• 包含非光滑函数的问题称为非光滑优化；光滑函数之在其定义域内无穷阶连续可导的函数，比如说指数函数
• 不能直接求导数的问题称为无导数优化；
• 变量只能取整数的问题称为整数规划；
• 在线性约束下极小化关于半正定矩阵的线性函数的问题称为半定规划，其广义形式为锥规划．
• 按照最优解的性质来分：
  • 最优解只有少量非零元素的问题称为稀疏优化；
  • 最优解是低秩矩 阵的问题称为低秩矩阵优化

此外还有几何优化、二次锥规划、张量优化、 鲁棒优化、全局优化、组合优化、网络规划、随机优化、动态规划、带微分 方程约束优化、微分流形约束优化、分布式优化等.

例子：稀疏优化

考虑线性方程组求解问题：

$$\begin{array}{c}\begin{array}{r}Ax=b\end{array}\end{array}$$
其中向量 $x\in {\mathbb{R}}^n$，$b\in {\mathbb{R}}^m$，矩阵 $A\in {\mathbb{R}}^{m\times n}$，且向量 $b$ 的维数远小于向量 $x$的维数，即 $m\ll n$．方程组是欠定的，因此存在无穷多个解。如果加上稀疏性这一先验信息，且矩阵 $A$ 以及原问题的解 $u$ 满足某些条件，那么我们可以通过求解稀疏优化问题把 $u$ 与方程组 (2) 的其他解区别开．这类技术广泛应用于压缩感知（compressive sensing），即通过部分信息恢复全部信息的解决方案．

稀疏性等特征可以在理论上保证$u$ 是方程组 (2) 唯一的非零元素最少的解，即 $u$ 是如下 $l_0$ 范数问题的最优解：

$$\begin{array}{c}\begin{array}{r}\begin{array}{rl}\underset{x\in {\mathbb{R}}^n}{\min }& \Vert x{\Vert }_0,\\ \text{s.t.}& Ax=b.\end{array}\end{array}\end{array}$$
其中 $\Vert x{\Vert }_0$ 是指 $x$ 中非零元素的个数．由于$\Vert x{\Vert }_0$是不连续的函数，且取值 只可能是整数，问题 (2) 实际上是 NP（non-deterministic polynomial） 难的，求解起来非常困难。通过转化为$\Vert x{\Vert }_1$问题，则可以进行求解：
$$\begin{array}{c}\begin{array}{r}\begin{array}{rl}\underset{x\in {\mathbb{R}}^n}{\min }& \Vert x{\Vert }_1,\\ \text{s.t.}& Ax=b.\end{array}\end{array}\end{array}$$
但转化为2-范数，却无法求解。

原因：
在几何上，三种优化问题实际 上要找到最小的 $C$，使得"范数球" { x ∣ ‖ x ‖ ⩽ C } \{x|‖x‖ ⩽ C\} {x∣‖x‖⩽C}（$\Vert \cdot \Vert$ 表示任何一种范数）恰好与 $Ax=b$ 相交．下图为示意图：

PS:范数球是指在某个向量空间中，以某个向量为球心，以某个范数为半径所构成的球形集合。

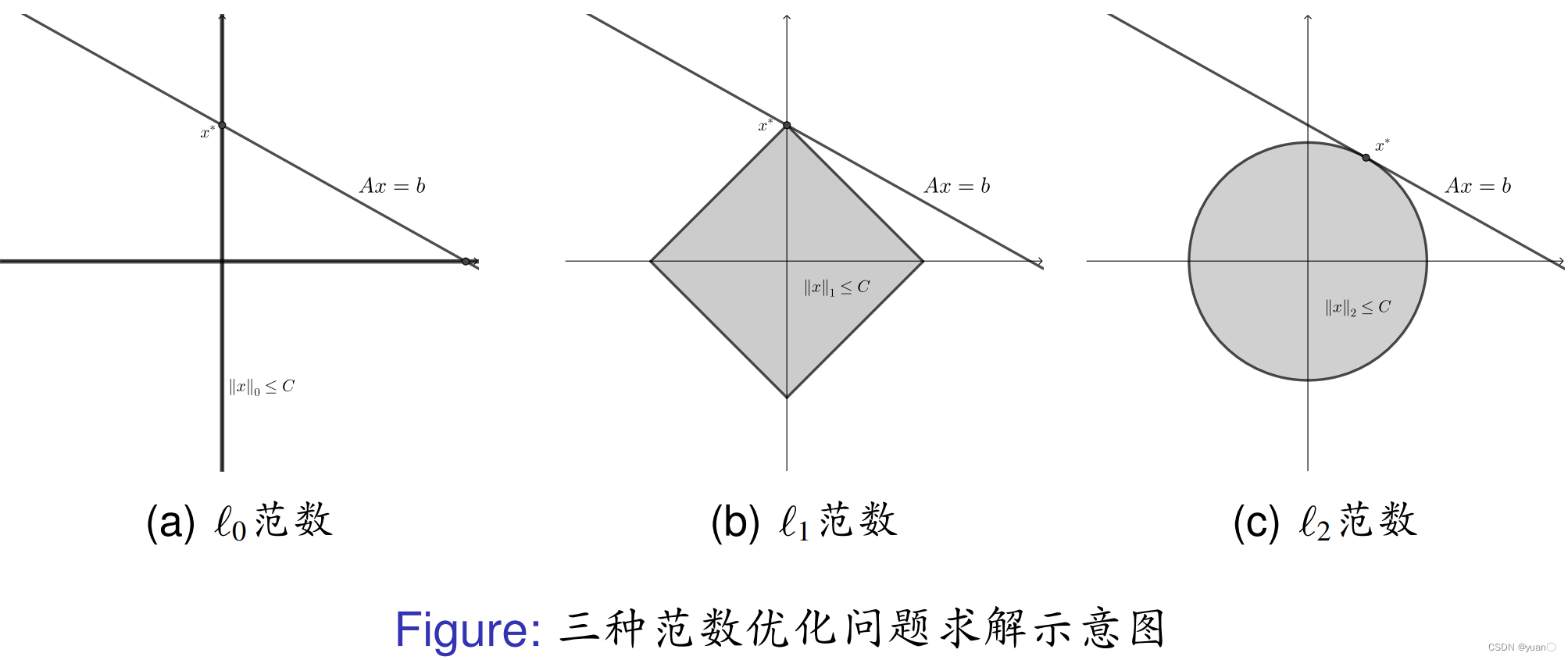
对 ${\ell }_0$范数，当 $C=2$ 时 { x ∣ ‖ x ‖ 0 ⩽ C } \{x|‖x‖0 ⩽ C\} {x∣‖x‖0⩽C} 是全平面，它自然与 $Ax=b$ 相交，而当$C=1$ 时退化成两条直线（坐标轴），此时问题的解是 $Ax=b$ 和这两条直线的交点；对 ${\ell }_1$ 范数，根据 $C$ 不同 { x ∣ ‖ x ‖ 1 ⩽ C } \{x|‖x‖1 ⩽ C\} {x∣‖x‖1⩽C} 为一系列正方形，这些正方形的顶点恰好都在坐标轴上，而最小的 $C$ 对应的正方形和直线 $Ax=b$的交点一般都是顶点，因此 ${\ell }_1$ 范数的解有稀疏性；对 ${\ell }_2$ 范数，当 $C$ 取值不同时 { x ∣ ‖ x ‖ 2 ⩽ C } \{x|‖x‖2 ⩽ C\} {x∣‖x‖2⩽C} 为一系列圆，而圆有光滑的边界，它和直线 $Ax=b$的切点可以是圆周上的任何一点，所以 ${\ell }_2$ 范数优化问题一般不能保证解的稀疏性．

$l_0$ 范数不是一个范数，这里为了叙述统一而采用了这个术语。
范数是数学中的一个概念，用来衡量向量的大小或长度。常用的范数有欧几里得范数、曼哈顿范数、切比雪夫范数等。

设 $x$ 是 $n$ 维向量 $(x_1,x_2,\cdots ,x_n{)}^{\top }$，则 $x$ 的范数
$\Vert x\Vert$ 定义为：

• 欧几里得范数（2-范数）：${\Vert x\Vert }_2=\sqrt{x_1^2+x_2^2+\cdots +x_n^2}$；
• 曼哈顿范数（1-范数）：${\Vert x\Vert }_1=\sum _{i=1}^n|x_i|$；
• 切比雪夫范数：${\Vert x\Vert }_{\infty }=\underset{1\le i\le n}{\max }|x_i|$。

范数的性质包括：

• 非负性：$\Vert x\Vert \ge 0$，且 $\Vert x\Vert =0$ 当且仅当 $x$ 是零向量；
• 齐次性或同次性：$\Vert \alpha x\Vert =|\alpha |\Vert x\Vert$，其中 $\alpha$ 是标量；
• 三角不等式：$\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert$；
• 自反性：$\Vert x\Vert =\underset{\Vert y\Vert \le 1}{\max }{x}^{\top }y$（对于切比雪夫范数），或
  $\Vert x\Vert =\underset{p\to \infty }{\lim }{\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}$（对于其他范数）。

${\ell }_1$ 范数正则项的优化问题 :
$$\begin{array}{c}\begin{array}{r}\underset{x\in {\mathbb{R}}^n}{\min }\mu \Vert x{\Vert }_1+\frac{1}{2}\Vert Ax-b{\Vert }_2^2,\end{array}\end{array}$$

其中 $\mu >0$ 是给定的正则化参数．问题 (5) 又称为 LASSO（least absolute shrinkage and selection operator），该问题可以看成是问题 (3)的二次罚函数形式．由于它是无约束优化问题，形式上看起来比问题 (3) 简单。

最优化的基本概念

全局和局部最优解

在求解最优化问题之前，先介绍最小化问题(1) 的最优解的定义．

如果一个点是局部极小解，但不是严格局部极小解，则称为非严格局部极小解。

优化算法收敛性

显式解：对于一个优化问题，如果我们能 用代数表达式给出其最优解，那么这个解称为显式解，对应的问题往往比较简单。

但实际问题往往是没有办法显式求解的，因此常采用迭代算法。

• 迭代算法的基本思想是：从一个初始点 $x_0$ 出发，按照某种给定的规则进行迭代，得到一个序列 $x_k$．如果迭代在有限步内终止，那么最后一个点就是优化问题的解．如果迭代点列是无穷集合，那么希望该序列的极限点（或者聚点）则为优化问题的解．
• 对于一个具体的算法，根据其设计的出点，我们不确定能得到一个高精度的近解。此时，为了避免无法使用的计算开销，我们还需要一些收敛标准来及时停算法进行。
• 在算法设计中，一个重要的标准是算法产生的点列是否收敛到优化问题的解。
• 考虑无约束的情形，对于一个算法，给定初始点 $x_0$，记其迭代产生的点列为 { x k } \{x_k\} {xk​}． 如果 { x k } \{x_k\} {xk​}在某种范数 $||\cdot ||$的意义下满足${\lim }_{k\to \infty }\Vert x^k-x^{\ast }\Vert =0,$且收敛的点 $x^{\ast }$ 为一个局部（全局）极小解，那么我们称该点列收敛到局部 （全局）极小解，相应的算法称为是依点列收敛到局部（全局）极小解的．
• 进一步地，如果从任意初始点 $x_0$ 出发，算法都是依点列收敛到局部（全局）极小解的，我们称该算法是全局依点列收敛到局部（全局）极小解的 ．相应地，如果记对应的函数值序列为 { f ( x k ) } \{f (x^k)\} {f(xk)}，我们还可以定义算法的（全局）依函数值收敛到局部（全局）极小值的概念．
• 对于凸优化问题，因为其任何局部最优解都为全局最优解，算法的收敛性都是相对于其全局极小而言的。
• 除了点列和函数值的收敛外，实际中常用的还有每个迭代点的最优性条件（如无约束优化问题中的梯度范数，约束优化问题中的最优性条件违反度等等）的收敛
• 对于带约束的情形，给定初始点 $x_0$，算法产生的点列 { x k } \{x_k\} {xk​}不一定是可 行的（即 { x k } \{x_k\} {xk​} ∈ $\mathcal{X}$ 未必对任意 $k$ 成立）．考虑到约束违反的情形，我们需要保证 { x k } \{x_k\} {xk​}在收敛到 $x^{\ast }$ 的时候，其违反度是可接受的．除此要求之外，算法的收敛性的定义和无约束情形相同．

在设计优化算法时，我们有一些基本的准则或技巧．对于复杂的优化问题，基本的想法是将其转化为一系列简单的优化问题（其最优解容易计算或 者有显式表达式）来逐步求解．常用的技巧有：

算法的渐进收敛速度

以点列的 $Q$-收敛速度（$Q$ 的含义为"quotient"）为例（函数值的 $Q$-收敛速度可以类似地定义）．设 { x k } \{x_k\} {xk​} 为算法产生的迭代点列且收敛于 $x^{\ast }$.

除 $Q$-收敛速度外，另一常用概念是 $R$-收敛速度（$R$ 的含义为"root"）

算法的复杂度

与收敛速度密切相关的概念是优化算法的复杂度 $N(\epsilon )$，即计算出给定 精度 $\epsilon$ 的解所需的迭代次数或浮点运算次数．