题目链接:654. 最大二叉树 - 力扣(LeetCode)
题目描述:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例:
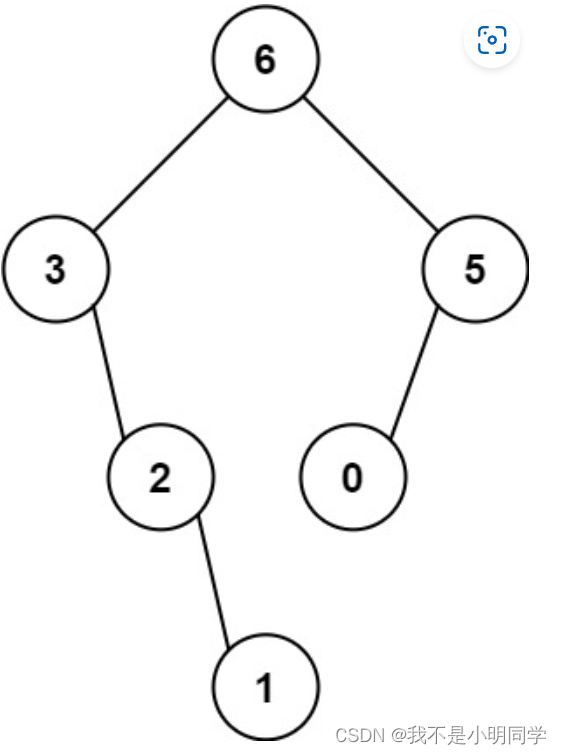
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
思路分析:题目中只给了一个数组 nums,那我们就根据这个 nums 数组结合二叉树的图来分析一下二者之间的关系。
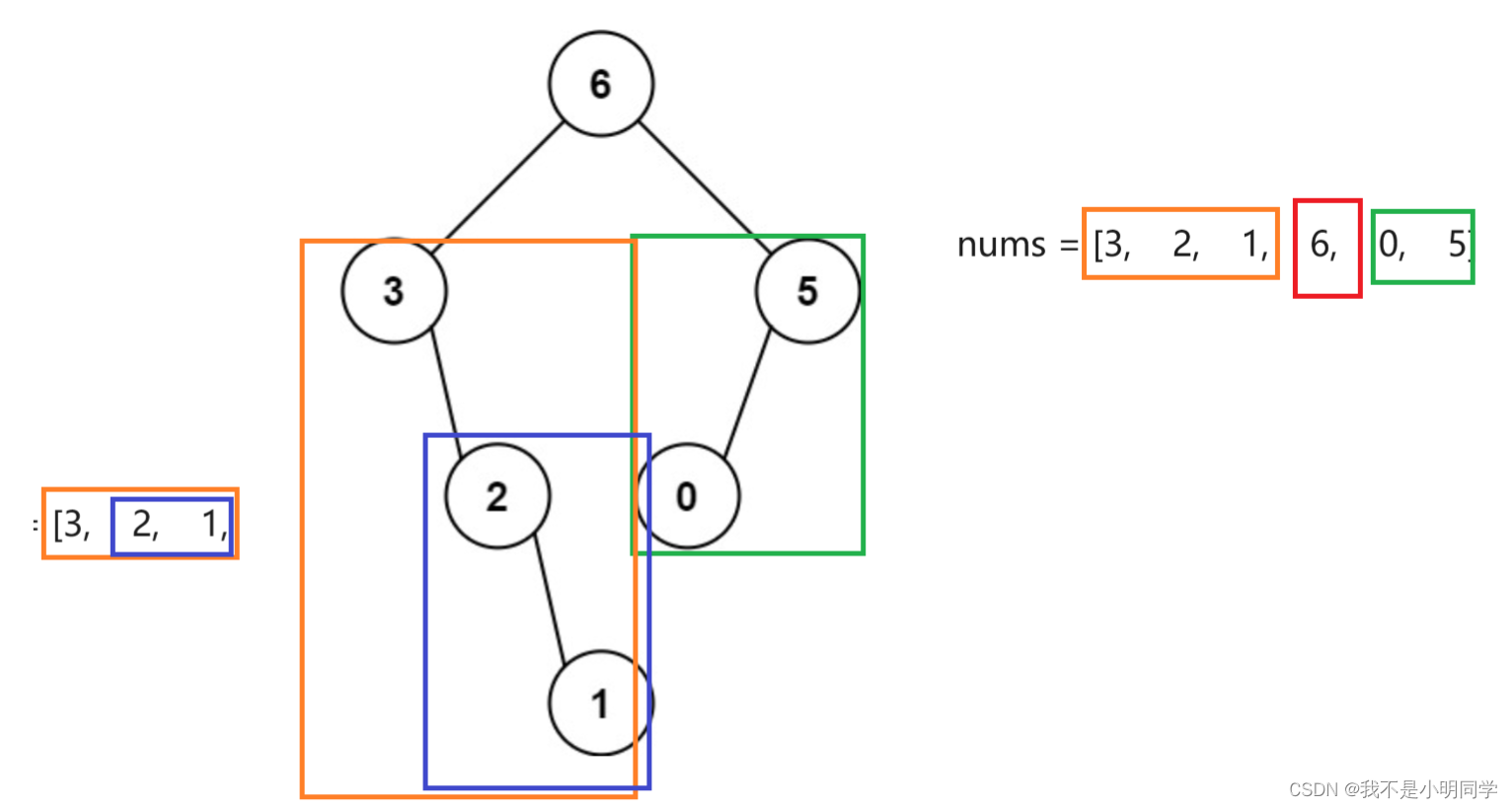
观察方框内的数据,不难看出,在数组中数据的分布和构造完成的二叉树的数据分布是相同的。我们可以总结出一个规律:在根节点左侧的数据就是根节点的左子树,在根节点右侧的数据就是根节点的右子树。有了这个规律我们接下来再构造最大二叉树的时候就可以大致分为三步:
1. 找到根节点的val 和 index;2. 根据根节点的 index 将数组分为左右两部分;3. 建造左子树和右子树。接下来我们详细分析一下这三个步骤。
1. 寻找根节点的 val 和 index,由题可知根节点是数组中最大的那个数据,也就是说,我们需要在数组中找到最大值及其下标。我们可以写一个方法,使它的返回值为数组,这样我们就可以一次获得数组中的最大值及其下标,将所得的最大值保存在根节点中。
2. 根据根节点的 index 划分数组,我们约定保存 val 和 index 的数组名为 indexVals,indexVals[0] 是 val,indexVals[1] 是 index,beg 是数组的开始,end 是数组的结尾,那么左子树部分就是 beg~indexVals[1]-1,右子树的部分就是 indexVals[1]+1~end。
3. 建造左子树和右子树,接下来我们只需要递归执行上述操作即可。
代码示例:
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
int len = nums.length-1;
return createTree(nums,0,len);
}
public TreeNode createTree(int[] nums,int beg, int end) {
if(beg > end) return null;
TreeNode root = new TreeNode();
// 寻找最大值及其下标
int[] indexVals = findIndex(nums,beg,end,-1,-1);
root.val = indexVals[0];
// 左子树,右子树
root.left = createTree(nums,beg,indexVals[1]-1);
root.right = createTree(nums,indexVals[1]+1,end);
return root;
}
public int[] findIndex(int[] nums,int beg, int end,int maxValue,int maxValueIndex) {
for(int i = beg; i <= end; i++) {
if(nums[i] > maxValue) {
maxValue = nums[i];
maxValueIndex = i;
}
}
int[] res = new int[2];
res[0] = maxValue;
res[1] = maxValueIndex;
return res;
}
}