一、题目描述

题目连接：有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

输出需求

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

二、题目思路

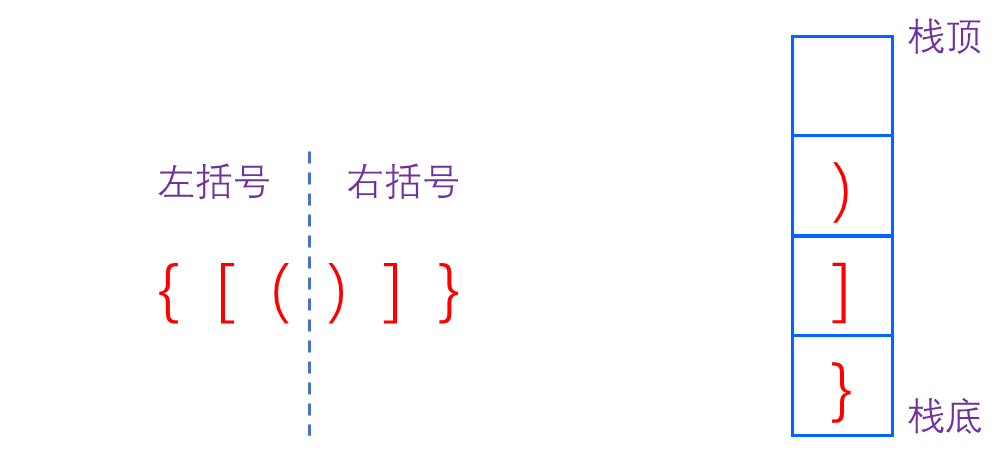
🍎 括号匹配是使用 栈 解决的经典问题，其思路如下：

遍历字符串，遇到左括号，将左括号与之对应的右括号入栈；将栈中的括号与右括号进行对比，一样就出栈。遍历完之后若栈为空，则字符有效， return ture .

🍐 在解决一些问题时，我们首先要考虑这些问题的极端性

🍉 首先分析不匹配的情况，一共有三种情况：

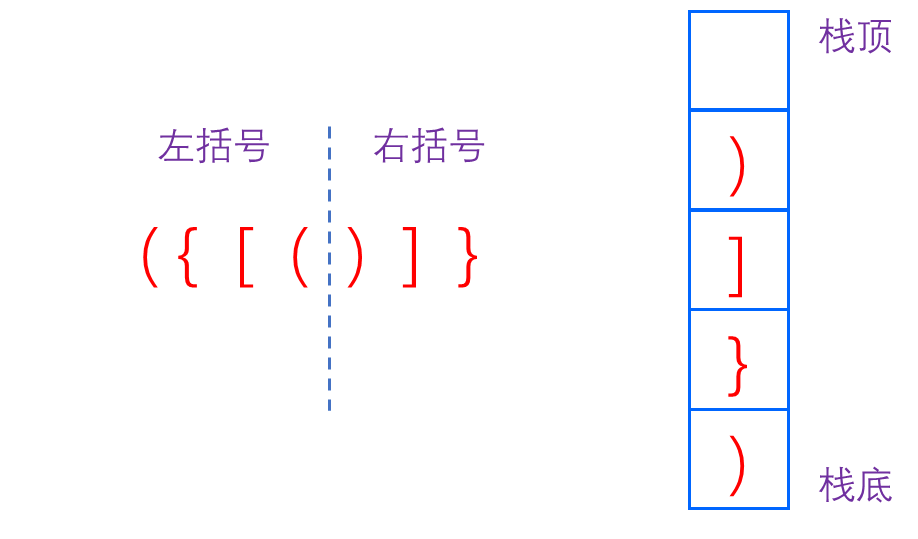
1️⃣：左括号多余

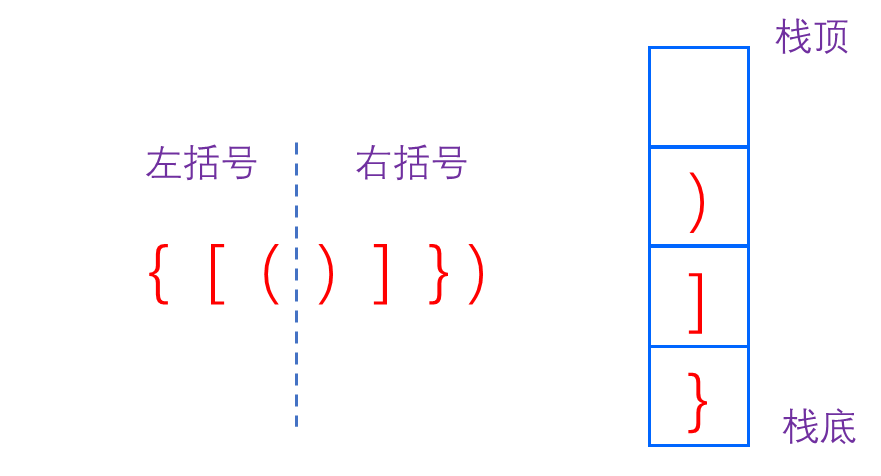
当遍历完字符串后栈不为空，则说明有多余的左括号，return flase.

2️⃣: 右括号多余

当遍历过程中遇到右括号时，栈为空，则说明右括号多余，return false.

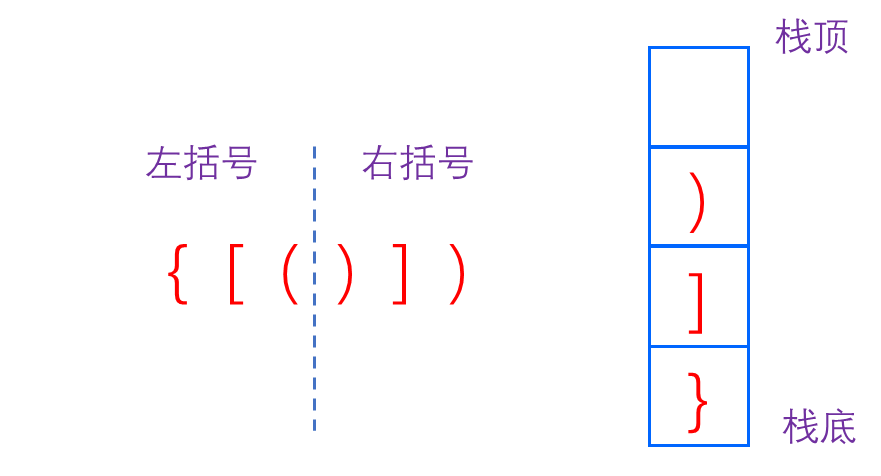
3️⃣: 括号没有多余，但是括号的类型没有对应上。

当遍历过程中遇到右括号时，栈顶元素与之不对应，则说明括号的类型没有对应上，return false.

三、问题实现

// 用栈解决
// 数组模拟栈
bool isValid(char * s)
{ 
    // 计算 原数组长度
    int len = strlen(s);
    // 先重新开辟一个动态数组来存储栈 （在堆上开辟）
    int* stack = (int*)malloc(sizeof(int)*len);
    // 记录插入栈中的数据个数
   int count = 0;        // 此时count指向的是栈中有效数据的下一个位置  也就是栈顶指针
   // 开始遍历整个数据
   for(int i = 0; i < len; i++)
   {
       // 开始遍历      先遍历左括号在遍历右括号
       if(s[i]=='(')
       {
           stack[count++] = ')';
       }
       else if(s[i]=='[')
       {
           stack[count++] = ']';
       }
       else if(s[i]=='{')
       {
           stack[count++] = '}';
       }
       // count=0 表示 右括号多余
       // stack[count-1]=s[i] 表示 类型没对上
       else if(count==0||stack[count-1]!=s[i])
       {
           return false;
       }
       else
       {
           count--;
       }
   }

   // 当遍历完整个数组，栈理应为空，如果栈没空 表示左括号多余
   return count==0;   //栈中无任何元素，说明全部匹配成功
}