周志华 《机器学习初步》 线性模型

还未更新完，会持续更新

一.线性回归

线性模型

线性模型的特点和重要性

• 线性模型的重要性

  • 人在考虑问题时，通常不是直接去思考一些非线性的问题。
  • 而考虑线性的问题，我们马上会有一个几何的直观的印象。基于这种几何直观的印象，我们可能能够从直观上得到一些解决方案，之后在线性模型的基础上可能得到针对非常复杂的非线性问题的解决方案

  

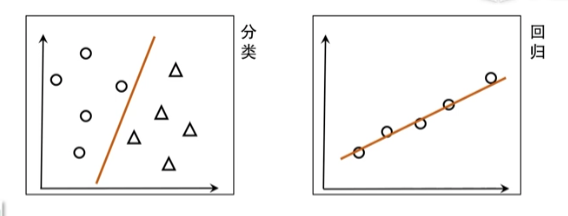
  • 比如要用线性模型去做分类和回归
    • 分类，找一条线把两类点分开
    • 回归，找一条线把点串起来

• 线性模型的特点：简单、基本、可理解性(understandability)/可解释性(comprehensibility)好

  • 线性模型形式简单、易于建模, 但却蕴涵着机器学习中一些重要的基本思想, 许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上 通过引入层级结构或高维映射而得
  • 此外, 由于 $\mathbf{w}$ 直观表达了各属性在预测中的重要性(权重), 因此线性模型有很好的可解释性
    • 例如若在西瓜 问题中学得 “ $f_{好瓜}(\mathbf{x})=0.2\cdot x_{\text{色泽 }}+0.5\cdot x_{\text{根蒂 }}+0.3\cdot x_{\text{敲声 }}+1$ ”, 则意味着可通过综合考虑色泽、根蒂和敲声来判断瓜好不好, 其中根蒂最要紧, 而敲声比色泽更重要.

线性模型的基本形式

• 给定由 d 个属性描述的示例 $\mathbf{x}=\left(x_1;x_2;\dots ;x_d\right)$, 其中 $x_i$ 是 $\mathbf{x}$ 在第 i 个属性上的取值, 线性模型(linear model)试图学得一个通过属性的线性组合来进行 预测的函数, 即
  $$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d+b,$$

• 一般用向量形式写成$f(\mathbf{x})={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b,$其中 $\mathbf{w}=\left(w_1;w_2;\dots ;w_d\right)$.

• $\mathbf{w}$ 和 $b$ 学得之后, 模型就得以确定.

参考资料

• 西瓜书🍉
• MOOC