Mysql概述

1.数据库相关概念

1.数据库：数据存储的仓库

2.数据库管理系统：操作和管理数据库的大型软件。（DBMS）

3.SQL：操作关系型数据库的编程语言，是一套标准。

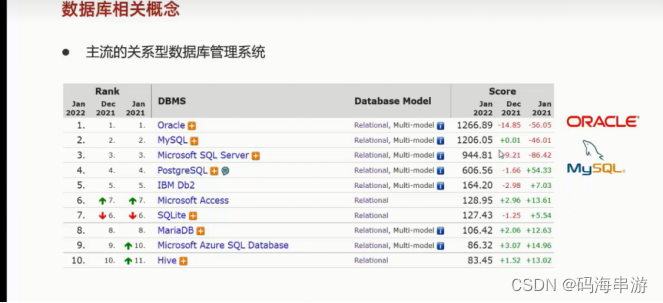
 都要使用SQL操作语言（统一标准）来操作

2.MySql数据库

版本：

社区版，免费但是不提供任何技术支持

商业版，提供技术支持。

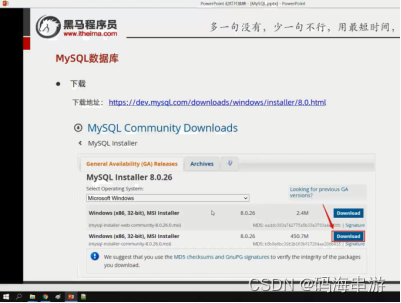
下载网址 mysql.com/downloads

SQL

启动与停止

1.在服务中启动与停止

2.用命令1，net start mysql80

               2,net stop mysql80

 3.配置环境变量

用cmd    输入命令 mysql -uroot -proot

函数

约束

多表查询

事务

未完，完了再说