基于WIN10的64位系统演示

一、写在前面

上一期，我们讲了单步滚动预测，一次只预测一个值。

既然有单步，有没有多步呢？那肯定有，这一期来介绍多步滚动预测。

然而，多步滚动模型也可以有不同的步骤，我会一一介绍。

2、多步滚动预测 vol-1

顾名思义，多步滚动预测就是使用前n个数值去预测下m个数值。假设，n = 3，m = 2，那么，之前举的例子就变成：使用三个数据点（1,2,3）来预测第4个和第5个数据点（4，5），使用三个数据点（2,3,4）来预测第5个和第6个数据点（5，6），使用三个数据点（3,4,5）来预测第6个和第7个数据点（6，7）。

输入	输出
1,2,3	4,5
2,3,4	5,6
3,4,5	6,7
...	...

发现没，这里有一个问题，预测的结果会出现重合。例如5，可以是（1,2,3）和（2,3,4）预测的结果，问题来了，我们选哪一个呢？

我想到两种方案：

（1）对于重复的预测值，取平均处理。例如，（1,2,3）预测出3.9和4.5，（2,3,4）预测出5.2和6.3，那么拼起来的结果就是3.9,（4.5 + 5.2）/2, 6.3。

（2）删除一半的输入数据集。例如，4,5由（1,2,3）预测，6,7由（3,4,5）预测，删掉输入数据（2,3,4）。

这一期，我们先试一试第一种策略吧。

2.1 数据拆分

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_absolute_error, mean_squared_error

data = pd.read_csv('data.csv')
data['time'] = pd.to_datetime(data['time'], format='%b-%y')

n = 6  # 使用前3个数据点
m = 2  # 预测接下来的2个数据点

# 创建滞后期特征
for i in range(n, 0, -1):
    data[f'lag_{i}'] = data['incidence'].shift(n - i + 1)

data = data.dropna().reset_index(drop=True)

train_data = data[(data['time'] >= '2004-01-01') & (data['time'] <= '2011-12-31')]
validation_data = data[(data['time'] >= '2012-01-01') & (data['time'] <= '2012-12-31')]

X_train = train_data[[f'lag_{i}' for i in range(1, n+1)]]

# 创建m个目标变量
y_train_list = [train_data['incidence'].shift(-i) for i in range(m)]
y_train = pd.concat(y_train_list, axis=1)
y_train.columns = [f'target_{i+1}' for i in range(m)]
y_train = y_train.dropna()
X_train = X_train.iloc[:-m+1, :]

X_validation = validation_data[[f'lag_{i}' for i in range(1, n+1)]]
y_validation = validation_data['incidence']

看看结果：

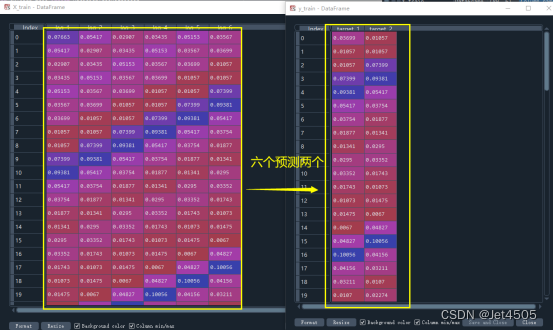
2.2 建模与预测

tree_model = DecisionTreeRegressor()
param_grid = {
    'max_depth': [None, 3, 5, 7, 9],
    'min_samples_split': range(2, 11),
    'min_samples_leaf': range(1, 11)
}

grid_search = GridSearchCV(tree_model, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)
best_params = grid_search.best_params_

best_tree_model = DecisionTreeRegressor(**best_params)
best_tree_model.fit(X_train, y_train)

# 预测验证集
y_validation_pred = []

for i in range(len(X_validation) - m + 1):
    pred = best_tree_model.predict([X_validation.iloc[i]])
    y_validation_pred.extend(pred[0])

# 重叠预测值取平均
for i in range(1, m):
    for j in range(len(y_validation_pred) - i):
        y_validation_pred[j+i] = (y_validation_pred[j+i] + y_validation_pred[j]) / 2

y_validation_pred = np.array(y_validation_pred)[:len(y_validation)]

mae_validation = mean_absolute_error(y_validation, y_validation_pred)
mape_validation = np.mean(np.abs((y_validation - y_validation_pred) / y_validation))
mse_validation = mean_squared_error(y_validation, y_validation_pred)
rmse_validation = np.sqrt(mse_validation)

print(mae_validation, mape_validation, mse_validation, rmse_validation)


# 拟合训练集
y_train_pred = []

for i in range(len(X_train) - m + 1):
    pred = best_tree_model.predict([X_train.iloc[i]])
    y_train_pred.extend(pred[0])

# 重叠预测值取平均
for i in range(1, m):
    for j in range(len(y_train_pred) - i):
        y_train_pred[j+i] = (y_train_pred[j+i] + y_train_pred[j]) / 2

y_train_pred = np.array(y_train_pred)[:len(y_train)]
mae_train = mean_absolute_error(y_train.iloc[:, 0], y_train_pred)
mape_train = np.mean(np.abs((y_train.iloc[:, 0] - y_train_pred) / y_train.iloc[:, 0]))
mse_train = mean_squared_error(y_train.iloc[:, 0], y_train_pred)
rmse_train = np.sqrt(mse_train)

print(mae_train, mape_train, mse_train, rmse_train)

解读：

这里的核心代码在于提取出重复值进行平均运算：

# 重叠预测值取平均

for i in range(1, m):

for j in range(len(y_validation_pred) - i):

y_validation_pred[j+i] = (y_validation_pred[j+i] + y_validation_pred[j]) / 2

y_validation_pred = np.array(y_validation_pred)[:len(y_validation)]

解释：

在多步滚动预测中，当我们每次都用前n个数去预测后面的m个数时，如果m大于1，那么就会出现预测值重叠的情况。为了具体解释哪些是重叠的数值，我们可以通过以下步骤来描述：

每次我们使用前n个数预测后m个数时，第一次预测的结果是为了得到下一个到第m个数值的预测。

当我们移动到下一个数据点并再次使用前n个数进行预测时，我们预测的第一个数值与上一次预测的第二个数值是相同的时间点的预测，因此它们是重叠的。同理，第二个数值与上一次预测的第三个数值重叠，依此类推。

所以，每次移动一个数据点并进行预测时，前m-1个预测结果都与上一次的预测结果存在重叠。

以n=3和m=2为例：

使用数据点1,2,3预测得到4和5。

使用数据点2,3,4预测得到5和6。

这里，两次预测中的数值5是重叠的。

为了判断哪些是重叠的数值，我们可以这样理解：在多次连续的预测中，除了第一次预测的结果，后面的每次预测的前m-1个数值都是与上次预测结果的最后m-1个数值重叠的。

在代码中，这正是为什么我们要有两层循环，外层循环i控制重叠的深度（从1到m-1），内层循环j则是遍历整个预测结果列表。

最后，看看结果吧：