一、贪心算法的思想

贪心算法是一种求解问题时，总是做出在当前看来是最好的选择，不从整体最优上加以考虑的算法。

二.用贪心算法的解题策略

其基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。贪心算法的关键在于贪心策略的选择，而不是对所有问题都能得到整体最优解。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。”

三典型题 

第五维度

零维是点，点动成线；

一维是线，线动成面；

二维是面，面动成体；

三维是体，体动成史；

四维是史，史动????

现在人类企图理解第五维度。

而小度现在是第五维度的一位智者。一天，小度发现人类的许多科学家在试图理解第五维度，人类是四维生物，若是他们理解了第五维度，很可能也会到来第五维度的空间，这显然是小度不愿意看到的（毕竟哪里都有人口数量的问题….）所以小度希望他们尽可能晚的理解第五维度，因此，小度用更高维度的视角把所有人类中在理解第五维的科学家都看到了，而这些科学家的智商会不一样，所以他们的理解速度 Vi​ 也会不一样；并且，他们开始理解的时间点 Si​ 也不一样。理解速度 Vi​ 描述为每过单位时间可获得 Vi​ 个单位理解力，也就是说在 Si​+1 的时间点该科学家会第一次贡献 Vi​ 的理解力。我们定义理解力总数超过m 时理解了第五维度。 小度因为维度更高，可以使用时间悖论来给人类一次重大的打击，小度可以让任意一位科学家在任意一个时间点消失，所以他接下来的理解不会继续；而且人类不会记得他，所以他之前的贡献会消失。因为小度能力有限，所以小度只能使用一次暂时悖论。

现在求在尽可能晚的情况下，人类理解第五维度的最早时间点。

时间点初始为00，但显然，没有科学家能够在 00 时刻有贡献。

格式

输入格式：

第一行给出一个整数 n 和一个整数 m ，表示有 n 个科学家，在理解力总数超过 m 时理解了第五维度；
第二至 n+1 行：每行两个整数Si​ 和 Vi​；
对于 100% 的数据：1≤n≤10^5，m≤2∗10^9；
对于 100% 的数据：00≤Si​≤2∗10^9，0≤Vi​≤10^3。

输出格式：

一行，包含一个整数 T 表示在尽可能晚的情况下，人类理解第五维度的最早时间点。
若是人类永远无法理解第五维度，则输出-1。

 

题解

 

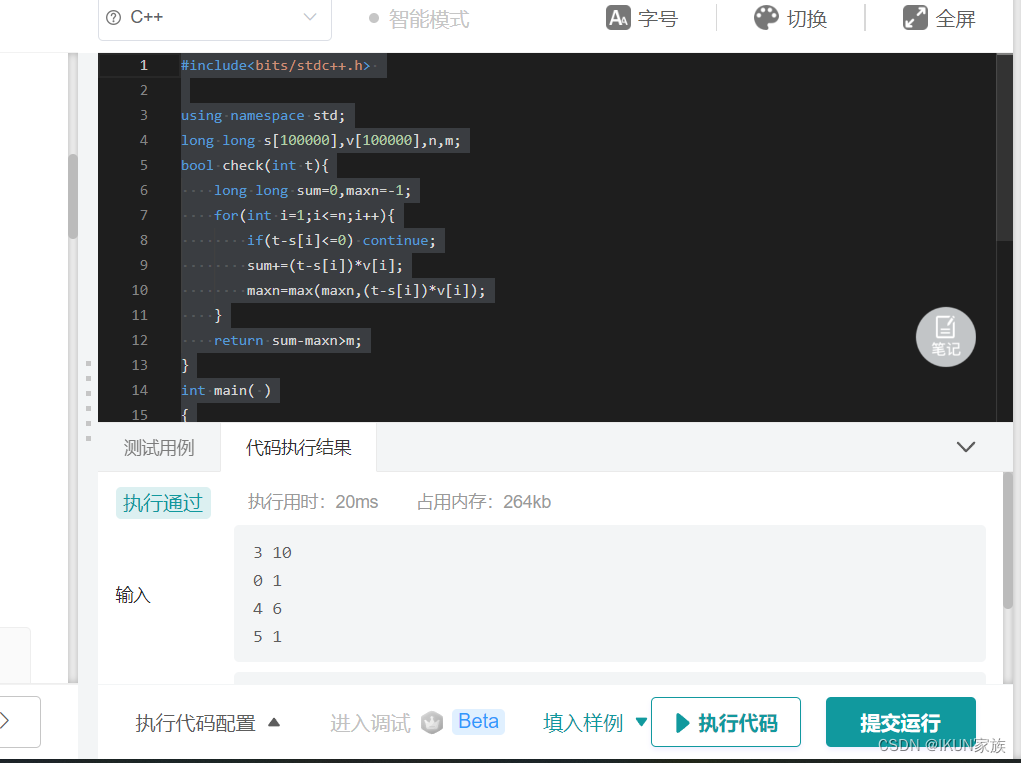
#include<bits/stdc++.h> 

using namespace std;
long long s[100000],v[100000],n,m;
bool check(int t){
    long long sum=0,maxn=-1;
    for(int i=1;i<=n;i++){
        if(t-s[i]<=0) continue;
        sum+=(t-s[i])*v[i];
        maxn=max(maxn,(t-s[i])*v[i]);
    }
    return sum-maxn>m;
}
int main( )
{
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>s[i]>>v[i];
    }
    int l=0,r=999999999;
    while(l<r){
        int mid=(l+r)/2;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    if(check(1)) cout<<l;
    else cout<<-1;
    return 0;
}

执行结果：