目录
1.数据的处理及查看
2.数据的处理及可视化
3.模型的创建与拟合
4.算法可视化效果图
5.多维度模型可视化
线性回归讲了很多次了,广义线性回归无非就是拟合的多项式曲线的次数的变化,就不再推导公式和算法流程了。
1.数据的处理及查看
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
#解决中文显示问题
plt.rcParams['font.sans-serif'] = ['KaiTi'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 从Excel读取数据
data = pd.read_excel('GeneralizedLinearRegression_data.xlsx')
data.head() 2.数据的处理及可视化
2.数据的处理及可视化
# 提取特征和标签
data=np.array(data)
X=data[:,0].reshape(-1,1)
y=data[:,1]
#绘制散点图大致看一下分布
plt.scatter(X,y,s=4)
plt.title("数据特征散点分布图")
plt.savefig(".\数据特征散点分布图.png",dpi=500)
plt.show()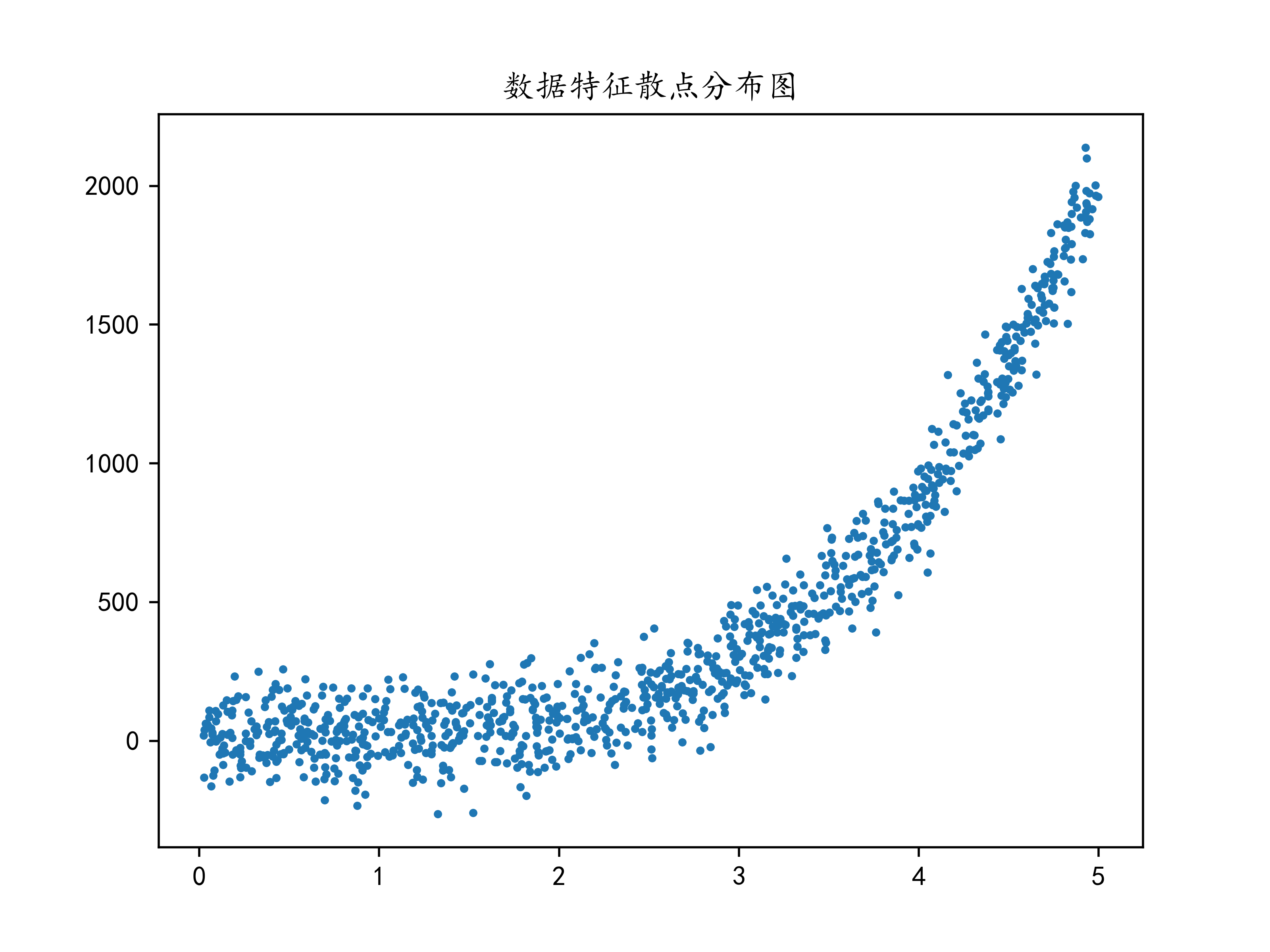
3.模型的创建与拟合
# 创建多项式特征
#根据图像来大致确定degree的值
poly = PolynomialFeatures(degree=4)
X_poly = poly.fit_transform(X)
# 创建线性回归模型
model = LinearRegression()
# 拟合模型
model.fit(X_poly, y)4.算法可视化效果图
# 生成一组连续的X值用于绘制回归曲线
X_test = np.linspace(X.min(), X.max(), 300).reshape(-1, 1)
X_test_poly = poly.transform(X_test)
# 预测值
y_test_pred = model.predict(X_test_poly)
# 绘制散点图和拟合曲线
plt.scatter(X, y, marker='.', label='Data',s=16)
plt.plot(X_test, y_test_pred, color='red',
label='Generalized_inear_Regression')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Generalized_Linear_Regression')
plt.legend()
plt.savefig(".\degree4_example.png",dpi=500)
plt.show()
5.多维度模型可视化
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 从Excel读取数据
data = pd.read_excel('GeneralizedLinearRegression_data.xlsx')
fig=plt.figure(figsize=(32,6))
fig.suptitle("不同维度的线性回归效果图",fontsize=13)
# 提取特征和标签
X = data[['x']].values
y = data['y'].values
# 利用for循环来进行进一步的
for i in range(8):
# 创建多项式特征
poly = PolynomialFeatures(degree=i+1)
X_poly = poly.fit_transform(X)
# 创建线性回归模型并且进行拟合模型
model = LinearRegression()
model.fit(X_poly, y)
# 生成一组连续的X值用于绘制回归曲线
X_test = np.linspace(X.min(), X.max(), 300).reshape(-1, 1)
X_test_poly = poly.transform(X_test)
# 预测值
y_test_pred = model.predict(X_test_poly)
# 绘制散点图和拟合曲线
plt.subplot(2,4,i+1)
plt.scatter(X, y, marker='.',color='blue', label='Data')
plt.plot(X_test, y_test_pred, color='red', label='Degree={}'.format(i+1))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.savefig(r"D:\HuaweiMoveData\Users\27182\Desktop\py\8维度回归图.png",dpi=500)
plt.show()
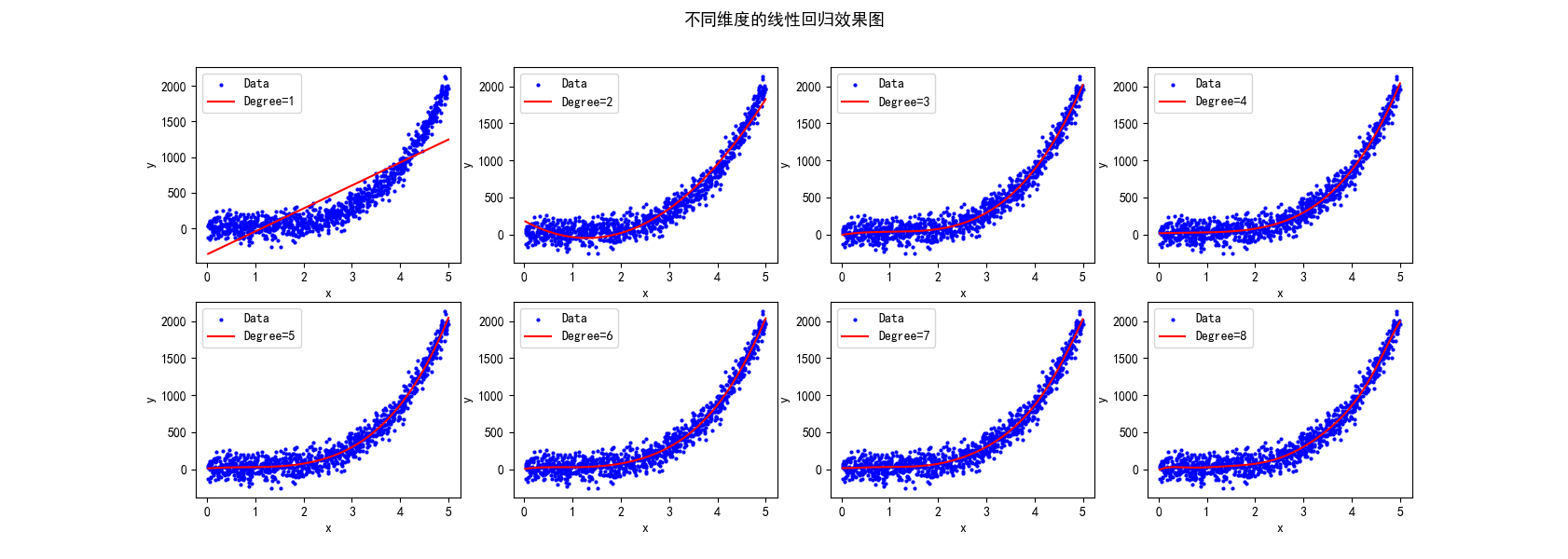
拟合的效果到最后都差不多了,n=4之后再增加就是徒增计算量了。