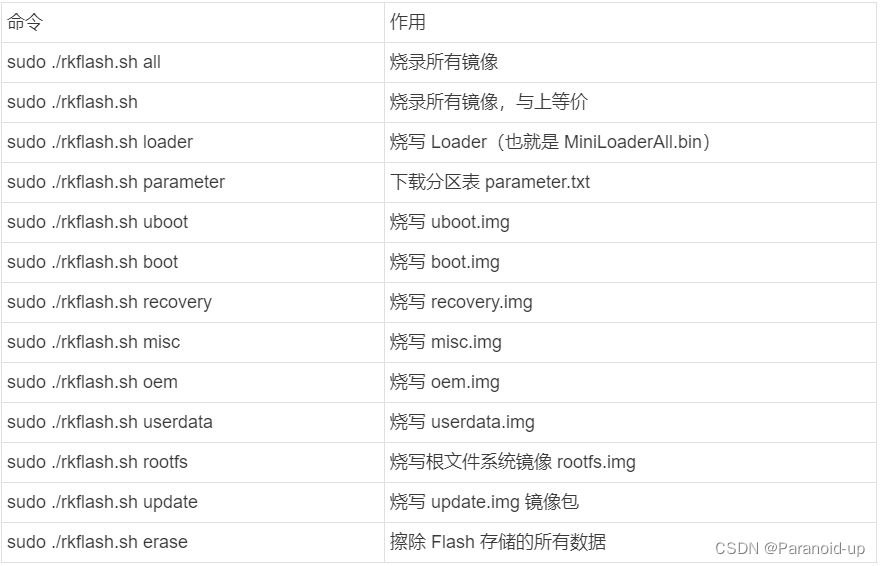
「信号与系统」语音信号的语谱图、尺度变化、带限处理、基音提取
本文将简单介绍几种语音信号的处理方法。
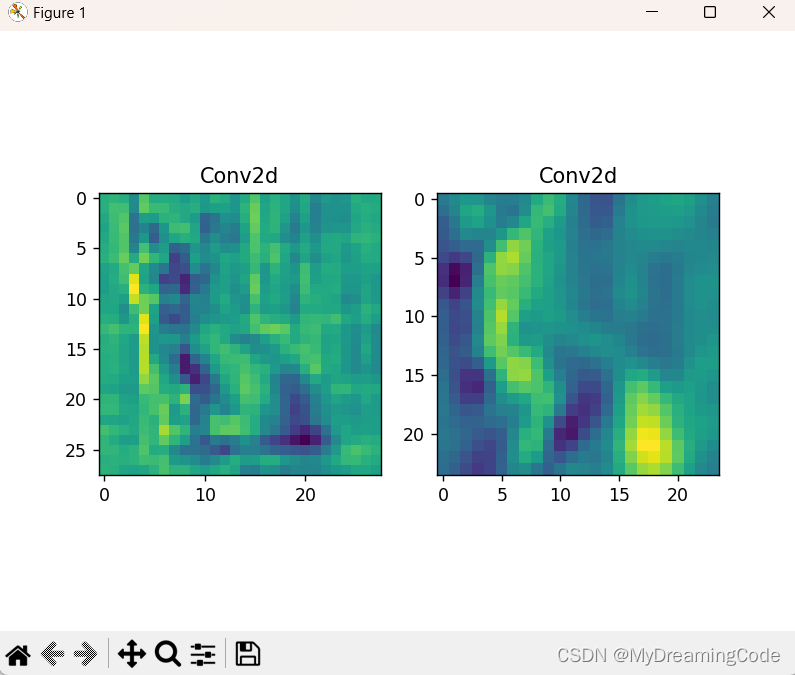
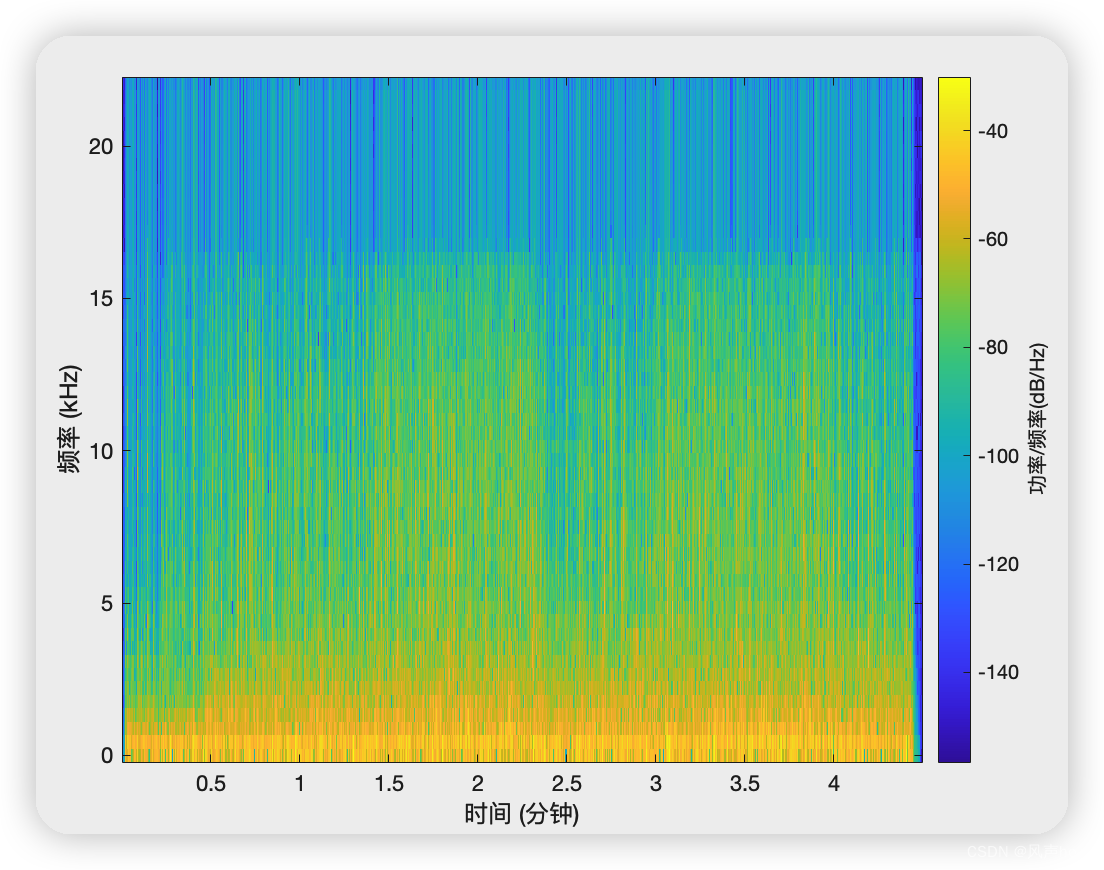
1、语谱图
语谱图是一种描述语音信号频率特征的方法,横轴表示时间,纵轴表示频率,颜色深浅表示能量。基本原理是将语音信号分帧(每帧10~30ms),对每一帧作fft求频谱,并按列绘制。以下是matlab代码,需要将音频文件放在同一个目录下面。
其中fs是采样频率,fs是数字世界和模拟世界的桥梁。众所周知,在计算机当中存储的是一个一个数字。比如《晴天》这首歌就是由11895852*2个双精度浮点数(实际存储的.mp3文件并非这样,要知道mp3是一种压缩格式)构成,两列分别表示左右声道。fs代表每秒钟对应多少个数,比如fs=44100,那么44100个点就代表1秒钟的数据。
[audioData,fs] = audioread("晴天_周杰伦.mp3");
spectrogram(audioData(:,1),100,80,100,fs,'yaxis')

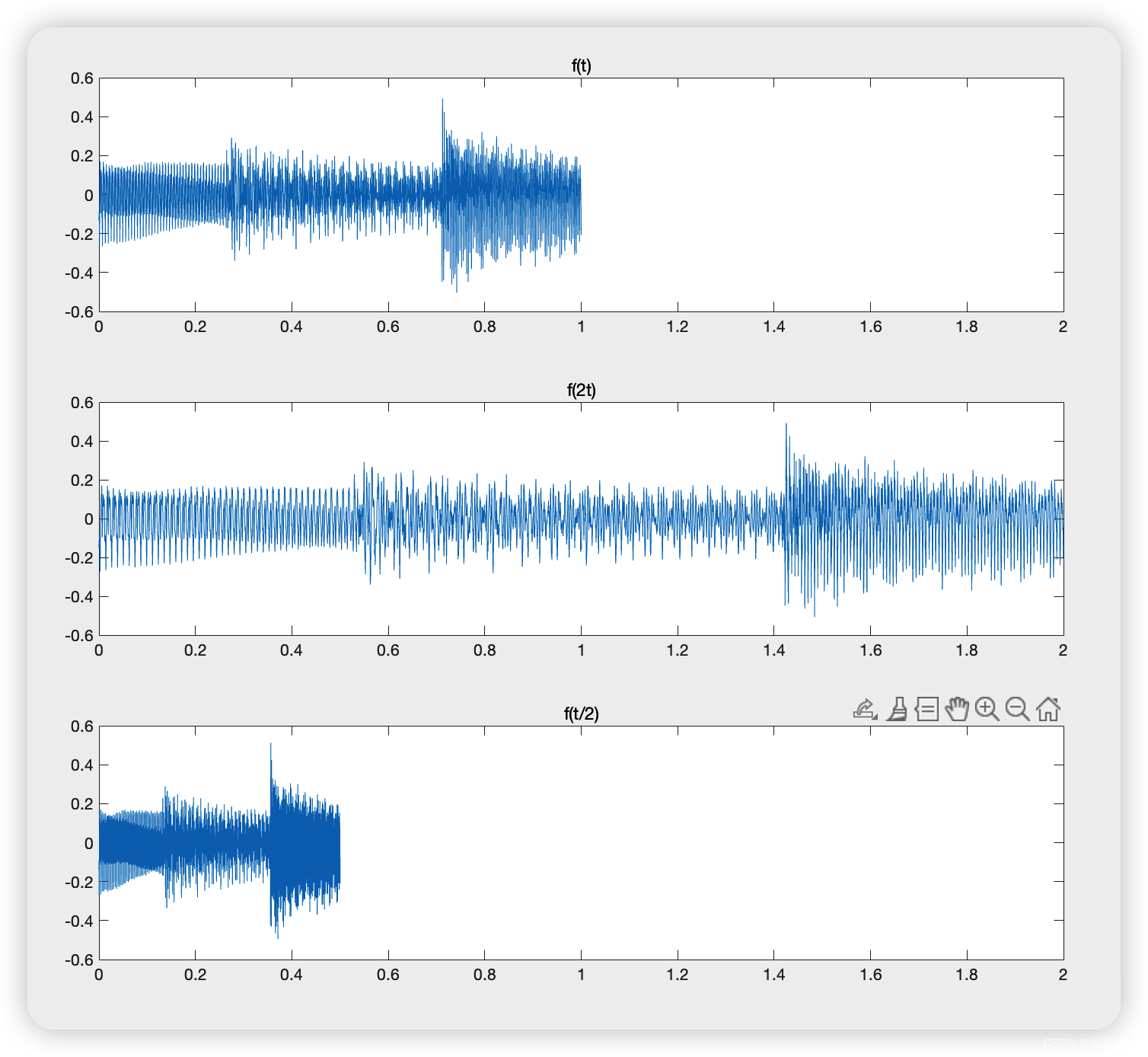
2、尺度变换
尺度变换,就是时间尺度变换。f(t)->f(2t’),表示用2t’来替换原来的t,那么在新的时间轴上,原来一分钟的歌,现在要播放两分钟。
在这里需要指出数字世界和模拟世界的不同。对于模拟信号,f(t)->f(2t’),假设f(t)=sin(t),那么f(2t’) = sin(t’/2),时间上无限稠密,因此可以采集到新的函数值。但是在数字世界,原来是[1,2,3,4] 变成新的[1,x,2,x,3,x,4,x],就不知道这个x应该是多少。为了解决这个问题,就引入了插值的概念(有的地方叫内插)。
反过来:f(t)->f(t’/2)。相对好解决些,因为[1,2,3,4]可以变成[1,3],直接舍弃掉2和4举行了。
下面用matlab作一个小实验:
[audioData,fs] = audioread("晴天_周杰伦.mp3");
f_t = audioData(fs+(1:fs),1);
f_2t = resample(f_t,2,1); % t->2t
f_t2 = resample(f_t,1,2); % t->t/2
%
% % 播放三段音频
% sound(f_t,fs)
% sound(f_2t,fs)
% sound(f_t2,fs)
% subplot
subplot(311)
plot((0:fs-1)/fs,f_t)
xlim([0,2]);title("f(t)")
subplot(312)
plot((0:fs*2-1)/fs,f_2t)
xlim([0,2]);title("f(2t)")
subplot(313)
plot((0:fs/2-1)/fs,f_t2)
xlim([0,2]);title("f(t/2)")
3、带限处理
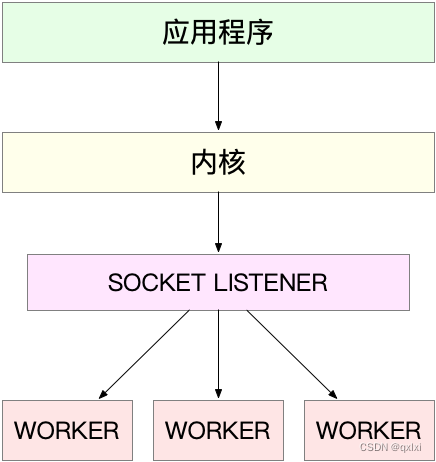
带限处理就是通过让音频信号通过一个滤波器,将其频带限制在我们设计的范围内。关于数字滤波器的种类、设计方法是一个十分复杂的知识体系,在此仅简要介绍。从是否有反馈回路,可分为IIR(无限冲激响应,有反馈回路)和FIR(有限冲激响应,无反馈回路,传递函数的相位是线性的)。从功能上分为四类:低通、高通、带通、带阻。
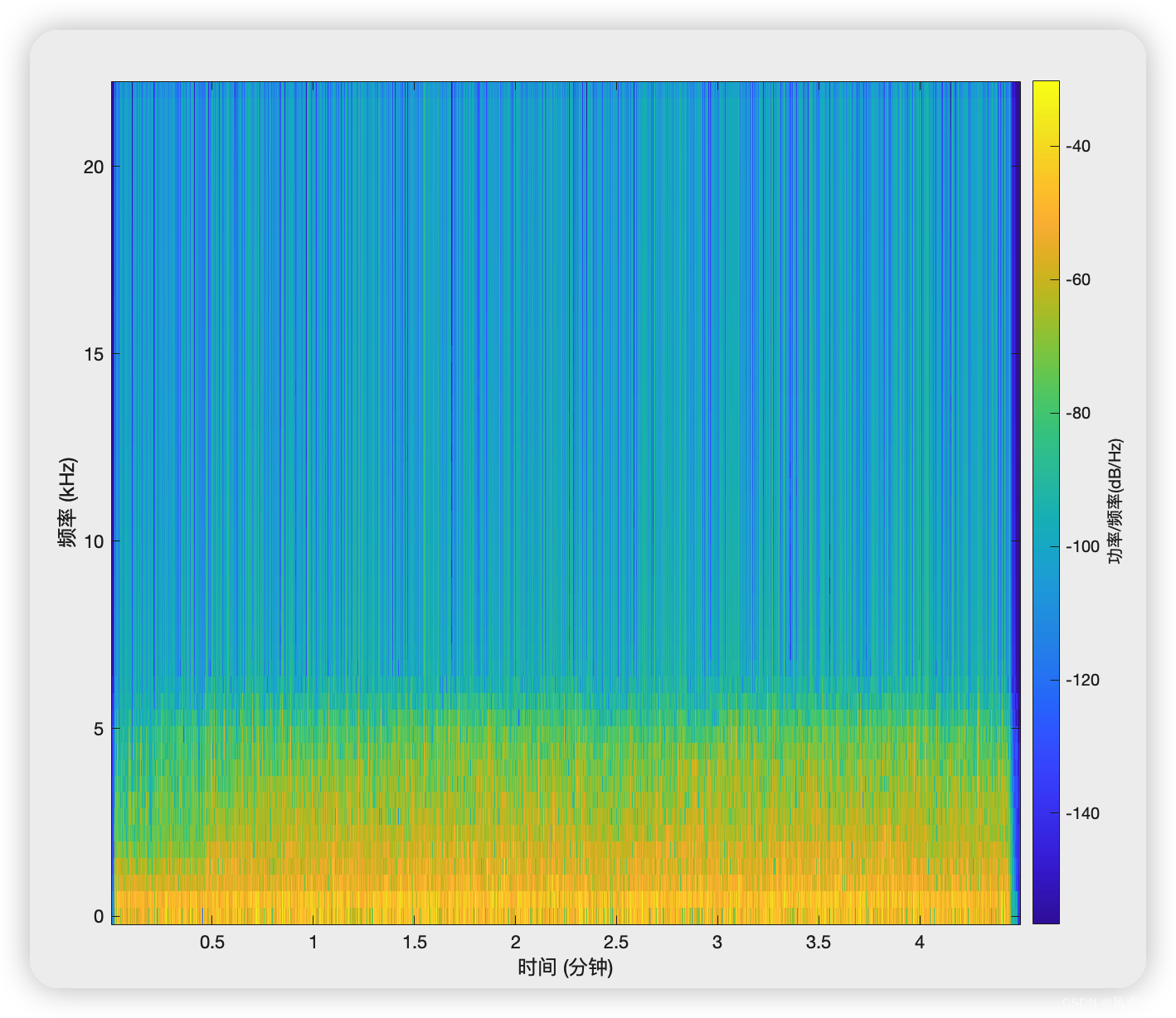
比如我可以设计一个通带截止频率为5kHz的48阶低通滤波器,将高频分量滤除:(对比两张语谱图可知高频分量被有效抑制了)
[audioData,fs] = audioread("晴天_周杰伦.mp3");
fp = 5000;
wn = fp/(fs/2); %归一化频率,1对应pi rad,pi rad对应fs/2
b = fir1(48,wn,'low');
audioData_lowpass = filter(b,1,audioData(:,1));
spectrogram(audioData_lowpass,100,80,100,fs,'yaxis')
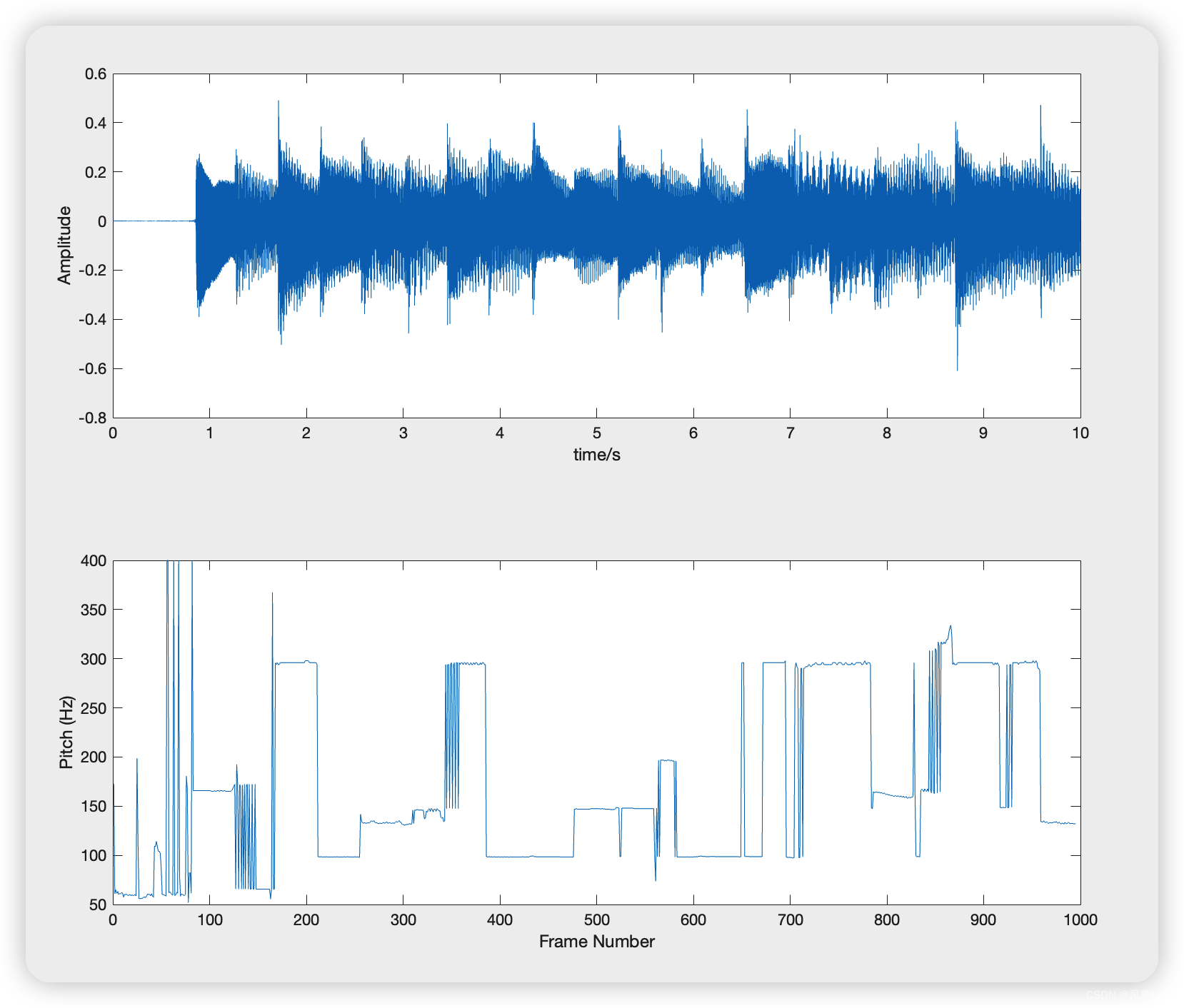
4、基音提取
令sin(w0t)为基波,则2w0、3w0、4w0……为其谐波,谐波的频率是基波的整数倍。直观上,一个语音信号频谱图的包络,其最高峰就是其基音频率。比较经典的基音估计算法有:基于短时自相关函数的基音周期估计和基于短时平均幅度差的基音周期估计。
下面是使用短时自相关函数的基音周期估计。
[audioData,fs] = audioread("晴天_周杰伦.mp3");
f_t = audioData((1:fs*10),1);
f0 = pitch(f_t,fs);
tiledlayout(2,1)
nexttile
plot((0:fs*10-1)/fs,f_t)
xlabel('time/s')
ylabel('Amplitude')
nexttile
plot(f0)
xlabel('Frame Number')
ylabel('Pitch (Hz)')