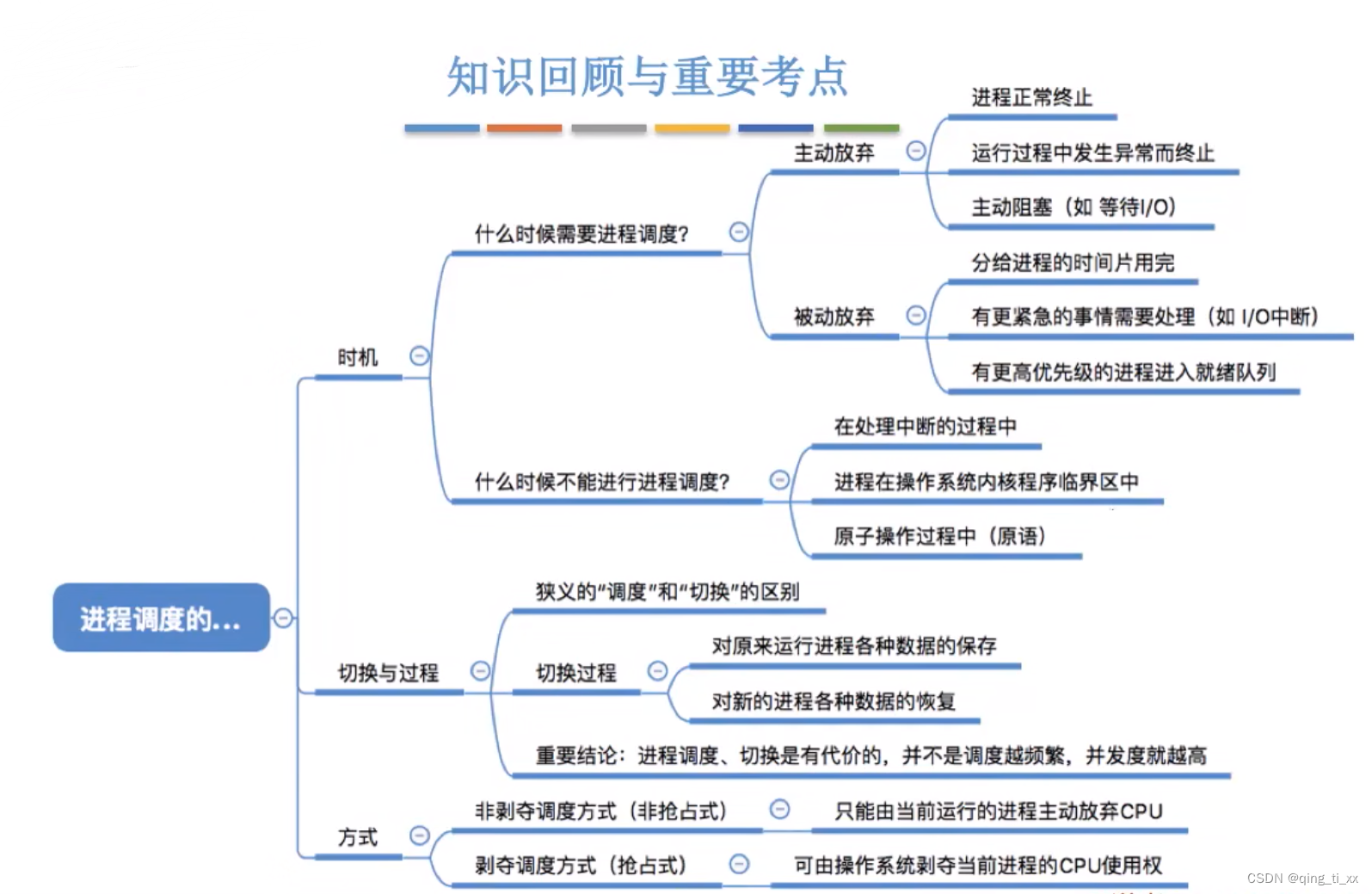
今天的三道题目，都算是 重叠区间 问题，大家可以好好感受一下。 都属于那种看起来好复杂，但一看贪心解法，惊呼：这么巧妙！ 

还是属于那种，做过了也就会了，没做过就很难想出来。

不过大家把如下三题做了之后， 重叠区间 基本上差不多了

 435. 无重叠区间 

与引爆气球相似，差不多；

代码随想录

public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals, (a,b)-> {
            return Integer.compare(a[0],b[0]);
        });
        int remove = 0;
        int pre = intervals[0][1];
        for(int i = 1; i < intervals.length; i++) {
            if(pre > intervals[i][0]) {
                remove++;
                pre = Math.min(pre, intervals[i][1]);//重点
            }
            else pre = intervals[i][1];
        }
        return remove;
    }
时间复杂度：O(nlog n) ，有一个快排
空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间

 763.划分字母区间 

代码随想录

时间复杂度：O(n)
空间复杂度：O(1)，使用的hash数组是固定大小

public List<Integer> partitionLabels(String S) {
        List<Integer> list = new LinkedList<>();
        int[] edge = new int[26];
        char[] chars = S.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            edge[chars[i] - 'a'] = i;
        }
        int idx = 0;
        int last = -1;
        for (int i = 0; i < chars.length; i++) {
            idx = Math.max(idx,edge[chars[i] - 'a']);
            if (i == idx) {
                list.add(i - last);
                last = i;
            }
        }
        return list;
    }

 56. 合并区间  

本题相对来说就比较难了。

代码随想录

本题的本质其实还是判断重叠区间问题。

大家如果认真做题的话，话发现和我们刚刚讲过的452. 用最少数量的箭引爆气球 (opens new window)和 435. 无重叠区间 (opens new window)都是一个套路。

这几道题都是判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重贴后要进行区间合并。

所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）

public int[][] merge(int[][] intervals) {
        LinkedList<int[]> res = new LinkedList<>();
        Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
        res.add(intervals[0]);
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] <= res.getLast()[1]) {
                int start = res.getLast()[0];
                int end = Math.max(intervals[i][1], res.getLast()[1]);
                res.removeLast();
                res.add(new int[]{start, end});
            }
            else {
                res.add(intervals[i]);
            }         
        }
        return res.toArray(new int[res.size()][]);
    }