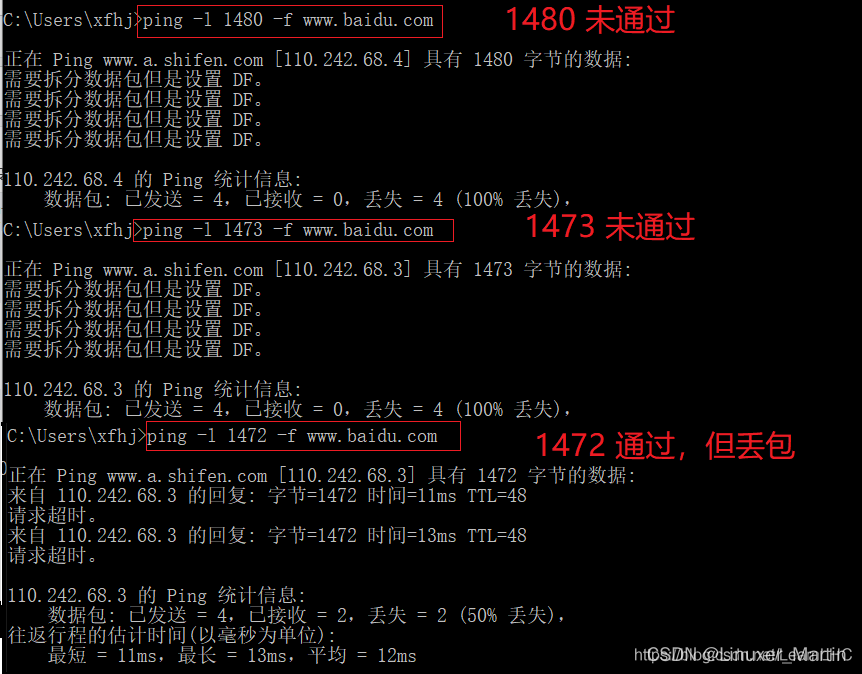
如何从第一性原则的原理分解数学问题
摘要:牛津大学入学考试题目展示了所有优秀数学家都使用的系统的第一原则推理,而GPT4仍然在这方面有困难
作者:Keith McNulty
我们中的许多人都熟悉直角三角形的边的规则。根据毕达哥拉斯定理,如果a和b是两条较短的边,c是最长的边,那么a² + b² = c²。
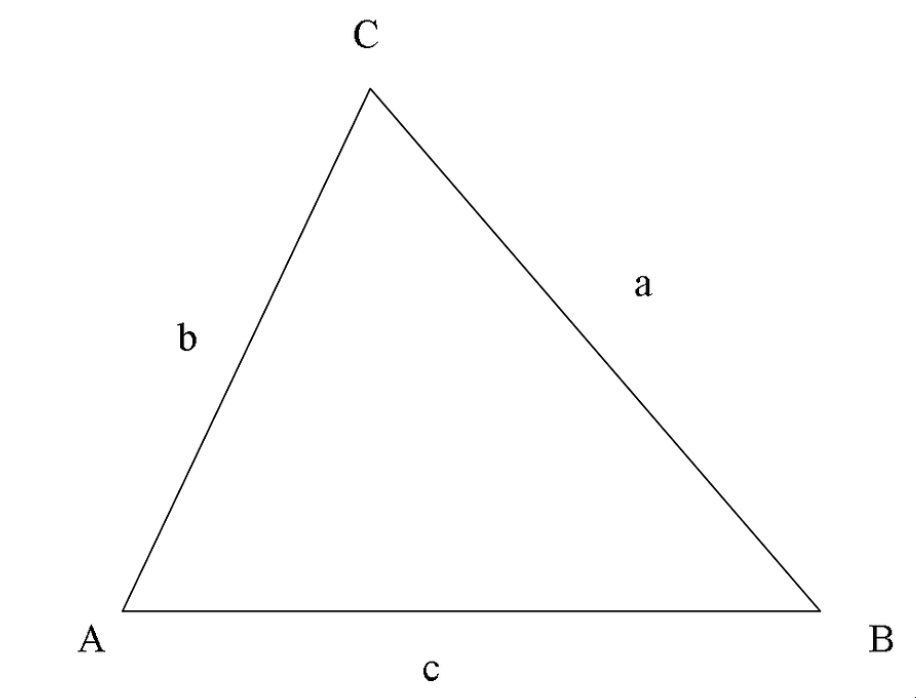
已知的整数解称为毕达哥拉斯三元组。例如,(3, 4, 5) 和 (5, 12, 13) 就是其中的一些。
更一般的构造是三元组。任何一组可以构成三角形的正整数三元组都称为三元组。
显然,整数毕达哥拉斯三元组也是三元组。但通常情况下,如果一个整数三元组 (a, b, c) 在(非严格)递增的顺序列出时,前两个整数的和严格大于第三个整数,那么它就是一个三元组。
以 (4, 2, 3) 为例。这些可以是三角形的边长,因为2 + 3 > 4。类似地,(2, 2, 2) 是一个三元组。但 (1, 3, 1) 不是三元组,因为无法用这些边长构建三角形(1 + 1 ≯ 3)。
最近牛津大学入学考试的一个问题涉及到三元组,我认为它很好地说明了如何逐步从第一原则分解问题,以解决起初看起来非常具有挑战性的问题。
这个问题定义了一个函数 f(P),其中 P > 2,表示三元组的数量,它们的和为 P。最后,它要求我们找到 f(21)。
找到和为 21 的三元组的数量似乎是一个真正的智力挑战,但是使用一些逐步的系统步骤,我们可以找到一个非常简单的计算方法。
最后,我还将展示像GPT4这样的人工智能在需要第一原则推理的这类问题上存在真正的问题。
以下是问题的各个部分和我的解决方案。我发现这是一个有趣的问题,是数学思维的很好练习,几乎不需要课本知识。
(i) 找到 f(3), f(4), f(5), f(6) 的值 这只是让我们适应思考和理解一个新概念。
由于唯一的正整数三元组,其和为三,是 (1, 1, 1),而且这显然是一个三元组,所以 f(3) = 1
任何和为 4 的正整数三元组都必须包含2。因此,另外两个数字都是1。由于1 + 1 不严格大于 2,所以不存在三元组,因此 f(4) = 0。
任何和为 5 的正整数三元组都必须包含2或3,但不能同时包含。如果它包含3,那么其他两个必须都是1,而这不是三元组。如果它包含2,那么其他两个必须是1和2,这是一个三元组。
因此,(2, 2, 1),(2, 1, 2) 和 (1, 2, 2) 都是这样的三元组,所以 f(5) = 3。
任何和为 6 的正整数三元组必须包含一个4和两个1(不是三元组),一个3、2和1各一个(不是三元组),或者三个2(是三元组)。
因此,唯一的三元组是 (2, 2, 2),因此 f(6) = 1。
(ii) 如果 (a, b, c) 是一个三元组,证明 (a+1, b+1, c+1) 也是一个三元组
首先注意,我们总是可以假设 a, b, c 是(非严格)递增的顺序,因为如果它们不是,我们可以简单地重新排列它们,使它们变成递增的。
这种推理在这个问题的大多数部分都很重要。
现在,由于 a+b > c,我们可以说 (a+1) + (b+1) = (a+b)+2 > c+2 > c+1。因此,(a+1, b+1, c+1) 是一个三元组。
(iii) 如果 (x, y, z) 是一个三元组,x+y+z 是偶数且不小于 6,证明 x, y 和 z 都至少为 2,并且 (x-1, y-1, z-1) 也是一个三元组
再次假设 x, y, z 是递增的。为了证明它们都至少为 2,我们只需要证明 x 不能为 1。假设 x = 1。然后 1+y+z 是偶数,所以 y+z 是奇数。
此外,我们有 1+y > z,所以 y > z -1,因此 y ≥ z。但我们知道 y ≤ z,因此 y = z。所以 y+z 是偶数。
这是一个矛盾,所以 x > 1。
(iv) 证明对于任何大于等于 3 的正整数 k,f(2k-3) = f(2k) 根据第二部分,我们知
道任何和为 2k-3 的三元组都可以通过简单地对每个整数加 1 映射到和为 2k 的三元组。
这意味着和为 2k 的三元组集合至少和和为 2k-3 的三元组集合一样大。
根据第三部分,由于 2k 是偶数且不小于 6,我们知道我们可以通过从每个整数中减去 1 来将和为 2k 的三元组唯一映射到和为 2k-3 的三元组。
这意味着和为 2k-3 的三元组集合至少和和为 2k 的三元组集合一样大。
因此,两个集合必须具有相同的大小,因此 f(2k-3) = f(2k)。
(v) 设 S ≥ 3,令 P = 2S。证明 (a, b, c) 是和为 P 的三元组,如果且仅如果 a, b, c 中的每一个都严格小于 S
这是一个“如果且仅如果”的证明,所以我需要在两个方向上证明它。
再次假设 a, b, c 是递增的,并且它们的和为 P。
首先,我们需要证明如果 a+b > c,那么 c < S。假设 c ≥ S。然后 a+b > c ≥ S,所以 a+b+c > 2S = P。这是一个矛盾,所以 c < S。
现在我们需要证明如果 c < S,那么 a+b > c。如果 c < S,那么 2S-c > S > c。但是 a+b+c = P = 2S,所以 a+b = 2S-c。因此 a+b > c。
(vi) 对于任何 2 ≤ a ≤ S-1,证明使得 (a, b, P-a-b) 成为一个三元组的可能值的 b 的数量为 a-1
根据第五部分,P-a-b = 2S-a-b ≤ S-1。所以 S-a+1 ≤ b。但同时 b ≤ S-1。因此,对于任何特定的 a 值,b 的值可以在 S-a+1 到 S-1 之间变化。
因此,可能的 b 的总数是 (S-1)-(S-a) = a-1。
(vii) 找到任何大于等于 6 的偶数 P 的 f(P) 的表达式
让 (a, b, P-a-b) 是和为 P 的三元组,其中 P 是偶数且不小于 6。根据第三部分和第五部分,我们知道 a 可以从 2 变到 S - 1,而根据第六部分,对于每个这样的 a 值,都有 a-1 个 b 值。
所以我们的 f(P) 的表达式可以如下推导:
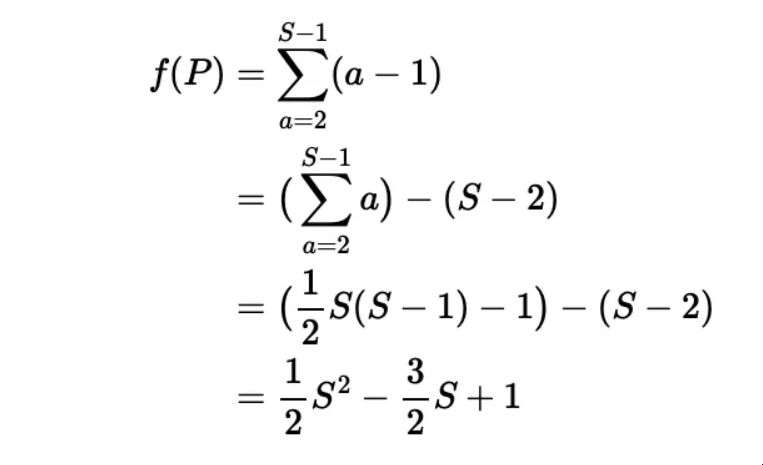
(viii) 找到 f(21)
根据第四部分,f(21) = f(24)。由于 24 是偶数且大于 6,我们可以使用第七部分的新公式,取 S = 12,得到答案是 55。
让我们使用Python 和 R 中的一个简单计数函数来双重检查:
Python
def n_triangular_triples(P):
check = []
for a in range(1, P + 1):
for b in range(1, P - a + 1):
if P - a - b > 0:
sorted_triplet = sorted([a, b, P - a - b])
if sum(sorted_triplet) == P and sorted_triplet[0] + sorted_triplet[1] > sorted_triplet[2]:
check.append(1)
return sum(check)
# 测试 P = 21
result = n_triangular_triples(21)
print(result)
R
# 简单计算和为 P 的三元组的函数
n_triangular_triples <- function(P) {
check <- c()
for (a in 1:P) {
for (b in 1:(P - a)) {
if (P - a - b > 0) {
sorted <- sort(c(a, b, P - a - b))
if ((sum(sorted) == P) && (sorted[1] + sorted[2] > sorted[3])) {
check <- append(check, 1)
}
}
}
}
sum(check)
}
# 测试 P = 21
n_triangular_triples(21)
[1] 55
当然,我们还可以使用我们的新公式来计算更大的 P 的 f(P)。
例如,f(997) = f(1000) = 124,251。
我们可以使用 Python或R 中的函数来检查,如果您愿意等待几秒钟让它遍历所有可能的三元组。
n_triangular_triples(997)
[1] 124251
GPT4 在这方面的表现如何?
并不好,尽管它渴望解释三角不等式定理,但如下所示,它的表现并不理想。我提出了三次问题,得到的答案分别是 100、22 和 190。看来真正的智能没有替代品!
您对这个问题有何看法?欢迎发表评论。
本文由 mdnice 多平台发布





![[计组03]进程详解2](https://img-blog.csdnimg.cn/52f8c8819651498ab1aa04a227530e88.png)