$${\int }_D\int (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint Pdx+Qdy$$

证明：

假设 $\int Q(x,y)dy的原函数是q(x,y),\int P(x,y)dx的原函数是p(x,y)$

并且，积分区域D如下图所示（这是最简单的形式，一般情况下积分区域的边界是x,y的函数）：

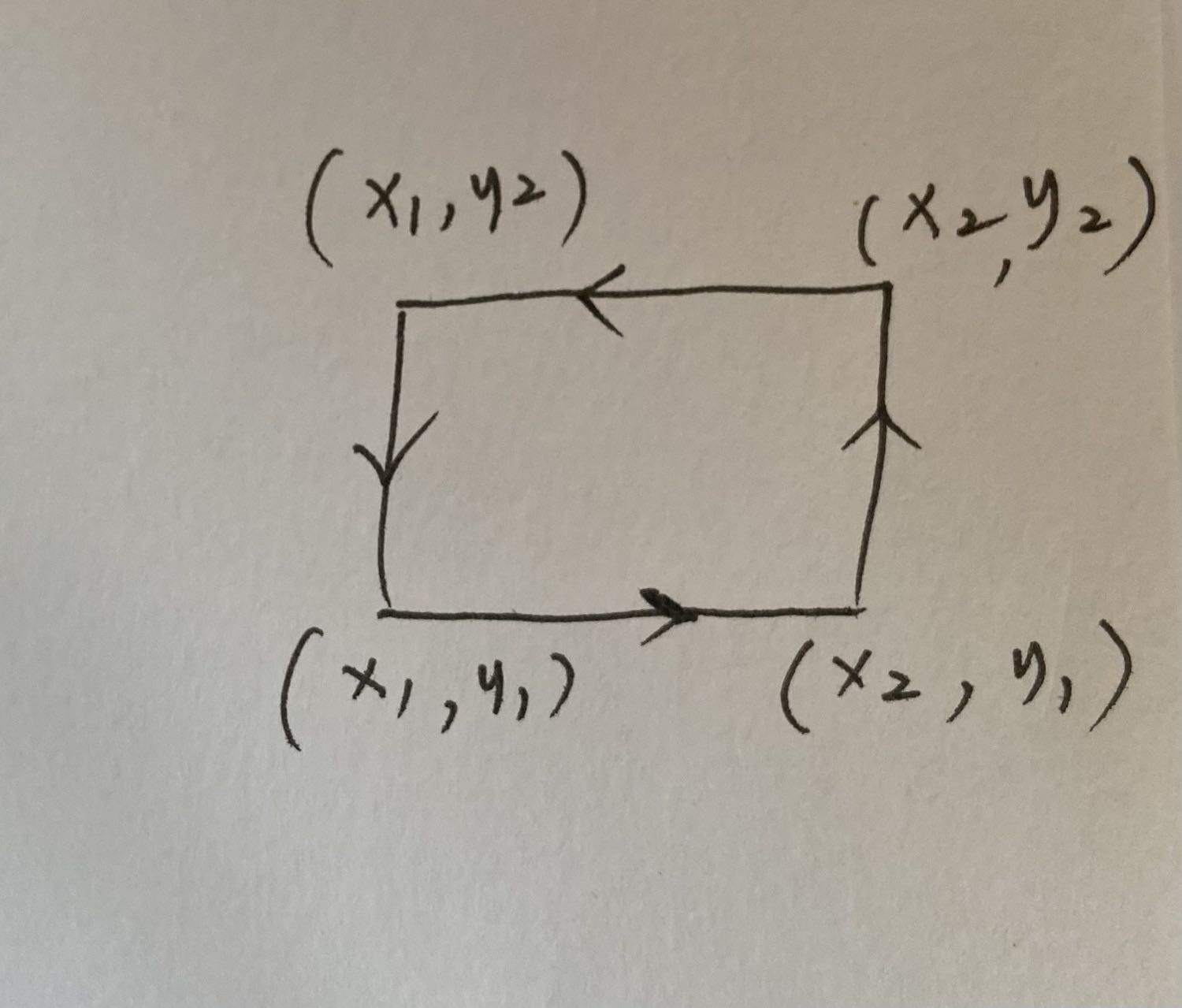
左边的积分式在积分区域运算推导如下：

$$\begin{gathered} {\int }_D\int (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy= \\ {\int }_D\int (Q_x^{\prime }-P_y^{\prime })dxdy= \\ {\int }_D\int Q_x^{\prime }dxdy-{\int }_D\int P_y^{\prime }dydx= \\ {\int }_{y_1}^{y_2}[Q(x_2,y)-Q(x_1,y)]dy-{\int }_{x_1}^{x_2}[P(x,y_2)-P(x,y_1)]dx= \\ q(x_2,y_2)-q(x_2,y_1)-q(x_1,y_2)+q(x_1,y_1) \\ -p(x_2,y_2)+p(x_1,y_2)+p(x_2,y_1)-p(x_1,y_1)\text{\hspace{1em}(1.1)} \end{gathered}$$

右边的闭区域积分推导如下：

$$\begin{gathered} \oint Pdx+Qdy= \\ {\int }_{x_2}^{x_1}P(x,y_2)dx+ \\ ({\int }_{x_1}^{x_1}P(x,y_1)dx-{\int }_{x_1}^{x_1}P(x,y_2))dx)+ \\ {\int }_{x_1}^{x_2}P(x,y_1)dx+ \\ ({\int }_{x_2}^{x_2}P(x,y_2)dx-{\int }_{x_2}^{x_2}P(x,y_1)dx)+ \\ {\int }_{y_2}^{y_1}Q(x_1,y)dy+ \\ ({\int }_{y_1}^{y_1}Q(x_2,y)dy-{\int }_{y_1}^{y_1}Q(x_1,y))dy)+ \\ {\int }_{y_1}^{y_2}Q(x_2,y)dy+ \\ ({\int }_{y_2}^{y_2}Q(x_1,y)dy-{\int }_{y_2}^{y_2}Q(x_2,y)dy)= \\ -p(x_2,y_2)+p(x_1,y_2)+p(x_2,y_1)-p(x_1,y_1)+ \\ q(x_1,y_1)-q(x_1,y_2)+q(x_2,y_2)-q(x_2,y_1)\text{\hspace{1em}(2.2)} \end{gathered}$$

从等式左右两边的计算结果可以看出，等式两边相等。

论证说明：

1. 上述闭区域的曲线积分，当从$(x_1,y_2)$到$(x_1,y_1)$对x积分时，其积分值为0。
2. 格林公式的本质是将以前的二重积分转换为曲线积分，正如同高斯公式是将三重积分转化为曲面积分，转换的前提条件是闭区域积分。
3. 需要注意的是，对y的闭区域曲线积分的符号取反，而对x的闭区域曲线积分符号不变。此种情况原因是，拿对x的闭区域积分来说，积分项的符号是如下的矩阵：$$\left|\begin{array}{cc}-1& 1\\ -1& 1\end{array}\right|$$,而对y的积分项符号矩阵为：$$\left|\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right|$$
4. 上图的示例，不仅限于第一象限，其他几个象限也满足这种规律。