哈夫曼树的构造及应用

文章目录

哈夫曼树的构造及应用
- 带权路径长度
- 哈夫曼树定义
- 哈夫曼树的性质：
- 构造哈夫曼树
- 构造哈夫曼树存储及生成算法
- 算法框架
- 代码实操:
- 应用: 哈夫曼编码

带权路径长度

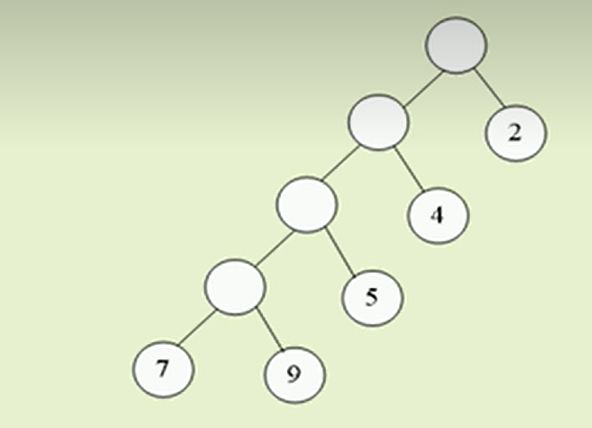
设二叉树具有n个带权值的叶子节点,那么从根节点到各个叶子节点的路径长度与相应节点权值的乘积之和,叫做二叉树的带权路径长度(WPL)。

▪ n 表示叶子结点的树木

▪ w_i 表示叶子结点k_i 的权值

▪ l_i分别表示根到k_i之间的路径长度(即从叶子节点到达根节点的分指数)。

哈夫曼树定义

▪ 具有最小带权路径长度的二叉树称为哈夫曼树，或称为最优二叉树。

哈夫曼树的性质：

n个叶子节点的二叉树,共有2n-1个节点.

证明:

设有二叉树有X个节点,则根据题意得叶子结点为n个,

由哈夫曼树的性质可得, 该树除了叶子节点的度数为零外, 其余节点度数都为2 ,所以

总度数 = (X - n) * 2 ①

并且根据总结点数 X , 和除了根节点外,其他节点都有一个前驱分支,所以

总度数 = (X - 1) ②

上面① ② 两式联立: (X - n) * 2 = (X - 1)

得, X = 2n - 1

构造哈夫曼树

▪ 策略

要使带权路径长度最小,须使权值越大的叶子节点越靠近根节点,而权值越小的叶子结点越远离根节点.

▪ 方法

(1)给定的n个权值(W₁,W₂,…W_n)构造n棵只有叶子节点的二叉树,从而得到一个二叉树的集合 F = {T₁,T₂,…,T_n};

(2)在F中选取根节点的权值最小和次小的两颗二叉树作为左、右子树，构造一棵新的二叉树，新的二叉树根节点的权值为其左、右子树根节点权值之和。

（3）在集合F中删除作为左、右子树的两颗二叉树，并将新建的二叉树加入到集合F中；

（4）重复（2）、（3）两步，当F中只剩下一颗二叉树时，这颗二叉树便是要建立的哈夫曼树。

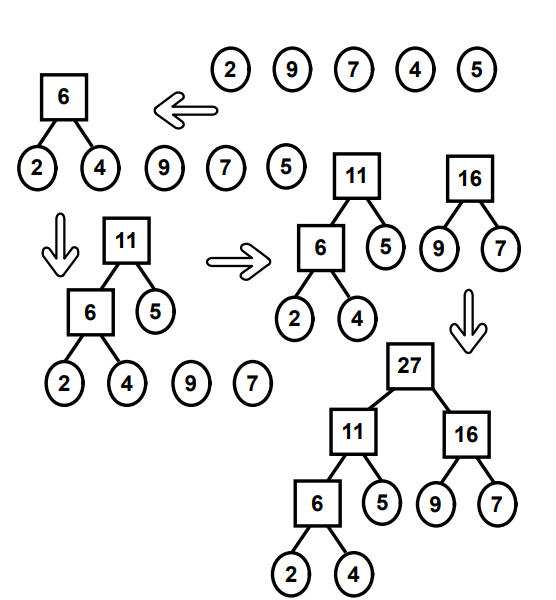
构造哈夫曼树存储及生成算法

#define N 5			//叶子节点数
typedef struct
{
    char data;		//节点值
    float weight;	//权重
    int  parent;	//双亲节点
    int  lchild;	//左孩子节点
    int  rchild;	//右孩子节点
}HTNode;
HTNode ht[2*N-1];

步骤1:初始化

n 个叶子节点只有data和weight域值,所有2n-1个节点的parent、lchild和rchild域置为初值-1.

步骤2:

开始构造,逐步选出两个最小和次小的权值节点,然后作为组合,形成哈夫曼树

重复处理每个非叶子节点ht[i] ,(ht[n] ~ ht[2n-2], i: n ~ 2n-2 )

▪ 从 ht[0] ~ h [i-1]中找出根节点(即其parent域为-1)最小的两个节点ht[lnode]和ht[rnode]

▪ ht[node]和ht[rnode]作为左右子树,增加他们的双亲节点ht[i],有: ht[i].weight = ht[node].weight + ht[rnode].weight

算法框架

//传入

代码实操:

//传入构建所用数组和 叶子节点的个数,方便后续操作
void CreateHT(HTNode ht[],int n)
{
    //定义计数器,定义节点左右孩子的序号
    int i,j,k,lnode,rnode;
    //定义权值最小和次小的数组序号
    float min1,min2;
    //所有节点的数据区初始化,包括数组中记录节点双亲、左右孩子的数据区。
    for(i=0;i<2*n-1;i++)
    {
		ht[i].parent=ht[i].lchild = ht[i].rchild = -1;
    }
    //开始构建叶子节点的双亲节点,运用哈夫曼树的思想,先挑出权值最小和次小的节点,将他们合并成新节点,剔除选中后的节点,后续接着操作
    for(i = n; i<2*n-1; i++)
    {
        //找出权重最小的两个节点
		//先把两个变量变成超过所有权值的数值
        min1 = min2 = 32145;
        //构建的新节点,刚开始左右孩子置为 -1 ,表示无
        lnode = rnode = -1;
        //开始寻找最小和次小
        //开始遍历所有节点,
        for(k=0;k<=i-1;k++)		//注意细节, k<i-1 , 只遍历构建的新节点的前面的节点
        {
            if(ht[k].parent=-1)		//挑选不为 - 1 的节点,意思就是没有被挑选的
            {
                if(ht[k].weight<min1)		//比最小的还小 , 那就给老大
                {
                    min2 = min1;			//给老大之前, 老大穿过的给老二
                    rnode = lnode;			// 左孩子是上次最小的,找到更小的了,所以现在交给右孩子 
                    min1 = ht[k].weight;		//最小的序号给老大
                    lnode = k;				// 左孩子的序号 是 k, 是最小的节点的序号
                }             
                else if(ht[k].weight<min2)		//如果老大 , 有的节点没看上, 比老大大,又比老二小, 那我们老二不能放过了
                {
                    min2 = ht[k].weight;		//序号安排
                    rnode = k;				// 仍然是变成右孩子,因为是次小的
                }                    
            }                
        }                    
        //生成一个双亲节点
        ht[lnode].parent = i;		//现在生成最小和次小的双亲 , 左孩子的父母,右孩子的父母
        ht[rnode].parent = i;
        ht[i].weight = ht[lnode].weight + ht[rnode].weight;	//新节点的权重为两个孩子的和
        ht[i].lchild = lnode;			// 标记左右孩子
        ht[i].rchild = rnode;
    }            
}