感知机是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值
感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型
一.模型介绍和学习策略
1.模型介绍

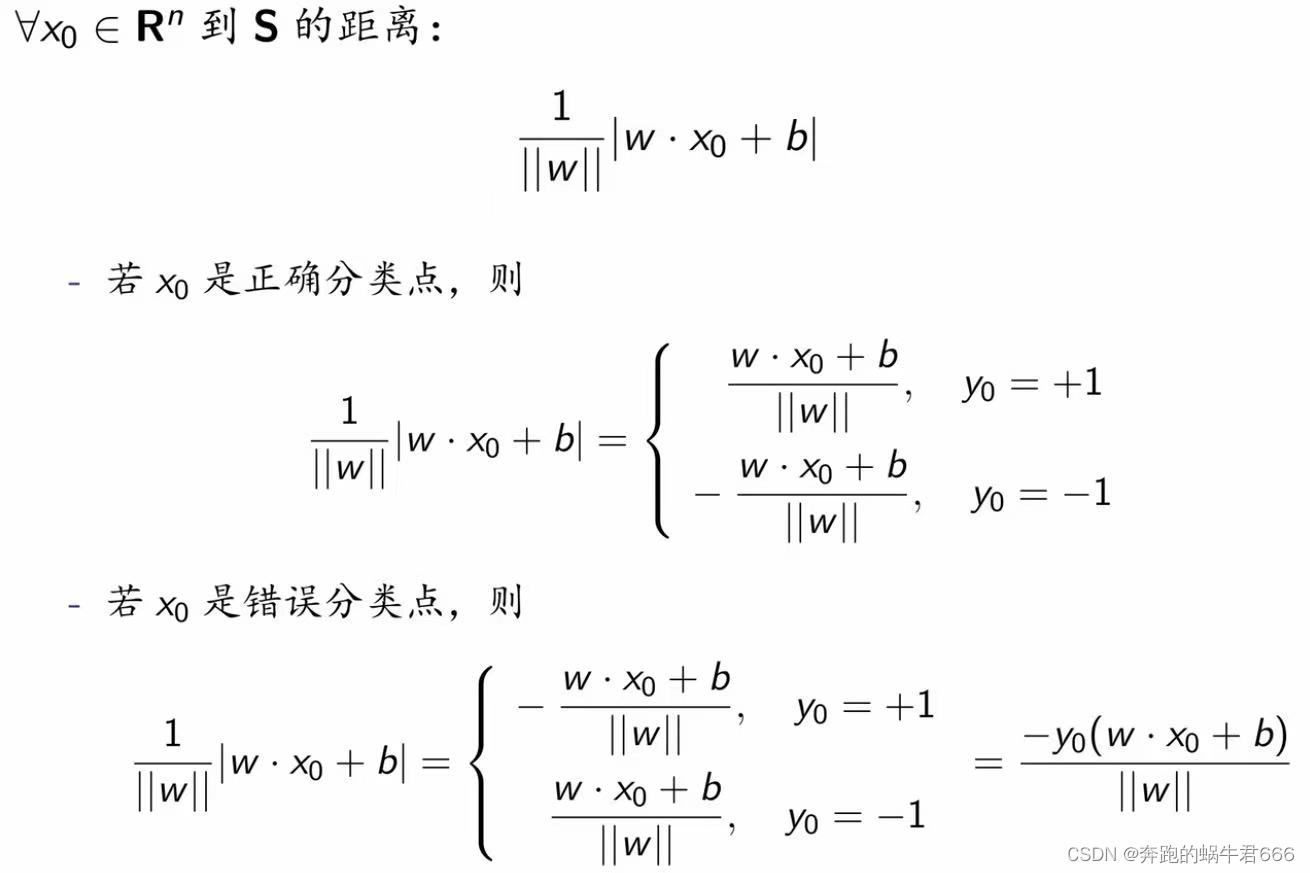
2.几何含义

3.学习策略
数据集的线性可分性

 二.梯度下降法
二.梯度下降法
1.概念

2.算法

3.原理
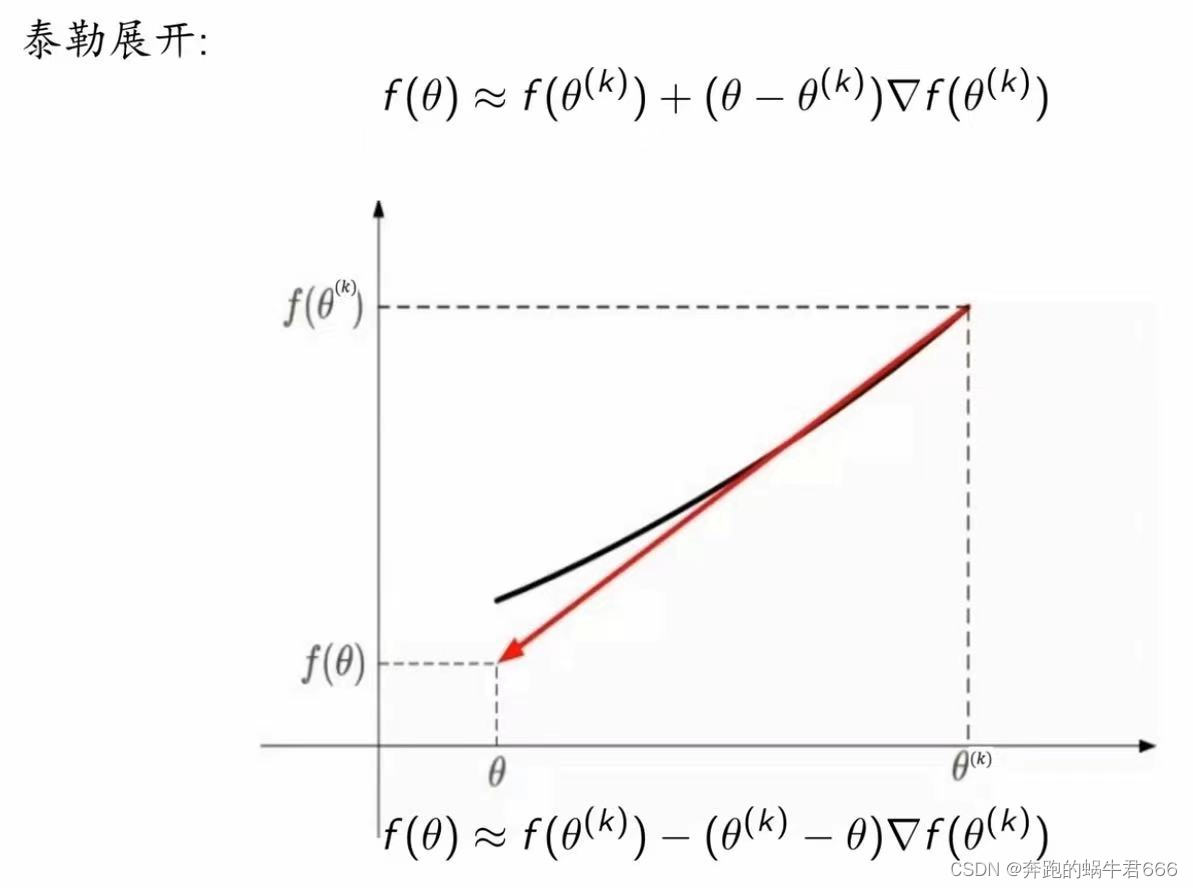

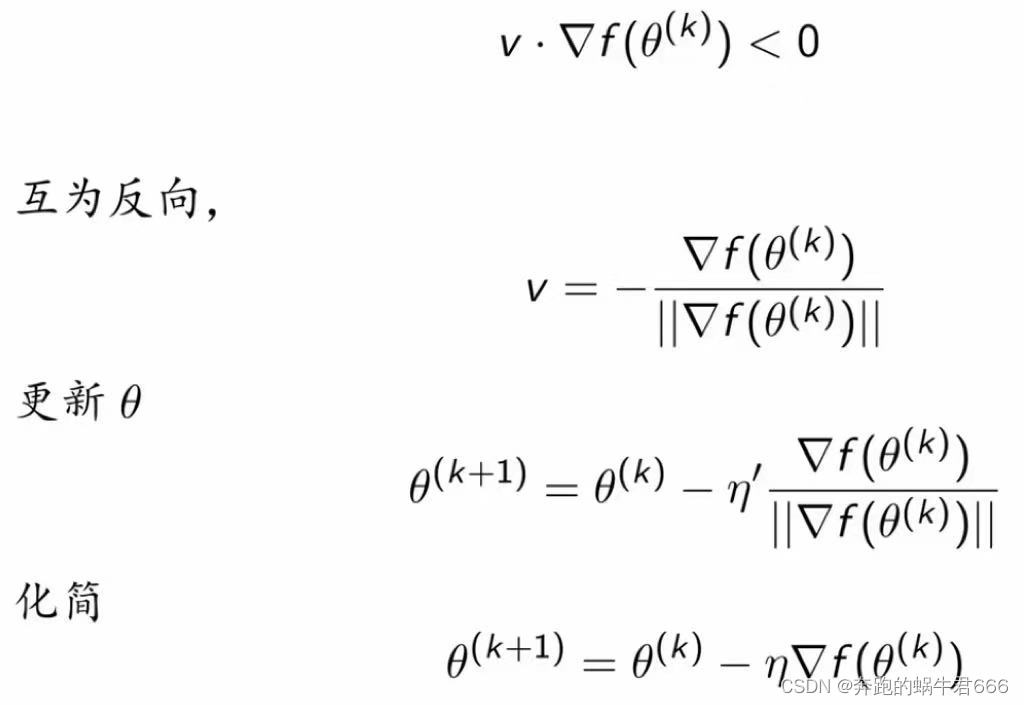
三.原始形式
首先任意选取一个超平面,然后用梯度下降法不断极小化目标函数
在这个过程中一次随机选取一个误分类点使其梯度下降
1.学习问题
 2.原始形式:随机梯度下降法
2.原始形式:随机梯度下降法


四.对偶形式


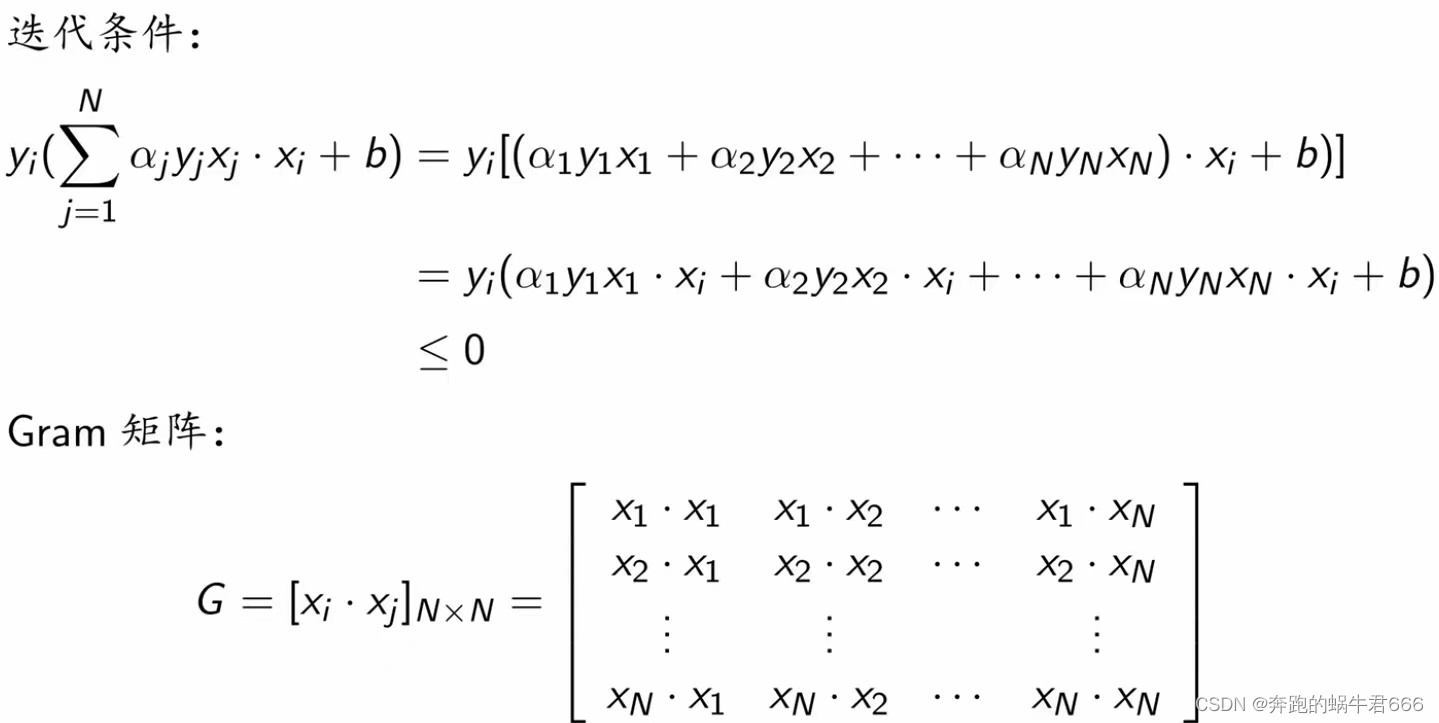
五.算法的收敛性
对于线性可分数据集感知机学习算法原始形式收敛,即经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型
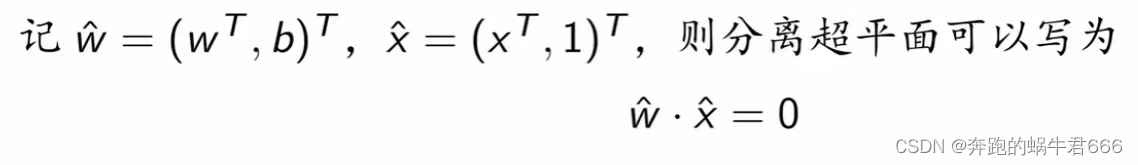

证明
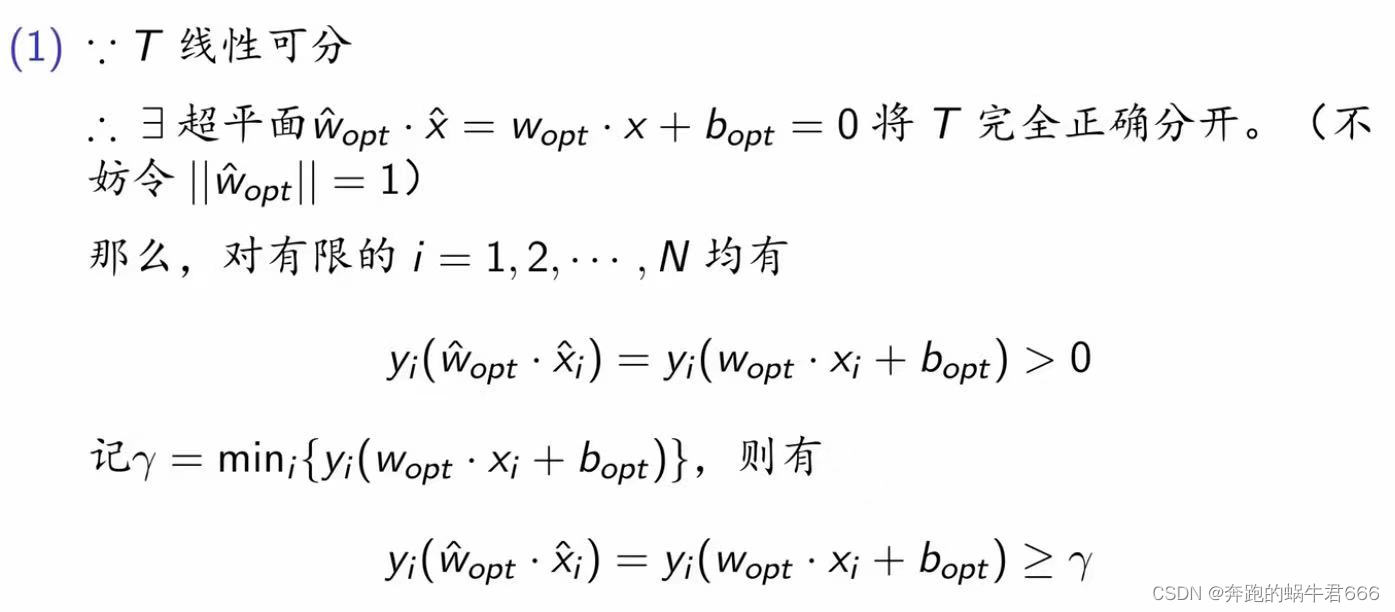



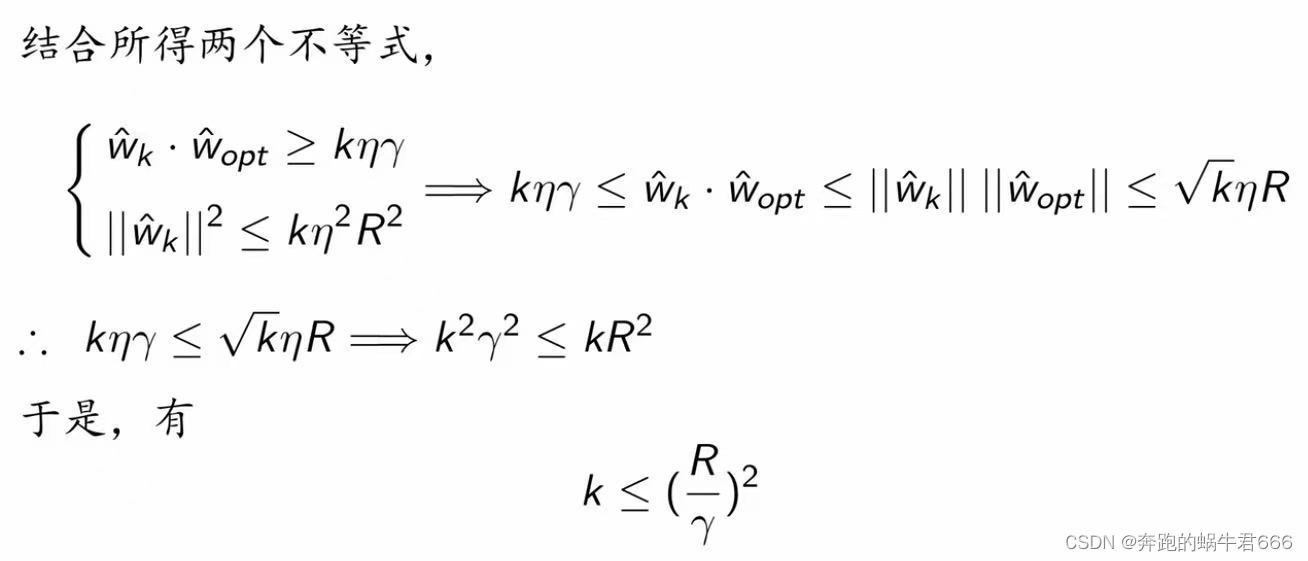 收敛性:对于线性可分的T,经过有限次搜索,可得将T完全正确分开的分离超平面
收敛性:对于线性可分的T,经过有限次搜索,可得将T完全正确分开的分离超平面
依赖性:不同的初值选择,或者迭代过程中不同的误分类点选择顺序,可能会得到不同的分离超平面
对于线性不可分的T,算法不收敛,迭代结果会发生震荡
为得到唯一分离超平面,需增加约束条件
六.Python实现
随即梯度下降法 Stochastic Gradient Descent
随机抽取一个误分类点使其梯度下降。
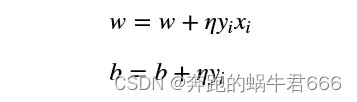
当实例点被误分类,即位于分离超平面的错误侧,则调整w,b的值,使分离超平面向该无分类点的一侧移动,直至误分类点被正确分类
# 数据线性可分,二分类数据
# 此处为一元一次线性方程
class Model:
def __init__(self):
self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
self.b = 0
self.l_rate = 0.1
# self.data = data
def sign(self, x, w, b):
y = np.dot(x, w) + b
return y
# 随机梯度下降法
def fit(self, X_train, y_train):
is_wrong = False
while not is_wrong:
wrong_count = 0
for d in range(len(X_train)):
X = X_train[d]
y = y_train[d]
if y * self.sign(X, self.w, self.b) <= 0:
self.w = self.w + self.l_rate * np.dot(y, X)
self.b = self.b + self.l_rate * y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return 'Perceptron Model!'
def score(self):
pass
perceptron = Model()
perceptron.fit(X, y)
x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()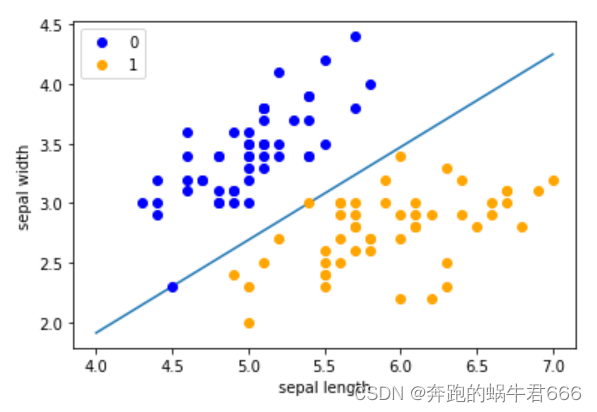

![[附源码]计算机毕业设计Python的个人理财系统(程序+源码+LW文档)](https://img-blog.csdnimg.cn/4e0dd35874b24a818a88841213b0540d.png)