-----------------------往期目录------------------
1、灰狼优化算法
文章目录
- 天鹰优化器
- 一、第一种搜索方法
- 二、第二种搜素方法
- 三、第三种搜素方法
- 四、第四种搜索方法
- 代码实现
天鹰优化器
Aquila Optimizer(AO),灵感来自Aquila在捕捉猎物过程中的自然界行为。因此,所提出的AO算法的优化过程分为四种方法:用垂直弯腰的高腾空选择搜索空间,用轮廓飞行和短滑翔攻击在发散搜索空间内探索,用低飞行和慢下降攻击在收敛搜索空间内利用,以及用步行和抓取猎物俯冲。为了验证新的优化器为不同优化问题找到最优解的能力,进行了一系列实验。
提示:以下是本篇文章正文内容,下面案例可供参考
一、第一种搜索方法
Aquila识别猎物区域,并通过垂直弯腰的高飞选择最佳狩猎区域。在这里,天鹰从高飞广泛探索者来确定170°搜索空间的区域,猎物在哪里。图1显示了Aquila高飞垂直弯腰的行为。这种行为在数学上表现为下列等式。
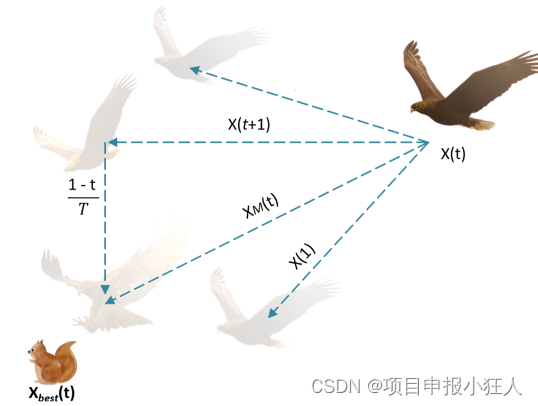
图1:Aquila高飞垂直弯腰的行为
X
1
(
t
+
1
)
=
X
b
e
s
t
(
t
)
×
(
1
−
t
T
)
+
(
X
M
(
t
)
−
X
b
e
s
t
(
t
)
∗
r
a
n
d
)
X_{1}(t+1)=X_{b e s t}(t)\times\left(1-{\frac{t}{T}}\right)+(X_{M}(t)-X_{b e s t}(t)*r a n d)
X1(t+1)=Xbest(t)×(1−Tt)+(XM(t)−Xbest(t)∗rand)
X
M
(
t
)
=
1
N
∑
i
=
1
N
X
i
(
t
)
,
∀
j
=
1
,
2
,
.
.
.
,
D
i
m
X_{M}(t)={\frac{1}{N}}\sum_{i=1}^{N}X_{i}(t),\forall j=1,2,...,D i m
XM(t)=N1i=1∑NXi(t),∀j=1,2,...,Dim
其中,
X
1
(
t
+
1
)
X_{1}(t+1)
X1(t+1)是t的下一次迭代的解,由第一种搜索方法(
X
1
X_{1}
X1)生成。
X
b
e
s
t
(
t
)
X_{b e s t}(t)
Xbest(t)是直到第t次迭代的最佳获得解,这反映了猎物的近似位置。这个方程
1
−
t
T
1-{\frac{t}{T}}
1−Tt用于控制通过迭代的扩展搜索(探索)。
X
M
(
t
)
X_M(t)
XM(t)表示在第t次迭代时连接的当前解的位置平均值,
r
a
n
d
∈
[
0
,
1
]
rand∈[0,1]
rand∈[0,1].
二、第二种搜素方法
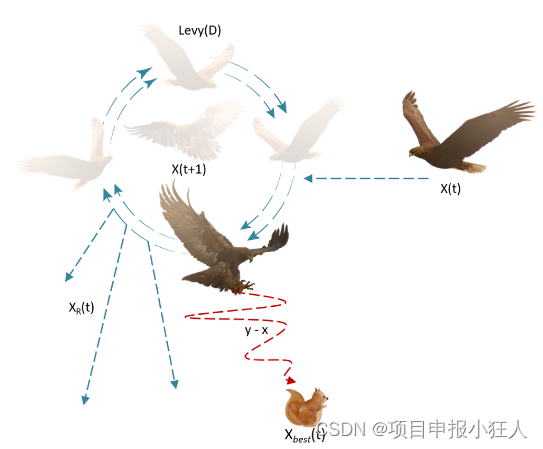
X
2
(
t
+
1
)
=
X
b
e
s
t
(
t
)
×
L
e
v
y
(
D
)
+
X
R
(
t
)
+
(
y
−
x
)
∗
r
a
n
d
,
X_{2}(t+1)=X_{b e s t}(t)\times L e v y(D)+X_{R}(t)+(y-x)*r a n d,
X2(t+1)=Xbest(t)×Levy(D)+XR(t)+(y−x)∗rand,
其中
X
2
(
t
+
1
)
X_2(t+1)
X2(t+1)是
t
t
t 的下一次迭代的解,由第二种搜索方法
X
2
X_2
X2生成,
D
D
D是维数空间,
L
e
v
y
(
D
)
Levy(D)
Levy(D)是
l
e
v
y
levy
levy飞行分布函数,使用公式计算,
X
R
(
t
)
X_R(t)
XR(t)是第
t
t
t 次迭代时在
[
1
,
N
]
[1,N]
[1,N]范围内取的随机解.
L
e
v
y
(
D
)
=
s
×
u
×
σ
∣
v
∣
1
β
L e v y(D)=s\times{\frac{u\times\sigma}{|v|^{\frac{1}{β}}}}
Levy(D)=s×∣v∣β1u×σ
其中s是固定为0.01的常量值,
u
u
u和
v
v
v 是
0
0
0到1之间的随机数,
σ
σ
σ 使用下列等式计算:
σ
=
Γ
(
1
+
β
)
×
sin
(
π
β
2
)
Γ
(
1
+
β
2
)
×
β
×
2
β
−
1
2
\sigma={\frac{\Gamma(1+\beta)\times\sin\left({\frac{\pi\beta}{2}}\right)}{\Gamma\left({\frac{1+\beta}{2}}\right)\times\beta\times2^{\frac{\beta-1}{2}}}}
σ=Γ(21+β)×β×22β−1Γ(1+β)×sin(2πβ)
其中β是固定为1.5的常数值.
r
=
r
1
+
U
×
D
1
θ
=
−
ω
×
D
1
+
θ
1
θ
1
=
3
×
π
2
\begin{array}{c}{{r=r_{1}+U\times D_{1}}}\\ {{}}\\ {{\theta=-\omega\times D_{1}+\theta_{1}}}\\ {{}}\\ {{\theta_{1}=\frac{3\times\pi}{2}}}\end{array}
r=r1+U×D1θ=−ω×D1+θ1θ1=23×π
R
1
∈
[
1
,
20
]
R_1∈[1,20]
R1∈[1,20],用于固定搜索周期数,
U
U
U是一个固定为0.00565的小值。
D
1
D_1
D1是从1到搜索空间长度(Dim)的整数,
ω
\omega
ω是一个固定为0.005的小值。以螺旋形状显示了AO的行为
x
=
r
×
s
i
n
(
θ
)
y
=
r
×
cos
(
θ
)
r
=
−
0.005
×
D
1
+
3
×
π
2
\begin{array}{c}{{x=r\times s\mathrm{in}(\theta)}}\\ {{y=r\times\cos(\theta)}}\\ {{r=-0.005\times D_{1}+\frac{3\times\pi}{2}}}\end{array}
x=r×sin(θ)y=r×cos(θ)r=−0.005×D1+23×π
三、第三种搜素方法
在第三种方法(X3)中,当准确指定猎物区域,并且天鹰准备着陆和攻击时,天鹰垂直下降,进行初步攻击以发现猎物反应。
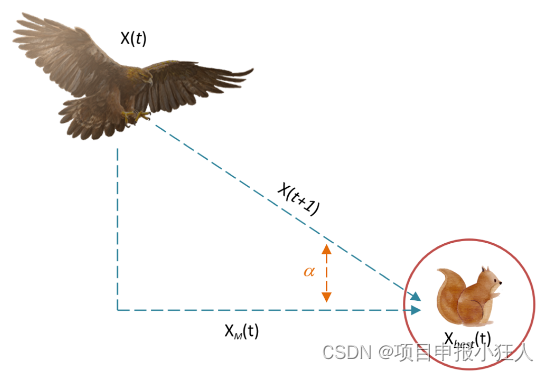
称为慢速下降攻击的低空飞行。在这里,AO利用目标的选定区域接近猎物并进行攻击。图显示了Aquila低空飞行慢速下降攻击的行为
X
3
(
t
+
1
)
=
(
X
b
e
s
t
(
t
)
−
X
M
(
t
)
)
×
α
−
r
a
n
d
+
(
(
U
B
−
L
B
)
×
r
a
n
d
+
L
B
)
×
δ
X_{3}(t+1)=(X_{b e s t}(t)-X_{M}(t))\times\alpha-r a n d+((U B-L B)\times r a n d+L B)\times\delta
X3(t+1)=(Xbest(t)−XM(t))×α−rand+((UB−LB)×rand+LB)×δ
X
3
(
t
+
1
)
X_3(t+1)
X3(t+1)是由第三种搜索方法
X
3
X_3
X3生成的t的下一次迭代的解。
X
B
e
s
t
(
t
)
X_Best(t)
XBest(t)是指第i次迭代前猎物的近似位置(最佳获得的解),
X
M
(
t
)
X_M(t)
XM(t)是第t次迭代时当前解的平均值,使用等式计算。rand是0到1之间的随机值。
α
\alpha
α和
δ
\delta
δ是本文固定为小值(0.1)的开发调整参数。
L
B
L_B
LB表示给定问题的下界,
U
B
U_B
UB表示200的上界.
四、第四种搜索方法
接近猎物时,Aquila根据猎物的随机运动在陆地上攻击猎物。这种方法称为步行并抓住猎物。这里,最后,AO在最后一个位置攻击猎物。图显示了Aquila步行并抓住猎物的行为。
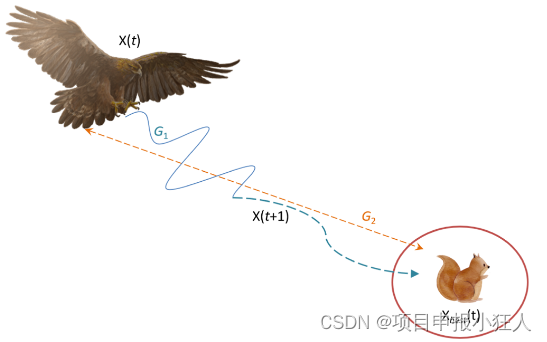
X
4
(
t
+
1
)
=
Q
F
×
X
b
e
x
(
t
)
−
(
G
1
×
X
(
t
)
×
r
a
n
d
)
−
G
2
×
L
e
ν
y
(
D
)
+
r
a
n
d
×
G
1
\begin{array}{c}{{X_{4}(t+1)=Q F\times X_{b e x}(t)-(G_{1}\times X(t)\times r a n d)-G_{2}\times L e\nu y(D)+r a n d×G_1}}\\{{}}\end{array}
X4(t+1)=QF×Xbex(t)−(G1×X(t)×rand)−G2×Leνy(D)+rand×G1
Q
F
(
t
)
=
t
r
a
n
d
−
1
(
1
−
T
)
2
Q F(t)=t^{\frac{rand-1}{(1-T)^{2}}}
QF(t)=t(1−T)2rand−1
G
1
=
2
×
r
a
n
d
−
1
G
2
=
2
×
(
1
−
t
T
)
\begin{array}{c}{{G_{1}=2\times r a n d-1}}\\ {{}}\\ {{G_{2}=2\times\left(1-\frac{t}{T}\right)}}\end{array}
G1=2×rand−1G2=2×(1−Tt)
Q
F
(
t
)
QF(t)
QF(t)是第
i
t
h
i^{th}
ith次迭代时的质量函数值,
r
a
n
d
rand
rand是0到1之间的随机值。t和T分别表示当前迭代和最大迭代次数。
L
e
v
y
(
D
)
Levy(D)
Levy(D)是使用方程计算的
l
e
v
y
levy
levy飞行分布函数
代码实现
完整代码请私信领取:
function [Best_FF,Best_P,conv]=AO(N,T,LB,UB,Dim,F_obj)
Best_P=zeros(1,Dim);
Best_FF=inf;
X=initialization(N,Dim,UB,LB);
Xnew=X;
Ffun=zeros(1,size(X,1));
Ffun_new=zeros(1,size(Xnew,1));
t=1;
alpha=0.1;
delta=0.1;
while t<T+1
for i=1:size(X,1)
F_UB=X(i,:)>UB;
F_LB=X(i,:)<LB;
X(i,:)=(X(i,:).*(~(F_UB+F_LB)))+UB.*F_UB+LB.*F_LB;
Ffun(1,i)=F_obj(X(i,:));
if Ffun(1,i)<Best_FF
Best_FF=Ffun(1,i);
Best_P=X(i,:);
end
end
G2=2*rand()-1; % Eq. (16)
G1=2*(1-(t/T)); % Eq. (17)
to = 1:Dim;
u = .0265;
r0 = 10;
r = r0 +u*to;
omega = .005;
phi0 = 3*pi/2;
phi = -omega*to+phi0;
x = r .* sin(phi); % Eq. (9)
y = r .* cos(phi); % Eq. (10)
QF=t^((2*rand()-1)/(1-T)^2); % Eq. (15)
%-------------------------------------------------------------------------------------
for i=1:size(X,1)
%-------------------------------------------------------------------------------------
if t<=(2/3)*T
if rand <0.5
Xnew(i,:)=Best_P(1,:)*(1-t/T)+(mean(X(i,:))-Best_P(1,:))*rand(); % Eq. (3) and Eq. (4)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
else
%-------------------------------------------------------------------------------------
Xnew(i,:)=Best_P(1,:).*Levy(Dim)+X((floor(N*rand()+1)),:)+(y-x)*rand; % Eq. (5)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
end
%-------------------------------------------------------------------------------------
else
if rand<0.5
Xnew(i,:)=(Best_P(1,:)-mean(X))*alpha-rand+((UB-LB)*rand+LB)*delta; % Eq. (13)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
else
%-------------------------------------------------------------------------------------
Xnew(i,:)=QF*Best_P(1,:)-(G2*X(i,:)*rand)-G1.*Levy(Dim)+rand*G2; % Eq. (14)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
end
end
end
%-------------------------------------------------------------------------------------
if mod(t,100)==0
display(['At iteration ', num2str(t), ' the best solution fitness is ', num2str(Best_FF)]);
end
conv(t)=Best_FF;
t=t+1;
end
end
function o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;
end
Abualigah, L., Yousri, D., Elaziz, M.A., Ewees, A.A., A. Al-qaness, M.A., Gandomi, A.H., Aquila Optimizer: A novel meta-heuristic optimization Algorithm, Computers & Industrial Engineering (2021), doi: https://doi.org/10.1016/j.cie.2021.107250





![[vue问题]开发中问题集合](https://img-blog.csdnimg.cn/5f73875ba75d400798ca525aa86ffd34.png)