安装PyTorch Geometric

安装工具包

打开链接https://github.com/pyg-team/pytorch_geometric，点击图中箭头处，使用编译好的版本来安装:

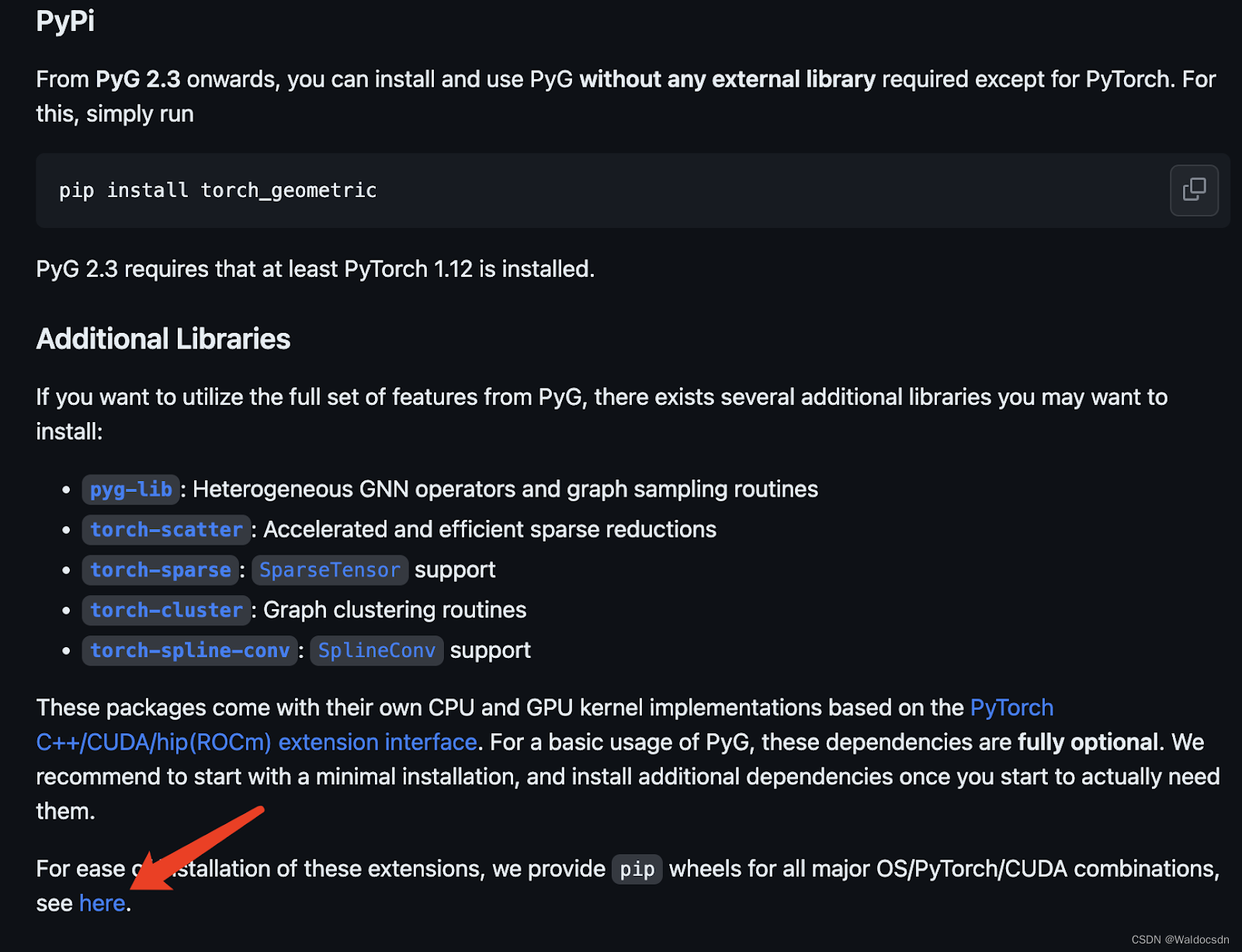
使用以下代码片段来查看PyTorch、CUDA和Python的版本：

import torch

# 查看PyTorch版本
print("PyTorch版本:", torch.__version__)

# 查看CUDA版本（如果使用GPU）
if torch.cuda.is_available():
    print("CUDA版本:", torch.version.cuda)
else:
    print("未找到可用的CUDA")

# 查看Python版本
import sys
print("Python版本:", sys.version)

运行截图：

根据版本点击下图中链接:

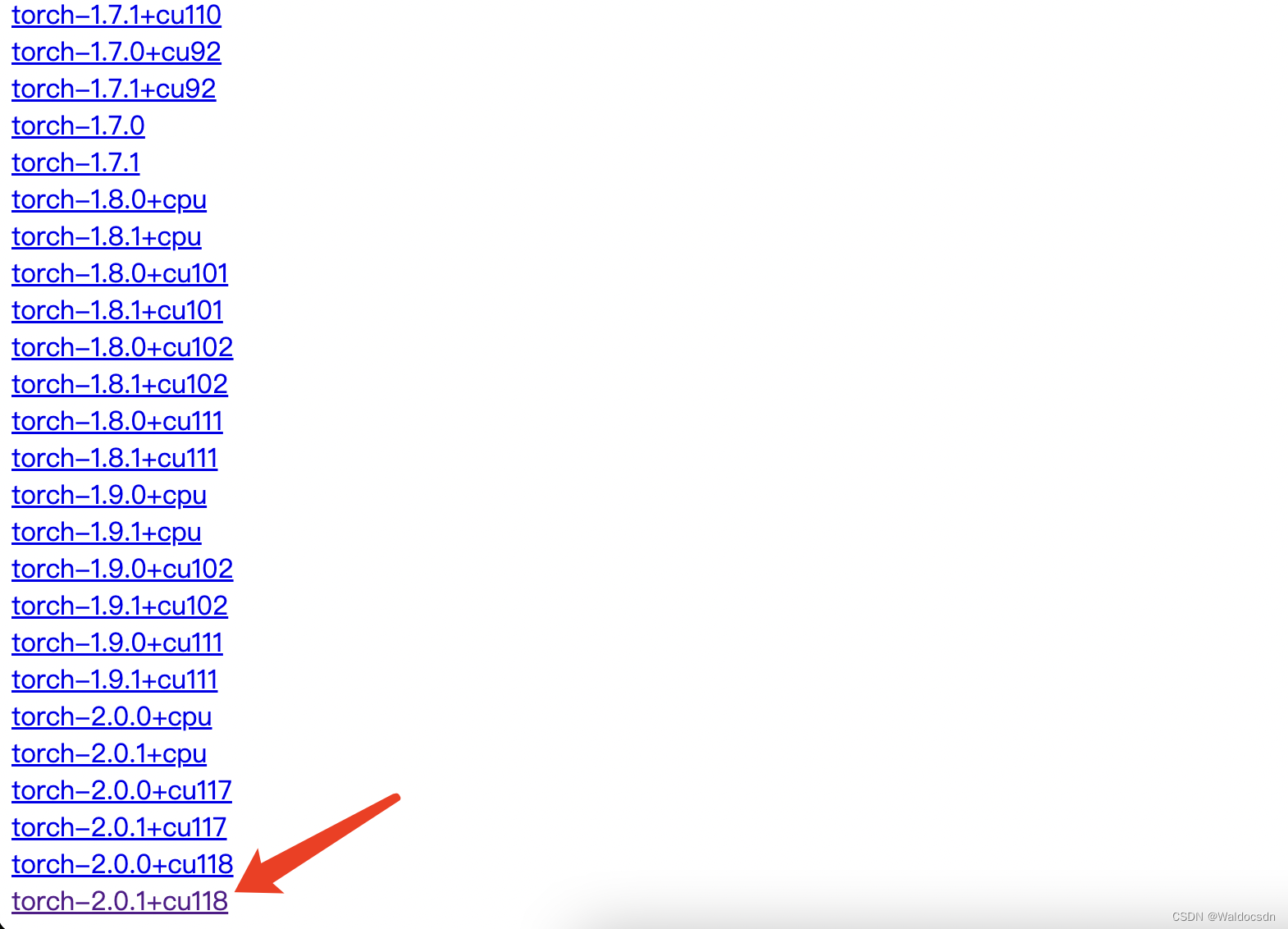
再根据python版本选择安装相应的依赖包，安装命令pip install 包名:

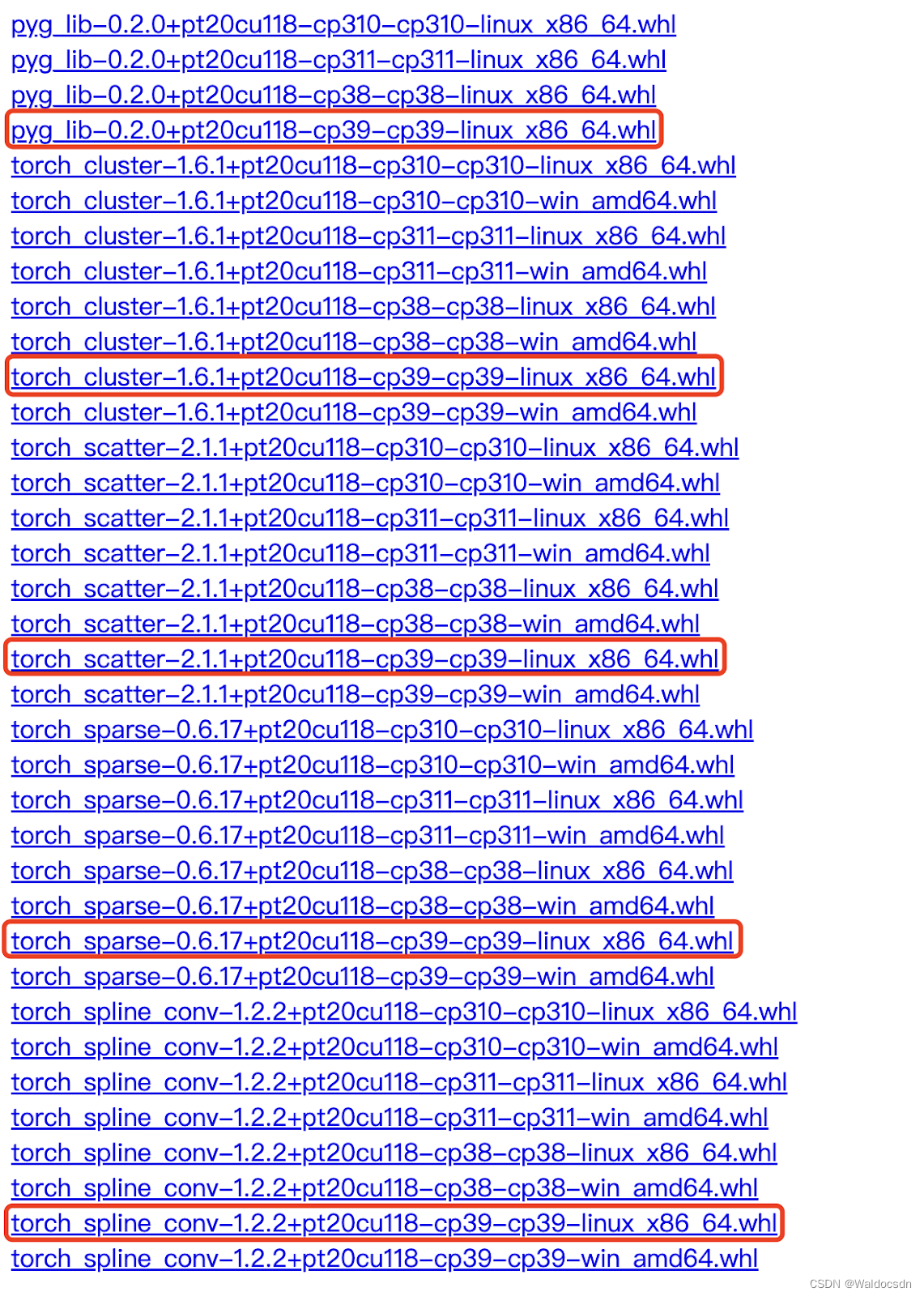
最后执行命令pip install torch_geometric便可

在KarateClub数据集上使用图卷积网络 (GCN) 进行节点分类

本部分为代码学习，可以将代码放入Jupyter中运行

两个画图函数

%matplotlib inline
import torch
import networkx as nx
import matplotlib.pyplot as plt


def visualize_graph(G, color):
    plt.figure(figsize=(7,7))
    plt.xticks([])
    plt.yticks([])
    nx.draw_networkx(G, pos=nx.spring_layout(G, seed=42), with_labels=False,
                     node_color=color, cmap="Set2")
    plt.show()


def visualize_embedding(h, color, epoch=None, loss=None):
    plt.figure(figsize=(7,7))
    plt.xticks([])
    plt.yticks([])
    h = h.detach().cpu().numpy()
    plt.scatter(h[:, 0], h[:, 1], s=140, c=color, cmap="Set2")
    if epoch is not None and loss is not None:
        plt.xlabel(f'Epoch: {epoch}, Loss: {loss.item():.4f}', fontsize=16)
    plt.show()

解析上面代码:

该代码主要包括两部分功能：使用 networkx 和 matplotlib 来可视化图结构（G）和嵌入向量（h）。

首先，我们逐行解析代码：

1. %matplotlib inline: Jupyter Notebook 的魔术命令，它可以确保在 notebook 内部显示绘制的图形。

2. 导入所需的库：

   • torch: 一个开源的深度学习库。
   • networkx as nx: 一个用于创建、操作和研究复杂网络结构和动态的 Python 库。
   • matplotlib.pyplot as plt: 用于绘图的库。

3. visualize_graph(G, color) 函数：

   • 作用：可视化图 G。
   • 参数：
     • G: 要可视化的图。
     • color: 图中节点的颜色。
   • 代码解析：
     • 设置图形大小为 7x7。
     • 删除 x, y 轴的标签。
     • 使用 nx.draw_networkx 来绘制图。其中 nx.spring_layout 是一种布局策略，它会模拟节点之间的弹簧效果，使得布局看起来更为平衡。
     • 显示图形。

4. visualize_embedding(h, color, epoch=None, loss=None) 函数：

   • 作用：可视化嵌入向量 h。
   • 参数：
     • h: 要可视化的嵌入向量。
     • color: 向量的颜色。
     • epoch (可选): 当前的训练迭代次数。
     • loss (可选): 当前的损失值。
   • 代码解析：
     • 设置图形大小为 7x7。
     • 删除 x, y 轴的标签。
     • 将嵌入从 GPU 转移到 CPU，并从 PyTorch 张量转换为 numpy 数组。
     • 使用 plt.scatter 函数在二维空间中绘制每个嵌入。
     • 如果提供了 epoch 和 loss，则在图形的 x 轴标签上显示这些值。
     • 显示图形。

简而言之，这段代码提供了两个函数，一个用于可视化图结构，另一个用于可视化嵌入。这在图神经网络的背景下尤为有用，例如当需要查看节点嵌入的演化或与原始图结构进行比较时。

Graph Neural Networks

• 致力于解决不规则数据结构（图像和文本相对格式都固定，但是社交网络与化学分子等格式肯定不是固定的）
• GNN模型迭代更新主要基于图中每个节点及其邻居的信息，基本表示如下：

$${\mathbf{x}}_v^{(\ell +1)}=f_{\theta }^{(\ell +1)}\left({\mathbf{x}}_v^{(\ell )},\left\{{\mathbf{x}}_w^{(\ell )}:w\in \mathcal{N}(v)\right\}\right)$$

节点的特征： ${\mathbf{x}}_v^{(\ell )}$ ， $v\in \mathcal{V}$ 在图中 $\mathcal{G}=(\mathcal{V},\mathcal{E})$ 根据其邻居信息进行更新 $\mathcal{N}(v)$:

数据集：Zachary’s karate club network.

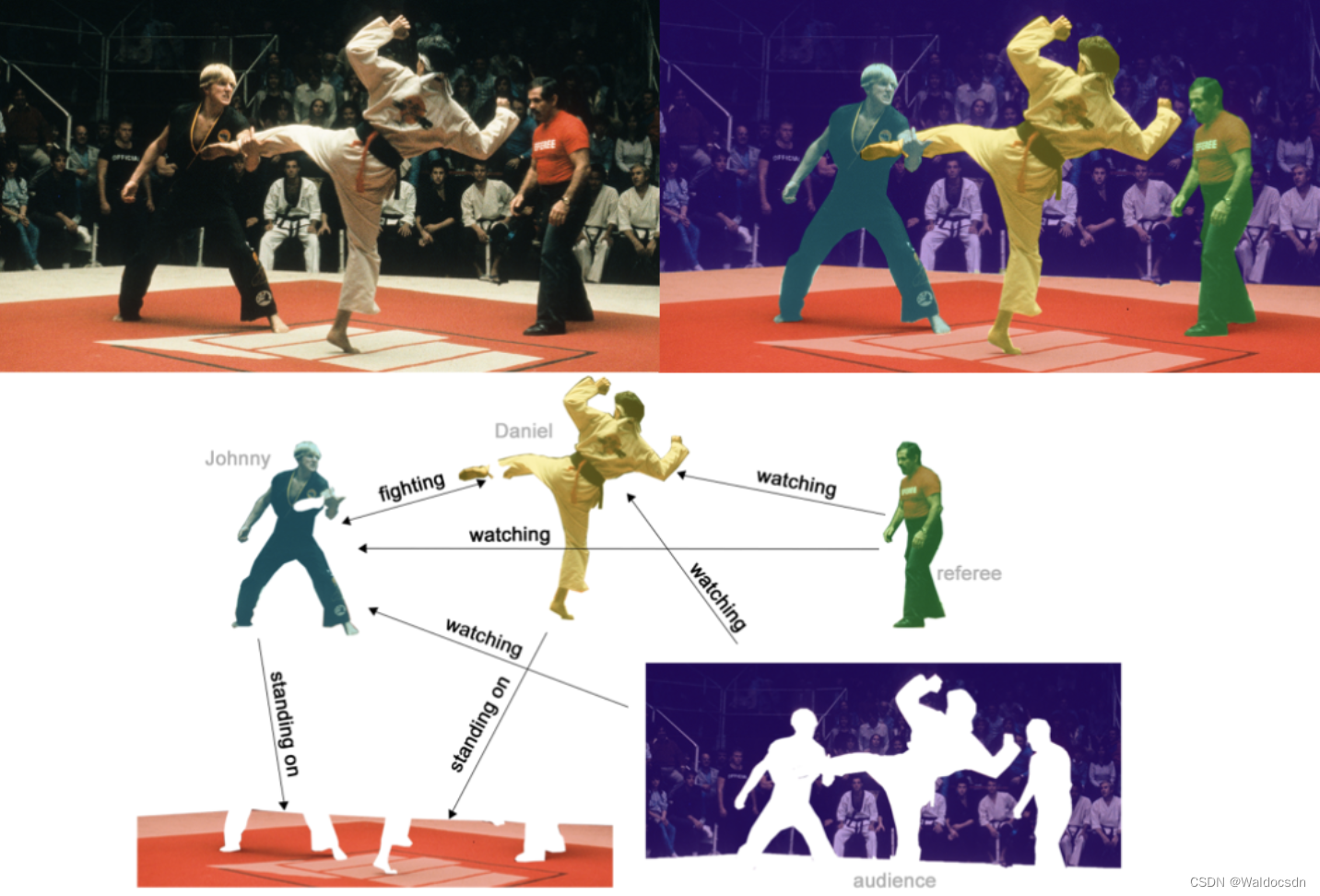
该图描述了一个空手道俱乐部会员的社交关系，以34名会员作为节点，如果两位会员在俱乐部之外仍保持社交关系，则在节点间增加一条边。
每个节点具有一个34维的特征向量，一共有78条边。
在收集数据的过程中，管理人员 John A 和 教练 Mr. Hi（化名）之间产生了冲突，会员们选择了站队，一半会员跟随 Mr. Hi 成立了新俱乐部，剩下一半会员找了新教练或退出了俱乐部。

PyTorch Geometric

• 这个就是咱们的核心了，说白了就是这里实现了各种图神经网络中的方法
• 咱们直接调用就可以了：PyTorch Geometric (PyG) library

数据集介绍

• 可以直接参考其API：https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html#torch_geometric.datasets.KarateClub

from torch_geometric.datasets import KarateClub

dataset = KarateClub()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

data = dataset[0]  # Get the first graph object.
print(data)

输出为:

Dataset: KarateClub():
======================
Number of graphs: 1
Number of features: 34
Number of classes: 4

Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])

解析上面代码:
此代码使用 torch_geometric.datasets 中的 KarateClub 数据集，这是一个经常在图神经网络研究中使用的经典数据集。KarateClub 数据集描述了一个学校空手道俱乐部的成员之间的关系，其中成员分为两个派系。

接下来，我们逐步解析代码：

1. 导入数据集:

   from torch_geometric.datasets import KarateClub
   

2. 加载数据集:

   dataset = KarateClub()
   

   这会实例化 KarateClub 数据集，并下载相关数据（如果还没有的话）。

3. 打印数据集的一般信息:

   • print(f'Dataset: {dataset}:'): 打印数据集的描述。
   • print(f'Number of graphs: {len(dataset)}'): 打印数据集中图的数量。输出显示只有一个图。
   • print(f'Number of features: {dataset.num_features}'): 打印每个节点的特征数量。输出显示每个节点有 34 个特征。
   • print(f'Number of classes: {dataset.num_classes}'): 打印数据集中的类别数量。输出显示有 4 个类别（四分类任务）。

4. 获取第一个图对象:

   data = dataset[0]
   

   这会获取数据集中的第一个（也是唯一的）图对象。torch_geometric 中的图数据通常用 Data 对象表示，它包含节点、边以及其他相关信息。

5. 打印图对象的描述:

   print(data)
   

   输出为 Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])。我们可以从中得知：

   • x=[34, 34]: 表示图中有 34 个节点，每个节点有 34 个特征。

   • edge_index=[2, 156]: 描述图的边。它是一个 2x156 的整数张量，其中每列表示一条从源节点到目标节点的边。156 表示图中有 156 条边。

   • y=[34]: 是一个长为 34 的整数张量，表示每个节点的标签。

   • train_mask=[34]: 是一个布尔张量，长度为 34，用于指示哪些节点应该用于训练。这在半监督学习设置中很常见，其中只有一小部分节点的标签是已知的。

     当我们在图数据中进行学习时，尤其是在半监督学习的情境中，我们可能只有图中部分节点的标签。半监督学习是指我们只有一小部分的数据是带标签的，而大部分数据是不带标签的，目标是使用这少量的标签数据同时学习整个数据的表示。

     在图神经网络的上下文中，我们可能只有图中的某些节点是有标签的。因此，为了在训练过程中只考虑这些有标签的节点，我们需要一个方法来区分哪些节点是用于训练的，哪些节点不是。这就是train_mask的作用。

     train_mask是一个布尔张量，长度与图中的节点数量相同。如果train_mask中的某个值为True，则表示该位置的节点是用于训练的（即该节点有标签）；如果值为False，则表示该节点不用于训练。

     例如，假设我们有以下train_mask：

     train_mask = [True, True, False, False, True]
     

     这意味着图中的第一个、第二个和第五个节点有标签，将被用于训练；而第三个和第四个节点没有标签，不会被用于训练。

     在图神经网络的训练过程中，我们只会计算并反向传播那些train_mask值为True的节点的损失，从而使模型能够利用这些已知的标签信息。

总的来说，这段代码简单地加载了 KarateClub 数据集并显示了其基本信息。这个数据集是描述一个空手道俱乐部内的关系网络，其中包含 34 个节点（成员）和 156 条边（关系），每个节点有一个 34 维的特征向量和一个类标签。

edge_index

• edge_index：表示图的连接关系（start,end两个序列）
• node features：每个点的特征
• node labels：每个点的标签
• train_mask：有的节点木有标签（用来表示哪些节点要计算损失）

edge_index = data.edge_index
print(edge_index.t())

解析上面代码:

这两行代码主要关注图中的边信息，特别是 edge_index 属性。在 PyTorch Geometric（一个流行的图神经网络库）中，边的信息通常以 edge_index 的形式存储。

1. edge_index = data.edge_index:
   这行代码从 data 对象中取出 edge_index 属性并将其赋值给一个新的变量 edge_index。在 PyTorch Geometric 中，edge_index 是一个表示图中所有边的张量。

   edge_index 的维度为 [2, E]，其中 E 是图中边的数量。每一列代表一条边，其中第一行的值是边的起始节点，第二行的值是边的终止节点。

   例如，考虑以下 edge_index:

   tensor([[0, 2, 2],
           [1, 0, 3]])
   

   这表示图中有三条边：从节点0到节点1、从节点2到节点0、从节点2到节点3。

2. print(edge_index.t()):
   这行代码首先使用 .t() 方法转置 edge_index 张量，然后打印它。转置操作会将 [2, E] 维度的张量变成 [E, 2] 维度。

   继续上面的例子，转置后的张量为:

   tensor([[0, 1],
           [2, 0],
           [2, 3]])
   

   这使得每一行代表一条边，其中第一个值是边的起始节点，第二个值是边的终止节点。这种表示方式更直观，也更容易阅读，尤其是当边的数量非常多时。

总之，这两行代码从图数据对象中提取边的信息并以更易读的格式打印出来。

使用networkx可视化展示

from torch_geometric.utils import to_networkx

G = to_networkx(data, to_undirected=True)
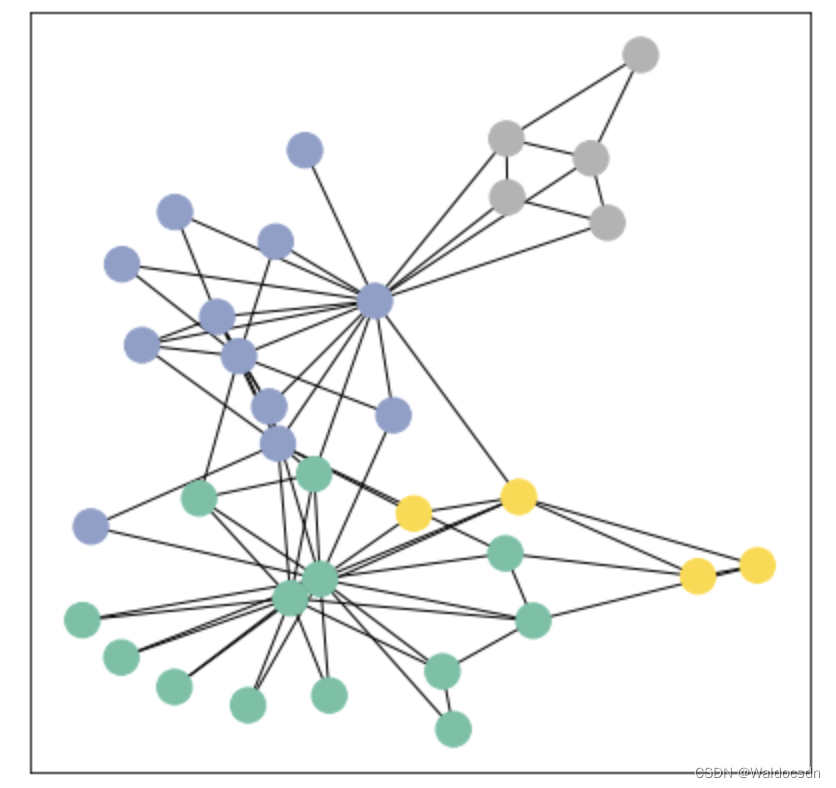
visualize_graph(G, color=data.y)

输出如下:

解析上面代码:
这段代码的目的是将 PyTorch Geometric 的图数据转换为 NetworkX 的图格式，并使用前面定义的 visualize_graph 函数将其可视化。以下是对代码的详细解析：

1. 导入所需工具:

   from torch_geometric.utils import to_networkx
   

   这行代码从 torch_geometric.utils 中导入了 to_networkx 函数，这个函数能够将 PyTorch Geometric 的图数据转换为 NetworkX 的图格式。

2. 将图数据转换为 NetworkX 格式:

   G = to_networkx(data, to_undirected=True)
   

   • 这里，to_networkx(data, to_undirected=True) 将 PyTorch Geometric 的图数据 data 转换为 NetworkX 的图 G。参数 to_undirected=True 表示即使原始图数据可能是有向的，我们也希望得到一个无向图。

3. 可视化转换后的图:

   visualize_graph(G, color=data.y)
   

   • 调用前面定义的 visualize_graph 函数来可视化 NetworkX 图 G。
   • 参数 color=data.y 意味着节点的颜色是基于 data.y 中的标签数据的。这样，不同的节点标签会被赋予不同的颜色，从而在可视化中可以轻松地区分它们。

综上所述，这段代码首先将 PyTorch Geometric 格式的图数据转换为 NetworkX 格式的图，然后使用给定的节点标签为该图上色并进行可视化。这种可视化通常很有助于理解图的结构和节点间的关系，尤其是当节点标签有意义时（例如，表示不同的社区或类别）。

Graph Neural Networks 网络定义：

• GCN layer (Kipf et al. (2017)) 定义如下：

x v ( ℓ + 1 ) = W ( ℓ + 1 ) ∑ w ∈ N ( v )   ∪   { v } 1 c w , v ⋅ x w ( ℓ ) \mathbf{x}_v^{(\ell + 1)} = \mathbf{W}^{(\ell + 1)} \sum_{w \in \mathcal{N}(v) \, \cup \, \{ v \}} \frac{1}{c_{w,v}} \cdot \mathbf{x}_w^{(\ell)} xv(ℓ+1)​=W(ℓ+1)w∈N(v)∪{v}∑​cw,v​1​⋅xw(ℓ)​

• PyG 文档 GCNConv

import torch
from torch.nn import Linear
from torch_geometric.nn import GCNConv


class GCN(torch.nn.Module):
    def __init__(self):
        super().__init__()
        torch.manual_seed(1234)
        self.conv1 = GCNConv(dataset.num_features, 4) # 只需定义好输入特征和输出特征即可
        self.conv2 = GCNConv(4, 4)
        self.conv3 = GCNConv(4, 2)
        self.classifier = Linear(2, dataset.num_classes)

    def forward(self, x, edge_index):
        h = self.conv1(x, edge_index) # 输入特征与邻接矩阵（注意格式，上面那种）
        h = h.tanh()
        h = self.conv2(h, edge_index)
        h = h.tanh()
        h = self.conv3(h, edge_index)
        h = h.tanh()  
        
        # 分类层
        out = self.classifier(h)

        return out, h

model = GCN()
print(model)

输出如下:

GCN(
  (conv1): GCNConv(34, 4)
  (conv2): GCNConv(4, 4)
  (conv3): GCNConv(4, 2)
  (classifier): Linear(in_features=2, out_features=4, bias=True)
)

解析上面的代码:

代码定义了一个简单的图卷积网络（GCN）模型。详细分析这段代码:

1. 导入必要的库和模块:

   import torch
   from torch.nn import Linear
   from torch_geometric.nn import GCNConv
   

   这些库和模块是构建模型所必需的。

2. 定义 GCN 类:

   class GCN(torch.nn.Module):
   

   通过继承 torch.nn.Module，我们定义了一个新的神经网络模型类 GCN。

3. 初始化方法:

   def __init__(self):
       super().__init__()
       torch.manual_seed(1234)
       ...
   

   • 使用 super().__init__() 调用父类的初始化方法。
   • torch.manual_seed(1234) 设置随机种子，以确保模型的权重初始化是确定的。

4. 定义图卷积层和分类器:

   • self.conv1 = GCNConv(dataset.num_features, 4): 定义第一个图卷积层，它将输入特征（即图中节点的特征数，这里为34）映射到4个特征。
   • 接下来的两个图卷积层 self.conv2 和 self.conv3 进一步对特征进行转换。
   • self.classifier = Linear(2, dataset.num_classes): 这是一个线性分类层，用于将最后一个图卷积层的输出（2个特征）映射到目标类别的数量（这里是4）。

5. 定义前向传播方法:

   def forward(self, x, edge_index):
       ...
       return out, h
   

   • 这定义了如何对输入数据进行操作以获得模型的输出。
   • 数据通过三个图卷积层，并在每层后应用双曲正切激活函数 tanh。
   • 输出经过分类器并返回。

6. 实例化模型并打印:

   model = GCN()
   print(model)
   

   这些行实例化上面定义的 GCN 类并打印模型的结构。输出显示了模型包含的各个层及其配置。

输出的解析：

GCN(
  (conv1): GCNConv(34, 4)
  (conv2): GCNConv(4, 4)
  (conv3): GCNConv(4, 2)
  (classifier): Linear(in_features=2, out_features=4, bias=True)
)

这个输出描述了 GCN 模型的结构。它有三个图卷积层和一个线性分类器。例如，(conv1): GCNConv(34, 4) 表示第一个图卷积层接受34个特征作为输入并输出4个特征。最后，线性分类器将2个特征映射到4个输出类别。

总体而言，这段代码定义了一个三层的图卷积网络，并为每个节点生成分类分数。

输出特征展示

• 最后不是输出了两维特征嘛，画出来看看长啥样
• 但是，但是，现在咱们的模型还木有开始训练。。。

model = GCN()

_, h = model(data.x, data.edge_index)
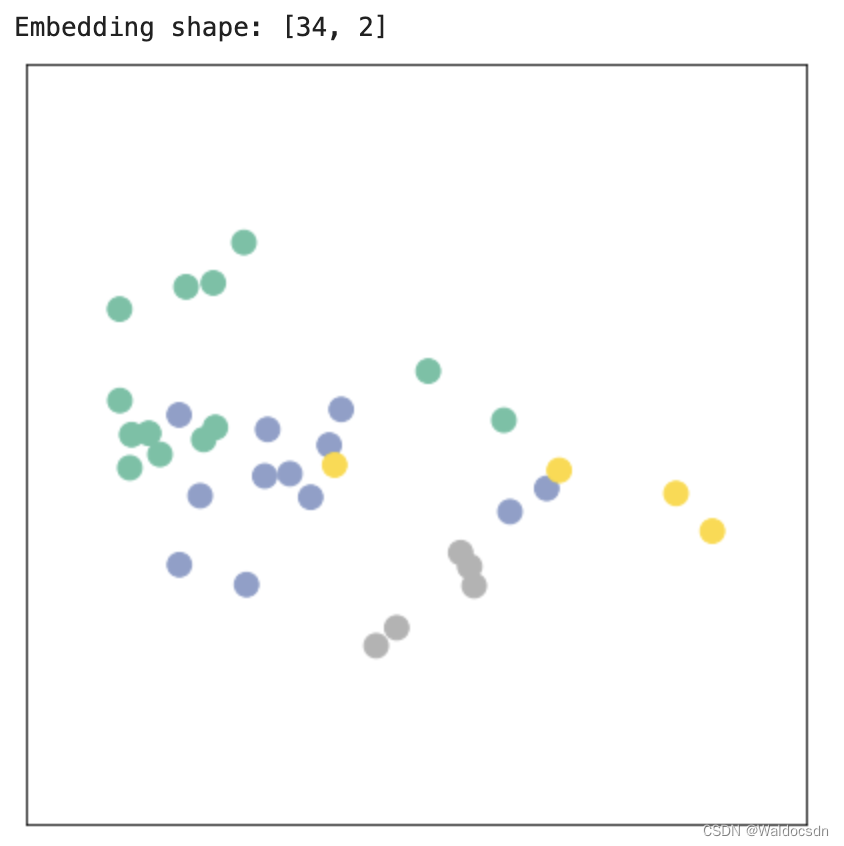
print(f'Embedding shape: {list(h.shape)}')

visualize_embedding(h, color=data.y)

输出如下：

解析上面的代码:

这段代码主要关注了两件事：首先，它在一个图上运行定义的 GCN 模型来获取节点嵌入；然后，它使用一个可视化函数来显示这些嵌入。以下是对代码的详细解析：

1. 模型实例化:

   model = GCN()
   

   这行代码创建了 GCN 类的一个新实例。该模型已经在前面的代码中被定义，并且它包含了三个图卷积层和一个线性分类器。

2. 模型前向传播:

   _, h = model(data.x, data.edge_index)
   

   这行代码调用了 GCN 模型的前向传播方法，传入节点特征 data.x 和边索引 data.edge_index 作为参数。这两个参数来源于 data，这是一个 PyTorch Geometric 图数据对象。

   输出是一个元组，其中第一个元素 _ 是模型的主要输出（分类得分），而第二个元素 h 是模型的最后一个图卷积层的输出，代表节点的嵌入。

3. 打印嵌入的形状:

   print(f'Embedding shape: {list(h.shape)}')
   

   这行代码将嵌入张量 h 的形状打印出来。这有助于我们了解嵌入的维度，通常这是 [节点数, 嵌入维度]。

4. 可视化嵌入:

   visualize_embedding(h, color=data.y)
   

   使用之前定义的 visualize_embedding 函数，这行代码将嵌入 h 可视化为一个散点图。这个散点图中的每个点都代表一个节点，位置由其嵌入决定。点的颜色基于 data.y，这通常代表节点的标签或类别。

总结：这段代码运行了一个图卷积网络模型，取得了节点的嵌入，并将这些嵌入可视化。这种可视化有助于我们理解模型如何将节点分布在嵌入空间中，以及节点间的相似性和差异性。

训练模型(semi-supervised)

import time

model = GCN()
criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.

def train(data):
    optimizer.zero_grad()  
    out, h = model(data.x, data.edge_index) #h是两维向量，主要是为了咱们画个图 
    loss = criterion(out[data.train_mask], data.y[data.train_mask])  # semi-supervised
    loss.backward()  
    optimizer.step()  
    return loss, h

for epoch in range(401):
    loss, h = train(data)
    if epoch % 10 == 0:
        visualize_embedding(h, color=data.y, epoch=epoch, loss=loss)
        time.sleep(0.3)

解析上面的代码:

这段代码定义了训练流程并执行了400个训练周期。接下来，我们将逐步解析代码的每一部分。

1. 初始化模型和工具:

   model = GCN()
   criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
   optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.
   

   • model = GCN(): 创建 GCN 类的一个新实例，之前已经定义。
   • criterion: 定义了损失函数，这里使用的是交叉熵损失，适用于分类问题。
   • optimizer: 定义了优化器，用于更新模型的权重。这里使用的是Adam优化器，学习率设为0.01。

2. 定义训练函数:

   def train(data):
       ...
       return loss, h
   

   这个函数定义了模型的一次训练步骤，并返回损失和节点嵌入。具体步骤如下：

   • optimizer.zero_grad(): 清除之前梯度的残留。
   • out, h = model(data.x, data.edge_index): 对模型进行前向传播。
   • loss = criterion(out[data.train_mask], data.y[data.train_mask]): 计算损失。由于这是一个半监督学习任务，我们只在具有标签的节点上计算损失，这些节点由train_mask指示。
   • loss.backward(): 基于计算的损失进行反向传播，计算梯度。
   • optimizer.step(): 使用优化器更新模型的权重。

3. 训练循环:

   for epoch in range(401):
       loss, h = train(data)
       ...
   

   这个循环执行了401个训练周期。在每个周期，它都会调用上面定义的train函数，获取损失和嵌入。

4. 可视化:

   if epoch % 10 == 0:
       visualize_embedding(h, color=data.y, epoch=epoch, loss=loss)
       time.sleep(0.3)
   

   每10个周期，代码会调用之前定义的visualize_embedding函数，显示节点的嵌入。time.sleep(0.3)意味着每次可视化之间会有0.3秒的暂停，使得可视化的变化不会过于迅速，这样我们可以更容易地观察节点嵌入的变化情况。

总的来说，这段代码定义了图卷积网络模型的训练过程，并在每10个训练周期后进行嵌入可视化，这样我们可以看到模型是如何逐渐学习将相似的节点放在嵌入空间的相近位置的。

回顾

综述

在训练开始时，嵌入（由h表示）可能是随机的或是在嵌入空间中均匀分布的。这意味着，在散点图中，具有不同标签的节点可能会混在一起，没有明显的聚类。

随着训练的进行，模型会尝试将相似的节点（基于它们的特征和它们在图中的位置）放在嵌入空间中的相近位置，并将不相似的节点分开。这在可视化中表现为：

1. 具有相同标签的节点开始聚集在一起。
2. 不同的聚类或类别之间形成了明确的边界。

在多次迭代之后，如果模型被成功地训练，我们应该能看到几个清晰的聚类，其中每个聚类代表一种类别的节点。在KarateClub数据集中，由于有4个类，我们期望看到4个聚类。

---

回顾和总结上面的代码和实践。

1. 目标:

在KarateClub数据集上使用图卷积网络 (GCN) 进行节点分类。

2. 数据加载:

首先加载了KarateClub数据集，这是一个经典的小型图数据集。它描述了一个空手道俱乐部中34个成员之间的关系，目标是根据其社交网络关系预测每个成员的团体归属。

3. 数据可视化:

利用networkx库和提供的工具函数，将图数据可视化为网络结构图。

4. 模型定义:

定义了一个简单的GCN模型，它包括三个GCNConv层，用于学习图中节点的嵌入表示，以及一个线性分类器，用于将这些嵌入映射到预测的类别。

5. 嵌入可视化:

在模型定义后，立即进行了一次前向传播，并使用提供的工具函数可视化了初始的节点嵌入。这提供了一个参考点，了解模型训练前节点嵌入的初始状态。

6. 模型训练:

• 设定了交叉熵损失和Adam优化器。
• 定义了一个train函数来描述单次训练迭代的流程。
• 在400个周期中进行了模型的训练，并每10个周期可视化节点嵌入，以观察模型是如何逐步更新和优化嵌入的。

总结:

我们成功地将图神经网络应用于KarateClub数据集的节点分类任务。首先加载和可视化数据，然后定义了一个GCN模型，之后可视化了初始的节点嵌入。在接下来的训练过程中，观察了随着训练的进行，嵌入如何逐渐形成聚类，以便使具有相同标签的节点更接近。这个实践展示了图神经网络在节点分类任务上的工作方式和其效果。

补充

关于嵌入（由h表示）:

嵌入（Embedding）在深度学习和自然语言处理中是一个非常常见的概念。嵌入是将某种类型的数据（如单词、节点、用户或其他实体）转换为固定大小的向量，这样机器学习模型可以更容易地处理它。

代码中，嵌入（由h表示）特指图的节点嵌入。这意味着每个图中的节点都被转换为一个向量。这些向量捕捉了节点的特征和其在图中的结构位置。

以下是关于嵌入的一些详细点：

1. 捕捉信息：嵌入向量通常被设计为捕捉关于原始数据的有意义的信息。例如，在词嵌入中，相似的单词会有相似的嵌入。

2. 固定大小：不论原始数据的大小或形式如何，嵌入向量都有固定的长度。这对于机器学习模型非常有用，因为它们需要固定大小的输入。

3. 图节点嵌入：在图神经网络（如GCN）中，节点嵌入捕捉了节点的特征信息以及其在图中的邻接关系。相邻或相似的节点可能会有相似的嵌入。

4. 可视化：由于嵌入是高维数据的向量表示，它们可以用于可视化。在代码中，h的每个节点嵌入是一个二维向量，这使得它们可以直接在平面上绘制。这种可视化有助于我们理解模型是如何在嵌入空间中组织节点的。

在上下文中，h是图卷积网络（GCN）的输出，它为图中的每个节点提供一个二维嵌入。这些嵌入向量随着模型的训练而更新，以更好地反映节点的特征和其在图中的位置。