文章目录
- 前言
- 1. 二叉树里面的双指针
- 1.1 判断两棵树是否相同
- 1.2 对称二叉树
- 1.3 合并二叉树
- 2. 路径专题
- 2.1 二叉树的所有路径
- 2.2 路径总和
- 3. 翻转的妙用
- 总结
前言
提示:人类的底里是悲伤,我们都在用厚重的颜料,覆盖那些粗糙的线稿。--张皓宸《抬头看二十九次月亮》
前面的练习才是开始,这理才是真正的进入算法的门槛,来迎接下一波挑战吧。
1. 二叉树里面的双指针
所谓的双指针就是定义了两个变量,在二叉树中有时候也需要至少定义两个变量才能解决问题,这两个指针可能针对一颗树,也可能针对两棵树,我们这里就称他为”双指针“吧。这些问题一般是关于对称、翻转、合并等类型相关,我们接下来就看一些高频出现的问题吧。
1.1 判断两棵树是否相同
参考题目介绍:100. 相同的树 - 力扣(LeetCode)
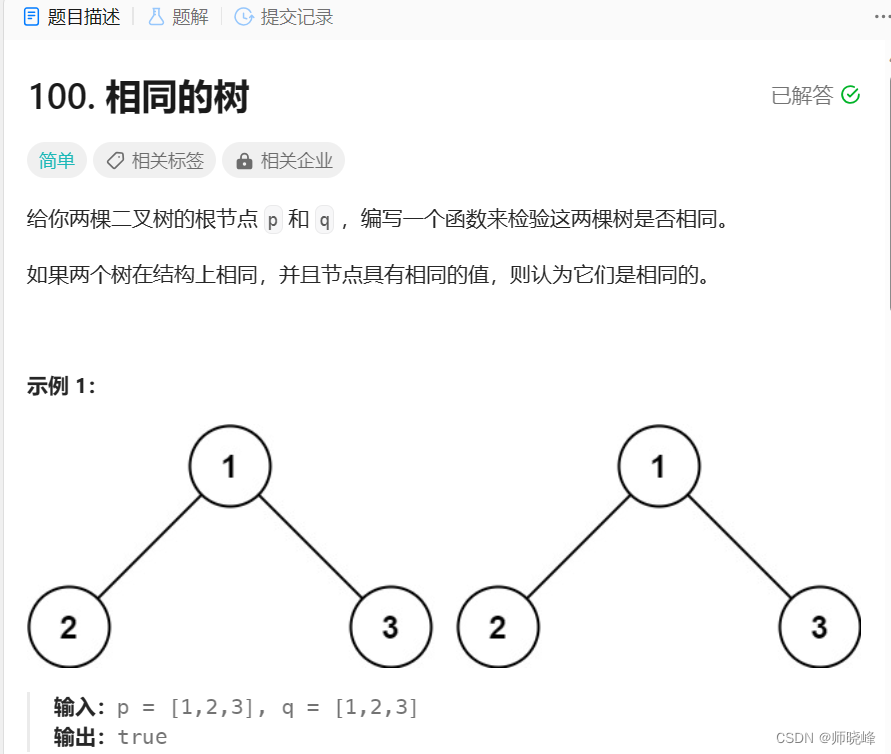
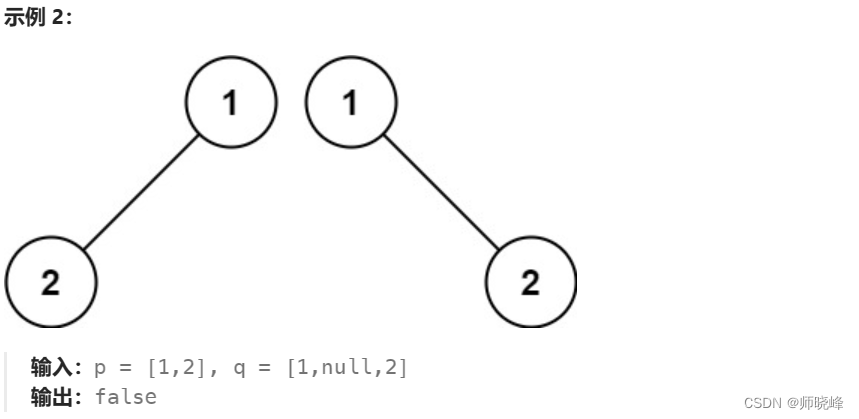
这个貌似很好就容易实现了,两个二叉树同时进行前序遍历,先判断根节点是否相同,如果相同再分别判断左右子节点是否相同,判断的过程中只要存在一个不相同的就返回false,如果全部相同就返回true。其实也就是这样的。
/**
* 判断两个二叉树是否相同
* @param p
* @param q
* @return
*/
public static boolean isSameTree(TreeNode p, TreeNode q) {
// 校验参数
// 如果两个节点为空 肯定相同
if (p == null && q == null) {
return true;
}
// 如果两个中有一个不为空 一定不相同
if (p == null || q == null) {
return false;
}
// 当然如果 数据不同 一定不相同
if(p.val != q.val){
return false;
}
// 走到这一步 说明p和q的节点是完全相同的,然后接着遍历
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
这里你也可以试一试广度优先,这样写会怎么样,感兴趣可以试试。
1.2 对称二叉树
参考题目介绍:101. 对称二叉树 - 力扣(LeetCode)
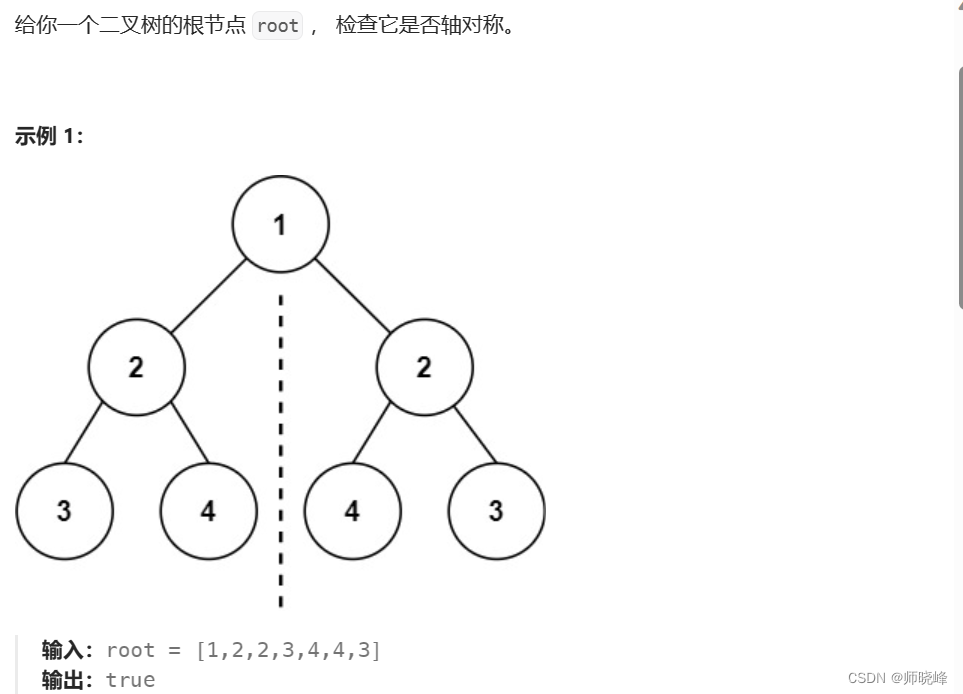

如果树是镜像的,看看这个图,更加清晰:
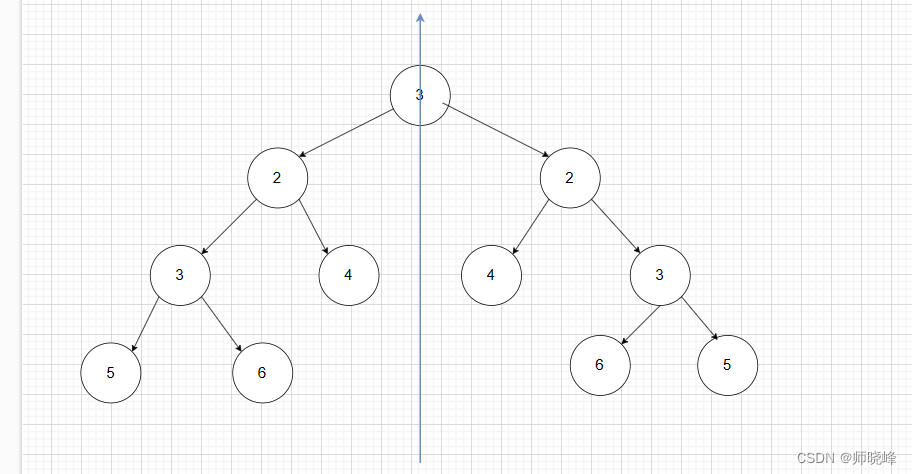
因为我们要通过递归函数的返回值来判断这两个子树内测节点是否相同,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。这里的关键还是比较和如何处理结束的条件。单层递归的逻辑就是处理左右节点不为空且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子
- 比较二叉树内侧是否对称:传入左节点的右孩子,右节点的左孩子
- 如果左右都对称就返回true,有一侧不对称就返回false。
接下来就是合并和简化代码的过程了:
/**
* 判断是否是一颗对称的二叉树
* @param root
* @return
*/
public static boolean isSymmetric(TreeNode root) {
// 校验参数
if (root == null){
return true;
}
return check(root.left,root.right);
}
private static boolean check(TreeNode p, TreeNode q) {
if (p == null && q == null){
return true;
}
if (p == null || q == null){
return false;
}
if (p.val != q.val){
return false;
}
return check(p.left, q.right) && check(p.right, q.left);
}
1.3 合并二叉树
参考题目介绍:617. 合并二叉树 - 力扣(LeetCode)

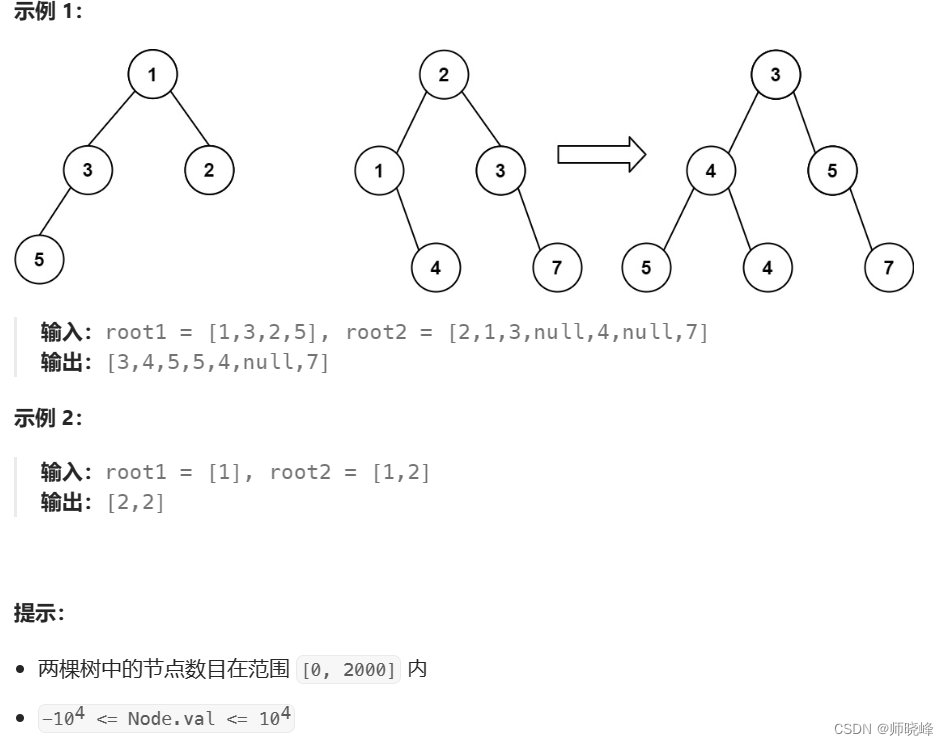
两个二叉树的对应节点可能存在一下三种情况,对于每种情况的使用不同的合并方式。
- 如果两个二叉树的对应节点都为空,则合并的二叉树的对应节点也为空;
- 如果两个二叉树的对应节点只有一个为空空,则合并后的二叉树的对应节点为其中的非空节点;
- 如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应值之和,此时需要显性合并两个节点。
对一个节点进行合并之后,还要对该节点的左右子树分别进行合并;
代码如下:
/**
* 合并两个二叉树
*
* @param t1
* @param t2
* @return
*/
public static TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
// 校验参数
if (t1 == null){
return t2;
}
if (t2 == null){
return t1;
}
// 建立一个新的树root
TreeNode merged = new TreeNode(t1.val + t2.val);
merged.left = mergeTrees(t1.left,t2.left);
merged.right = mergeTrees(t1.right,t2.right);
return merged;
}
如果这到题目没有想明白的话,就带入例子看看验证一下。
看了这么多,我们是不是也可以造一个提来看看:前面我们研究了两颗树相等和一棵树对称的情况,我们这里可以造一个判断题,怎么证明两棵树是否对称。想一下这个要怎么写💡
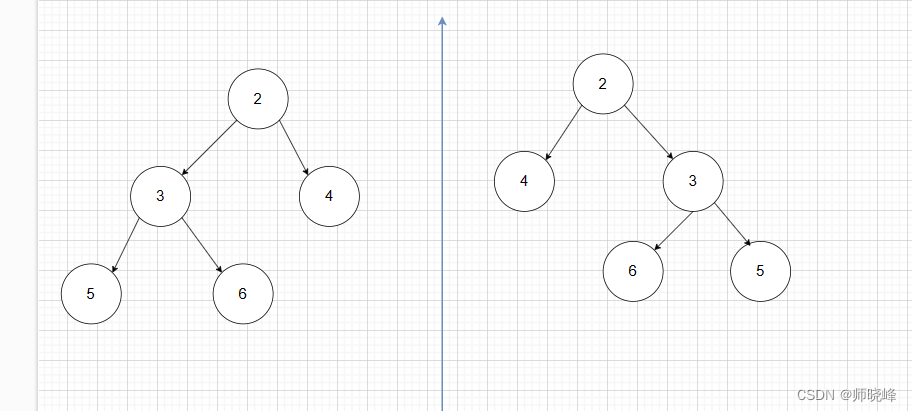
2. 路径专题
关于二叉树有些题目与路径有关,我们这里好好看下。回溯这个看起来头疼的问题,我们先放在后面,看看这个路径专题哈哈🥰
2.1 二叉树的所有路径
参考题目介绍:257. 二叉树的所有路径 - 力扣(LeetCode)

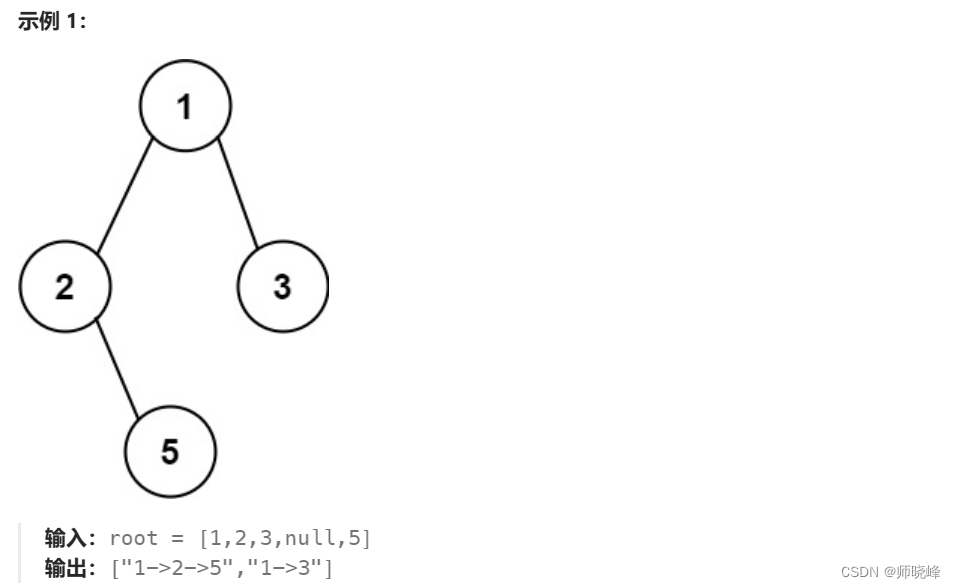
我们可以注意有几个叶子节点,有几个就说明有几条路径,这么问题就转换成了怎么找叶子节点了。我们知道深度优先搜索就是从根节点出发一直寻到叶子节点,这里我们可以先判断当前节点是不是叶子节点,再决定是不是向下走,如果是叶子节点,我们就增加一条路径,就像下图一样。
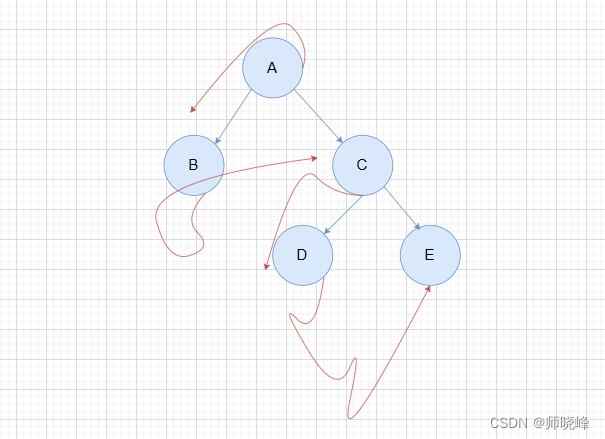
这里还有个问题,当得到一个叶子节点容易,这时候怎么知道它所在的完整路径是什么呢?例如上图中的D之后,怎么知道前面还有A和C呢?这里简单,我们增加一个String类型的变量,访问每个节点的时候先将他存入String中,到叶子节点的时候再添加到集合中:
具体代码如下:
/**
* 二叉树的所有路径
* @param root
* @return
*/
public static List<String> binaryTreePaths(TreeNode root) {
// 创建空间
List<String> res = new ArrayList<String>();
// 广度优先搜索
dfs(root, "", res);
return res;
}
private static void dfs(TreeNode root, String path, List<String> res) {
// 终止条件
if (root == null) {
return;
}
// 到达叶子节点
if (root.left == null && root.right == null) {
res.add(path + root.val);
return;
}
// 分别遍历左右子树
dfs(root.left, path + root.val + "->", res);
dfs(root.right, path + root.val + "->", res);
}
这个题目是回溯的基础入门问题,我们后面再讲,感兴趣的同学可以带入例子看看。
2.2 路径总和
参考题目介绍:112. 路径总和 - 力扣(LeetCode)

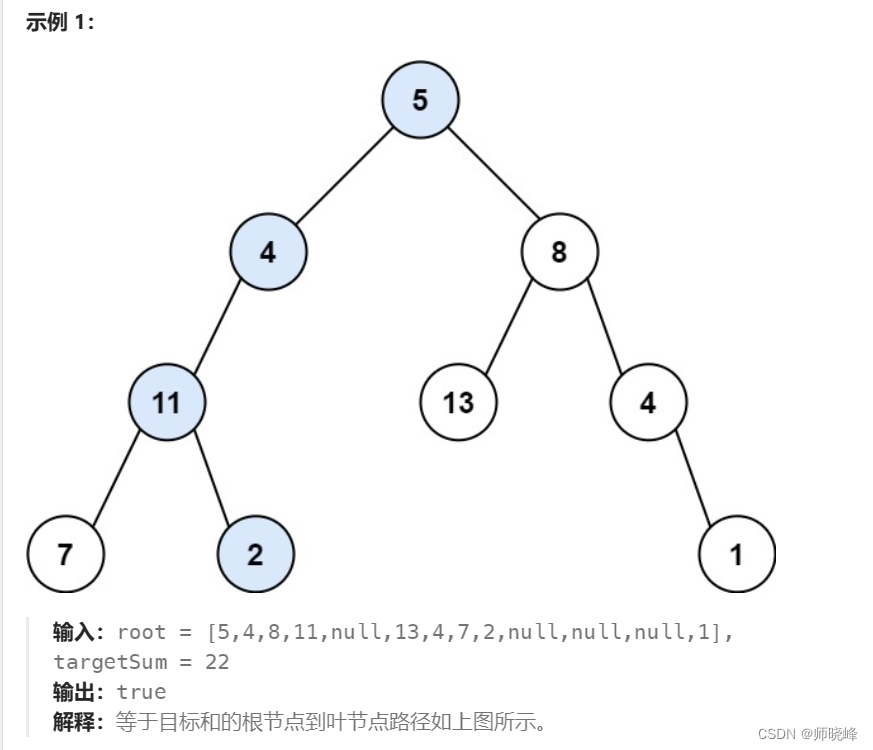
本题目询问是否存在从当前节点root到叶子节点的路径,满足其路径和为sun,假定从根节点到当前节点的值之和为val,我们可以将这个大问题转换成为一个小问题:是否存在从当前节点的子节点到叶子的路径,其满足路径和为sum - val。
不难看出这个问题满足递归的性质,若当前节点就是叶子节点,那么我们直接判断sum是否等于val即可(因为路径和已经确定,就是当前节点的值,我们只要判断该路径和是否满足条件)。若当前节点不是叶子节点,需要继续递归询问它的子节点是否满足条件。
代码就好写多了😎:
/**
* 路径总和
*
* @param root
* @param sum
* @return
*/
public static boolean hasPathSum(TreeNode root, int sum) {
// 终止条件
if(root == null){
return false;
}
if (root.left == null && root.right == null){
return sum == root.val;
}
// 接着遍历左右子树
boolean left = hasPathSum(root.left,sum - root.val);
boolean right = hasPathSum(root.right,sum - root.val);
return left || right;
}
学了这道题,感性取的话可以挑战一下路径总和II。这里必考虑回溯问题
推荐题目⭐⭐⭐⭐
113. 路径总和 II - 力扣(LeetCode)
3. 翻转的妙用
参考题目介绍:226. 翻转二叉树 - 力扣(LeetCode)
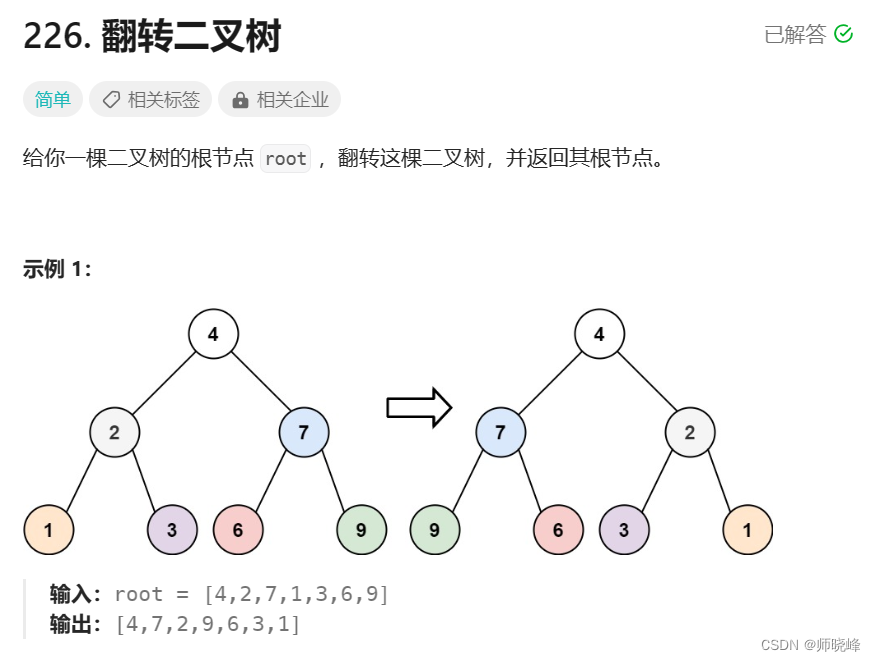
这个题目同类型题:剑指 Offer 27. 二叉树的镜像 - 力扣(LeetCode)简直是一摸一样。当然了,根据上图,我们可以发现想要翻转树,就是把每个节点的左右孩子交换一下。关键在于遍历顺序,前中后你觉的那个更适合呢?遍历的过程中取翻转每一个节点的左右孩子就可以达到整体翻转的效果。注意只要把每一个节点的左右孩子翻转一下就可以达到整体翻转的效果。
这是一道很经典的二叉树问题。显然,我们从根节点开始,递归对树进行遍历,并从叶子节点先开始翻转。如果当前遍历到的节点root的左右两颗子树都已经翻转过,那么我们只需要交换两个子树的位置,就可以完成以root为根节点的整棵树的翻转。
话不多说先看看前序交换怎么实现的,代码如下:
/**
* 前序遍历的二叉树翻转
* @param root
* @return
*/
public TreeNode invertTree(TreeNode root) {
// 终止条件
if (root == null){
return null;
}
// 先处理根节点
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 然后左右子树
invertTree(root.left);
invertTree(root.right);
return root;
}
那么后序遍历呢?
/**
* 后序遍历的二叉树翻转
* @param root
* @return
*/
public TreeNode invertTree(TreeNode root) {
// 终止条件
if (root == null) {
return null;
}
// 先左右
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right = left;
return root;
}
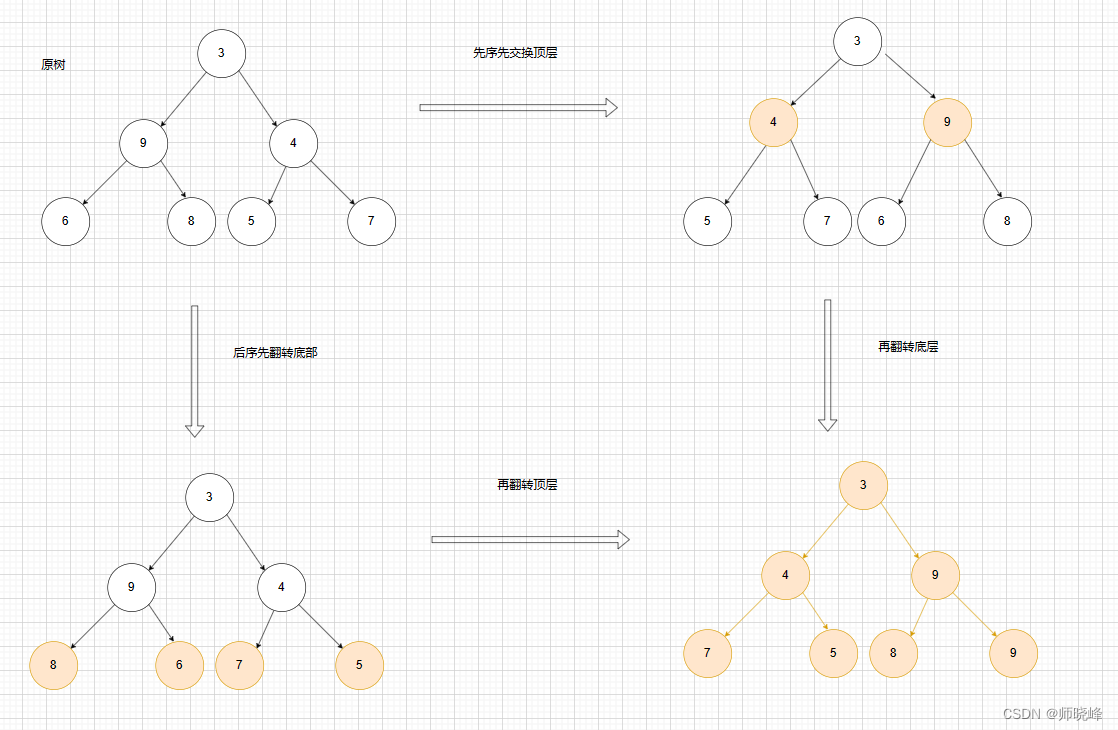
这道题目使用前序和后序遍历都可以,你猜对了吗?💕主要区别就是,前序是先处理子节点,属于自顶向下,后序是先处理叶子节点最后处理自己,属于自下而上的。我们来看这个图:
当然了,本题还可以使用层序遍历实现,核心思想就是元素出队时,先将其左右孩子不直接入队,而是反转后再放进去,顺便也看下代码吧:
/**
* 层序遍历的二叉树翻转
*
* @param root
* @return
*/
public TreeNode invertTree(TreeNode root) {
// 参数校验
if (root == null) {
return null;
}
// 创建空间
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 根节点入队列
queue.offer(root);
// 只要队列不为空 就一直遍历
while(!queue.isEmpty()){
// 每次从队列中拿到一个节点,并交换这个节点的左右子树
TreeNode temp = queue.poll();
TreeNode left = temp.left;
temp.left = temp.right;
temp.right = left;
// 如果当前节点的左子树不空 放入队列等待处理
if (temp.left != null){
queue.offer(temp.left);
}
// 如果当前节点的右子树不空 放入队列等待处理
if (temp.right != null){
queue.offer(temp.right);
}
}
return root;
}
总结
提示:二叉树的双指针问题;路径问题;翻转问题;回溯初始