文章目录

1. 基础概念
- 🍑 内部排序和外部排序
2. 直接插入排序
3. 动图演示
4. 代码实现
5. 性能分析

无论是日常生活还是很多科学领域当中，排序都是会经常面对的问题，比如按成绩对学校的学生排序，按薪水多少对公司员工排序等。

根据在排序过程中待排序的数据是否全部被载入到内存中，排序分为内部排序和外部排序。下面各种排序算法涉及的主要是内部排序，包含各种经典的内部排序算法。

将按照对 数据操作方式 的不同来分类讲解。

在这里插入图片描述

1. 基础概念

所谓排序（Sort），就是将一组数据（也称元素），按照一定的规则调换位置，使这组数据按照递增或递减的顺序重新排列。例如数据库中有一个 “学生表”，可以针对该表中的 “年龄” 字段进行排序，那么这个待排序的字段就称为键（key）或者关键字。排序一般是为了让查找数据的效率变得更高。

这里涉及一个排序算法的稳定性问题。依旧以 “学生表” 为例，假如表中数据如下：

在这里插入图片描述

在上图所示的学生表中，需要针对表中的 “年龄” 字段（键）按照某种排序算法进行递减或者递增排序。此时（排序前）张三和赵六的年龄都是 27 岁且张三这条记录位于赵六之前，而在排序后，如果张三这条记录依旧位于赵六之前，那我们就说这种排序算法是稳定的，如下图所示：

在这里插入图片描述

反之，如果排序后赵六这条记录位于张三之前，那我们就说这种排序算法是不稳定的，如下图所示：

在这里插入图片描述

所以，所谓 稳定的排序算法，指的就是关键字相同的元素在排序后相对位置不变。针对排序算法的稳定性有两点说明：

有些排序算法，基于其实现的原理，确实是无法做到稳定，这种算法当然称为不稳定。
有些排序算法，是可以做到稳定的。但是，如果稍微调整一下它的实现代码，让它变得不稳定也是很容易的。
当无法判断一个算法是否稳定时，可以书写测试代码来进行稳定性测试。

🍑 内部排序和外部排序

在排序算法实现时，虽然很多时候都是用整数进行举例，但在真正的项目中，往往要排序的并不是单纯的数字，而是一组对象，按照对象的某个关键字来排序，所以排序的稳定性也是一个必须要考虑的问题。

想象一下，两个用户在某个电子商城中购买了相同的商品，他们的下单时间一个在前一个在后，如果按照订单中商品价格排序，那么这两张订单因为购买的是相同的商品，价格相同，所以排序后应该会相邻，但因为采用稳定的排序算法，所以排序后这两个订单依旧会按照原来下单的时间顺序排列。

根据在排序过程中待排序的数据是否全部被载入到内存中，排序分为 内部排序（内排序） 和 外部排序（外排序）。

内部排序 是指：在整个排序过程中，待排序的所有数据（记录）都被载入到内存中。

外部排序 是指：在整个排序过程中，因为排序的数据太多（比如大数据）而不能同时载入到内存中，导致整个的排序过程需要在内存和外存（比如磁盘）之间进行多次数据交换。因为磁盘和内存的读写速度相比往往要慢上数十甚至数百倍，所以外部排序往往需要尽量减少磁盘的读写次数。

这些经典的内部排序算法有好多种，每种排序算法都有相应的优缺点，适合在不同的情况下使用。而这些算法的分类方式也有很多种，比如按照数据操作方式来划分，按照时间复杂度来划分等。

大部分经典排序算法都仅适用于顺序存储的线性表，而不太适用于链式存储的线性表。对于大多数排序算法在排序过程中有两种基本操作：

比较两个关键字的大小
将记录从一个位置移动到另外一个位置

一般来说，比较两个关键字大小是必须的，但将记录从一个位置移动到另外一个位置也许可以通过一些变通的方式来实现，从而提高排序算法的执行效率。而效率对于排序算法当然是最重要的。

2. 直接插入排序

所谓 插入类 排序，就是向有序序列（已经排好序的序列）中依据关键字的比较结果寻找合适的位置，插入新的记录，构成新的有序序列，直至所有记录插入完毕。

插入类排序可以细分为很多种，每种之间的差别主要体现在插入位置的查找以及插入新数据导致原有数据的移动方面。我们先来看第一种。

直接插入排序： 每次将一个记录按其关键字的大小插入到已经排好序的序列中，直至全部记录插入完毕。这种排序方式将待排数据依次和数组中已经排好序的记录进行比较并确定自己的位置。

假设现在有 10 个元素的整型数组：int arr[] = {16, 1, 45, 23, 99, 2, 18, 67, 42, 10}，现在，我们希望对这个数组中的元素进行从小到大排序。

根据直接插入排序算法的思想，我们首先认为数组中的第 1 个元素（16）包含在已经排好序的序列中。然后从数组中的第 2 个元素开始，依次针对数组中的元素寻找合适的位置插入到已经排好序的序列中就行了。

所以，就会有下面的操作步骤：

先看 1，1 比 16 小，所以 1 插入到 16 之前，16 后移。这是因为已经排好序的序列中目前只有 16，所以只需要将 16 后移，数组 arr 目前的情形是：{1, 16, 45, 23, 99, 2, 18, 67, 42, 10}。
接着看 45，45 比 1 和 16 都大所以 45 位置不动，数组 arr 目前的情形是：{1, 16, 45, 23, 99, 2, 18, 67, 42, 10}。
接着看 23，23 比 16 大但比 45 小，所以 23 插入到 45 之前，45 后移，数组 arr 目前的情形是：{1, 16, 23, 45, 99, 2, 18, 67, 42, 10}。
接着看 99，99 目前最大，所以位置不动，数组 arr 目前的情形是：{1, 16, 23, 45, 99, 2, 18, 67, 42, 10}。
接着看 2，2 比 1 大但比 16 小，所以 2 插入到 16 之前，16、23、45、99 依次后移，数组 arr 目前的情形是：{1, 2, 16, 23, 45, 99, 18, 67, 42, 10}。
接着看 18，18 比 16 大但比 23 小，所以 18 插入到 23 之前，23、45、99 依次后移，数组 arr 目前的情形是：{1, 2, 16, 18, 23, 45, 99, 67, 42, 10}。
接着看 67，67 比 45 大但比 99 小，所以 67 插入到 99 之前，99 后移，数组 arr 目前的情形是：{1, 2, 16, 18, 23, 45, 67, 99, 42, 10}。
接着看 42，42 比 23 大但比 45 小，所以 42 插入到 45 之前，45、67、99 依次后移，数组 arr 目前的情形是：{1, 2, 16, 18, 23, 42, 45, 67, 99, 10}。
接着看 10，10 比 2 大但比 16 小，所以 10 插入到 16 之前，16、18、23、42、45、67、99 依次后移，数组 arr 目前的情形是：{1, 2, 10, 16, 18, 23, 42, 45, 67, 99}。

以上就是直接插入排序算法的完整工作过程描述。

把一个无序数组 {16, 1, 45, 23, 99, 2, 18, 67, 42, 10} 最终变得有序 {1, 2, 10, 16, 18, 23, 42, 45, 67, 99}，只需要从前向后遍历数组中的每个元素，再为每个元素找到合适的位置就可以了。

3. 动图演示

这里我对 21, 3, 6, 17, 12, 1, 49, 10, 45, 43 这组数据进行直接插入排序，每趟的排序过程如下：

在这里插入图片描述

4. 代码实现

直接插入排序的实现代码有很多种，比如有的资料会采用哨兵位的方式来实现。所谓哨兵位，就是在数据结构中留出一个特殊位置，避免在算法实现过程中引入临时变量。下面采用的是非哨兵的实现方式。

代码实现

//直接插入排序（从小到大）
template<typename T>
void InsertSort(T arr[], int len) {
	if (len <= 1) //不超过1个元素的数组，没必要排序
		return;
	
	for (int i = 1; i < len; ++i) //从第2个元素（下标为1）开始比较
	{
		if (arr[i] < arr[i - 1])
		{
			T temp = arr[i]; //暂存arr[i]值，防止后续移动元素时值被覆盖   
			int j;
			for (j = i - 1; j >= 0 && arr[j] > temp; --j) //检查所有前面排好序的元素
			{
				arr[j + 1] = arr[j]; //所有大于temp的元素都向后移动
			}
			arr[j + 1] = temp; //复制数据到插入位置，注意j因为被减了1，这里加回来
		}
	}
	return;
}

在主函数中，加入测试代码

int main()
{
	int arr[] = {16, 1, 45, 23, 99, 2, 18, 67, 42, 10}; 
	int len = sizeof(arr) / sizeof(arr[0]); //数组中元素个数
	InsertSort(arr, len); //对数组元素进行直接插入排序
	
	//输出排好序的数组中元素内容
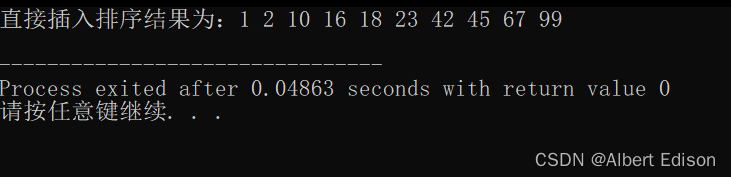
	cout << "直接插入排序结果为：";
	for (int i = 0; i < len; ++i) {
		cout << arr[i] << " ";
	}
	cout << endl;
	
	return 0;
}