LeetCode 1584. 连接所有点的最小费用【最小生成树】

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个 points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的曼哈顿距离：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

示例 1：

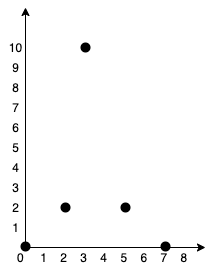
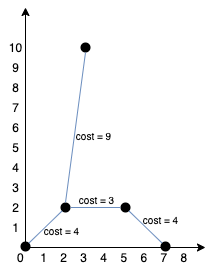
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：

输入：points = [[0,0]]
输出：0

提示：

1 <= points.length <= 1000
- -10^6 <= xi, yi <= 10^6
所有点 (x_i, y_i) 两两不同。

根据题意，我们得到了一张 $O (n)$ 个节点的完全图，任意两点之间的距离均为它们的曼哈顿距离。现在我们需要在这个图中取得一个子图，恰满足子图的任意两点之间有且仅有一条简单路径，且这个子图的所有边的总权值之和尽可能小。

能够满足任意两点之间有且仅有一条简单路径只有树，且这棵树包含 $O (n)$ 个节点。我们称这棵树为给定的图的生成树，其中总权值最小的生成树，我们称其为最小生成树。

解法 Kruskal算法

最小生成树有一个非常经典的解法： $\text{Kruskal}$ 。 $\text{Kruskal}$ 算法是一种常见并且好写的最小生成树算法，由 $\text{Kruskal}$ 发明。该算法的基本思想是从小到大加入边，是一个贪心算法。

其算法流程为：

将图 $G=\{V,E\}$ 中的所有边按照长度由小到大进行排序，等长的边可以按任意顺序。
初始化图 $G^{'}$ 为 $\{V, \varnothing \}$ ，从前向后扫描排序后的边，如果扫描到的边 $e$ 在 $G^{'}$ 中连接了两个相异的连通块,则将它插入 $G^{'}$ 中。
最后得到的图 $G^{'}$ 就是图 $G$ 的最小生成树。

在实际代码中，我们首先将这张完全图中的边全部提取到边集数组中（使用 struct 而非 vector<int> 存储每一条边，不然会超时，vector 的创建也需要一定时间），然后对所有边进行排序，从小到大进行枚举（当有了 $n - 1$ 条边后可提前退出对边集数组的扫描），每次贪心选边加入答案。使用并查集维护连通性，若当前边两端不连通即可选择这条边。

class Solution {
public:
    struct Edge {
        int i, j, w;
    };
    int minCostConnectPoints(vector<vector<int>>& points) {
       vector<Edge> edges;
       int n = points.size();
       for (int i = 0; i < n; ++i) {
           for (int j = 0; j < n; ++j) {
               int dx = abs(points[i][0] - points[j][0]);
               int dy = abs(points[i][1] - points[j][1]);
               edges.push_back({i, j, dx + dy});
           }
       }
       sort(edges.begin(), edges.end(), [&](const auto &a, const auto &b) {
           return a.w < b.w;
       });
        int total = 0;
        vector<int> fa(n, -1);
        function<int(int)> find = [&](int x) -> int { return fa[x] < 0 ? x : fa[x] = find(fa[x]); } ;
        auto merge = [&](int rx, int ry) {
            if (fa[rx] < fa[ry]) {
                fa[rx] += fa[ry];
                fa[ry] = rx;
            } else {
                fa[ry] += fa[rx];
                fa[rx] = ry;
            }
        };
        int num = 0;
        for (int i = 0; i < edges.size(); ++i) {
            int u = edges[i].i, v = edges[i].j;
            int ru = find(u), rv = find(v);
            if (ru != rv) {
                total += edges[i].w;
                merge(ru, rv);
                ++num; // 边数到达了n-1时可以提前退出
                if (num == n - 1) break;
            }
        }
        return total;
    }
};

复杂度分析：

时间复杂度： $O(n^2\log(n))$ ，其中 $O (n)$ 是节点数。一般 $\text{Kruskal}$ 是 $O(m\log m)$ 的算法，但本题中 $m=n^2$ ，因此总时间复杂度为 $O(n^2\log(n))$ 。
空间复杂度： $O(n^2)$ ，其中 $O (n)$ 是节点数。并查集使用 $O (n)$ 的空间，边集数组需要使用 $O(n^2)$ 的空间。

解法2 建图优化的 $\text{Kruskal}$

方法一中，虽然使用了 $\text{Kruskal}$ 算法，但时间复杂度仍然较高，因为本题中的边数是 $O(n^2)$ 的，所以我们需要想办法将减少边数。为此，我们提出几个结论：

结论一：对于图中的任意三点 $A, B, C$ ，假设边 $A B, A C, BC$ 中 $A B$ 为最长边，那么最终答案中必然不包含边 $A B$ 。

我们利用反证法证明：假设最后答案中包含 $A B$ ，那么此时 $A C$ 与 $BC$ 两边中至少有一条边是没有被选用的，我们总可以在保证连通性的情况下，将 $A B$ 边替换为 $A C$ 与 $BC$ 两边中的某一个，使最小生成树的总权值变得更小。

结论二：对于下图中同属同一个区块的任意两点 $B, C$ ， $A$ 为原点，那么 $BC$ 不可能为三边中最长边。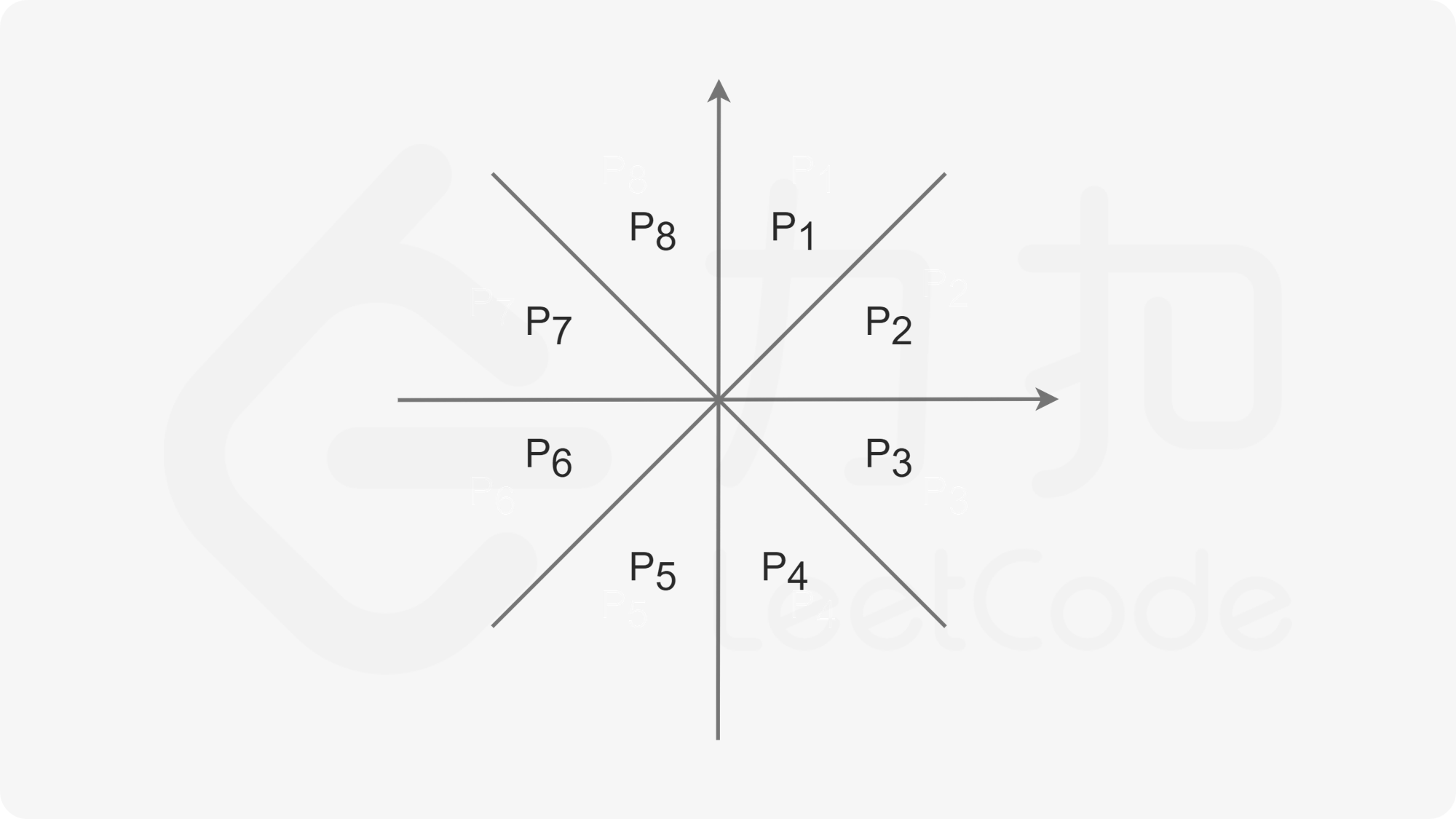

图中任意一个区块的两分割线的夹角均为 $45^\circ$ 。我们以 $P 1$ 区块为例，假设 $B(x_B,y_B),C(x_C,y_C)$ ，不失一般性，假设 $x_B + y_B \leq x_C + y_C$ 。

因为处于 $P 1$ 区域，所以有 $\leq x_B \leq y_B$ ， $\leq x_C \leq y_C$ 。所以 $BC = |x_B - x_C| + |y_B - y_C|$ 。下面我们尝试分类讨论：

当 $x_B > x_C, y_B > y_C$ ，这与 $x_B + y_B \leq x_C + y_C$ 矛盾。
当 $x_B \leq x_C, y_B > y_C$ ，此时有 $BC| = x_C - x_B + y_B - y_C$ ， $x_C + y_C - x_C + x_B - y_B + y_C = x_B - y_B + 2 \times y_C$ 。由前面各种关系可得 $y_B > y_C > x_C > x_B$ 。假设 $∣ A C ∣ < ∣ BC ∣$ ，即 $y_B > 2 \times y_C + x_B$ ，那么 $x_B + y_B > 2 \times x_B + 2 \times y_C$ ， $x_C + y_C < 2 \times y_C < |AB|$ 与前提矛盾，故 $\geq |BC|$ ；
$x_B> x_C$ 且 $y_B \leq y_c$ 。与 2 同理；
$x_B \leq x_C$ 且 $y_B \leq y_C$ 。此时显然有 $∣ A B ∣ + ∣ BC ∣ = ∣ A C ∣$ ，即有 $∣ A C ∣ > ∣ BC ∣$ 。

综上有 $\geq |BC|$ ，这个性质可以从 $P 1$ 区域推导到其他七个区域。

结论三：假设存在一点 $A$ 在原点处，那么对于图中的任意一个 $45^\circ$ 区域，我们都至多只选择其中的一个点与 $A$ 相连，且该点必然为该区域中距离 $A$ 最近的点。

我们首先利用反证法证明：假设最后答案中包含 $A B$ 与 $A C$ ，且 $B$ 与 $C$ 均位于同一个 $45^\circ$ 区域中。那么由结论二可知， $BC$ 必不为三边中的最长边。即最长边必然为 $A B$ 或 $A C$ 。由结论一可知， $A B$ 与 $A C$ 中必然有一个不包含在答案中，这与假设相悖，因此我们最多仅会选择一个点与 $A$ 相连。

我们进一步思考，既然最多仅会选择一个点与 $A$ 相连，且三边中的最长边不为 $A$ 的对边，那么仅有距离 $A$ 最近的点与 $A$ 所连的边可能出现在答案中。证毕。

依据结论三我们可以知道，一个点至多连八条边，因此我们至多只需要连出 $O (n)$ 条边。

细节：为防止重复连边，我们对每一个点只考虑对 $P 1, P 2, P 3, P 4$ 连边的情况，假设 $A$ 点坐标为 $(x, y)$ ，对于这四个点，我们可以概括为：

对于 $P 1$ 区域的 $x_1,y_1)$ ，有 $x_1 \geq x, y_1 - x_1 \geq y - x$ ，其中最近点的 $x_1 + y_1$ 最小。
对于 $P 2$ 区域的 $x_2,y_2)$ ，有 $y_2 \geq y, y_2 - x_2 \leq y - x$ ，其中最近点的 $x_2 + y_2$ 最小。
对于 $P 3$ 区域的 $x_3,y_3)$ ，有 $y_3 \leq y, y_3 + x_3 \geq y + x$ ，其中最近点的 $y_3 - x_3$ 最小。
对于 $P 4$ 区域的 $x_4,y_4)$ ，有 $x_4 \geq x, y_4 + x_4 \leq y + x$ ，其中最近点的 $y_4 - x_4$ 最小。

这样，我们分别处理每一个区域即可，以 $P 1$ 区域为例，我们先通过排序使得所有点按照横坐标从大到小排列，然后将每一个点的 $y_i - x_i$ 信息记录，将离散化后记录在数组的下标为 $y_i - x_i$ 的位置中，并利用树状数组维护该数组的前缀最小值。这样我们就可以动态地、单次 $O(\log n)$ 地计算每个点的 $P 1$ 区域所选择的点。

为了提升编码效率，实际代码中我们只实现了 $P 1$ 区域的算法，对于其它三个区域，我们通过巧妙的坐标变化使其条件变为 $P 1$ 区域，使得代码能够更加高效地复用。

class DisjointSetUnion {
private:
    vector<int> f, rank;
    int n;

public:
    DisjointSetUnion(int _n) {
        n = _n;
        rank.resize(n, 1);
        f.resize(n);
        for (int i = 0; i < n; i++) {
            f[i] = i;
        }
    }

    int find(int x) {
        return f[x] == x ? x : f[x] = find(f[x]);
    }

    int unionSet(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) {
            return false;
        }
        if (rank[fx] < rank[fy]) {
            swap(fx, fy);
        }
        rank[fx] += rank[fy];
        f[fy] = fx;
        return true;
    }
};

class BIT {
public:
    vector<int> tree, idRec;
    int n;

    BIT(int _n) {
        n = _n;
        tree.resize(n, INT_MAX);
        idRec.resize(n, -1);
    }

    int lowbit(int k) {
        return k & (-k);
    }

    void update(int pos, int val, int id) {
        while (pos > 0) {
            if (tree[pos] > val) {
                tree[pos] = val;
                idRec[pos] = id;
            }
            pos -= lowbit(pos);
        }
    }

    int query(int pos) {
        int minval = INT_MAX;
        int j = -1;
        while (pos < n) {
            if (minval > tree[pos]) {
                minval = tree[pos];
                j = idRec[pos];
            }
            pos += lowbit(pos);
        }
        return j;
    }
};

struct Edge {
    int len, x, y;
    Edge(int len, int x, int y) : len(len), x(x), y(y) {
    }
    bool operator<(const Edge& a) const {
        return len < a.len;
    }
};

struct Pos {
    int id, x, y;
    bool operator<(const Pos& a) const {
        return x == a.x ? y < a.y : x < a.x;
    }
};

class Solution {
public:
    vector<Edge> edges;
    vector<Pos> pos;

    void build(int n) {
        sort(pos.begin(), pos.end());
        vector<int> a(n), b(n);
        for (int i = 0; i < n; i++) {
            a[i] = pos[i].y - pos[i].x;
            b[i] = pos[i].y - pos[i].x;
        }
        sort(b.begin(), b.end());
        b.erase(unique(b.begin(), b.end()), b.end());
        int num = b.size();
        BIT bit(num + 1);
        for (int i = n - 1; i >= 0; i--) {
            int poss = lower_bound(b.begin(), b.end(), a[i]) - b.begin() + 1;
            int j = bit.query(poss);
            if (j != -1) {
                int dis = abs(pos[i].x - pos[j].x) + abs(pos[i].y - pos[j].y);
                edges.emplace_back(dis, pos[i].id, pos[j].id);
            }
            bit.update(poss, pos[i].x + pos[i].y, i);
        }
    }

    void solve(vector<vector<int>>& points, int n) {
        pos.resize(n);
        for (int i = 0; i < n; i++) {
            pos[i].x = points[i][0];
            pos[i].y = points[i][1];
            pos[i].id = i;
        }
        build(n);
        for (int i = 0; i < n; i++) {
            swap(pos[i].x, pos[i].y);
        }
        build(n);
        for (int i = 0; i < n; i++) {
            pos[i].x = -pos[i].x;
        }
        build(n);
        for (int i = 0; i < n; i++) {
            swap(pos[i].x, pos[i].y);
        }
        build(n);
    }

    int minCostConnectPoints(vector<vector<int>>& points) {
        int n = points.size();
        solve(points, n);

        DisjointSetUnion dsu(n);
        sort(edges.begin(), edges.end());
        int ret = 0, num = 1;
        for (auto& [len, x, y] : edges) {
            if (dsu.unionSet(x, y)) {
                ret += len;
                num++;
                if (num == n) {
                    break;
                }
            }
        }
        return ret;
    }
};

复杂度分析：

时间复杂度： $O(n\log n)$ ，其中 $O (n)$ 是节点数。预处理建边的时间复杂度为 $O(n\log n)$ ，因为需要排序，以及使用树状数组维护。在只有 $O (n)$ 条边的情况下， $\text{Kruskal}$ 的时间复杂度为 $O(n\log n)$ ，因此总时间复杂度为 $O(n\log n)$ 。
空间复杂度： $O (n)$ ，其中 $O (n)$ 是节点数。树状数组，并查集、离散化以及边集数组都只使用 $O (n)$ 的空间。
加粗样式