二叉搜索树经典笔试题【力扣、牛客】

news2024/10/6 6:45:57

文章目录

  • 1.根据二叉树创建字符串
  • 2. 二叉树的层序遍历
  • 3.二叉树的层序遍历Ⅱ
  • 4.二叉树的最近公共祖先
    • 1.法一：定位p、q在左还是右 分类讨论
    • 2.法二：利用stack求出p、q路径 求相交值
  • 5.二叉搜索树与双向链表
    • 1.法一：递归：递归过程修正指针指向
    • 2.数组：将二叉搜索树进行中序遍历可以得到由小到大的顺序排列
  • 6.前序中序遍历序列构造二叉树
  • 7.中序后序遍历序列构造二叉树
  • 8.二叉树的前序遍历【非递归】
  • 9.二叉树的中序遍历【非递归】
  • 10.二叉树的后序遍历【非递归】
    • 1.法一：栈模拟实现递归
    • 2.法二：前序遍历修改

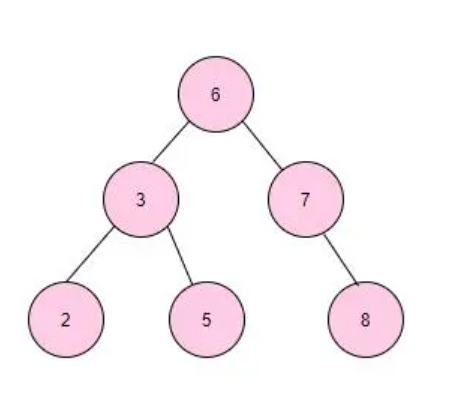
在这里插入图片描述

1.根据二叉树创建字符串

根据二叉树创建字符串在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

struct TreeNode
{
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode()
		: val(0)
		, left(nullptr)
		, right(nullptr)
	{

	}
	TreeNode(int x)
		: val(x)
		, left(nullptr)
		, right(nullptr)
	{

	}
	TreeNode(int x, TreeNode* eft, TreeNode* right)
		: val(x)
		, left(left)
		, right(right)
	{

	}
};




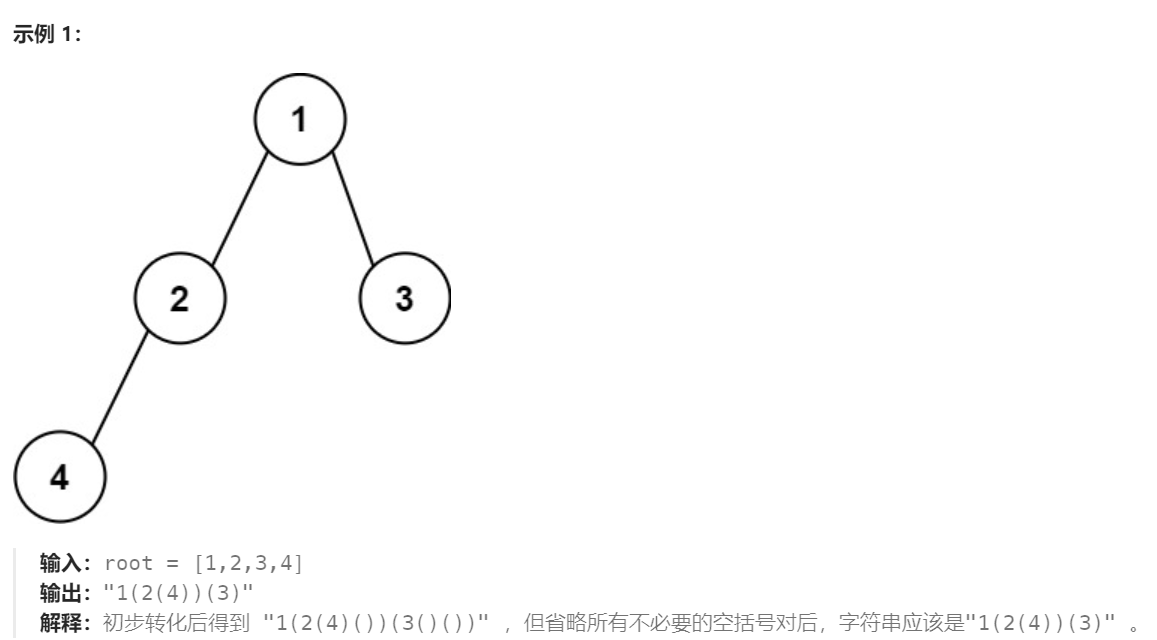
//图一分析：
//左不空 (左递归直至遇空返回上一层) 
//然后在当层判断右子树 
//右空 (返回上层 + )
//右不空 (左递归直至遇空返回上一层)
//然后在当层判断右子树 
//右空 (返回上一层 + )

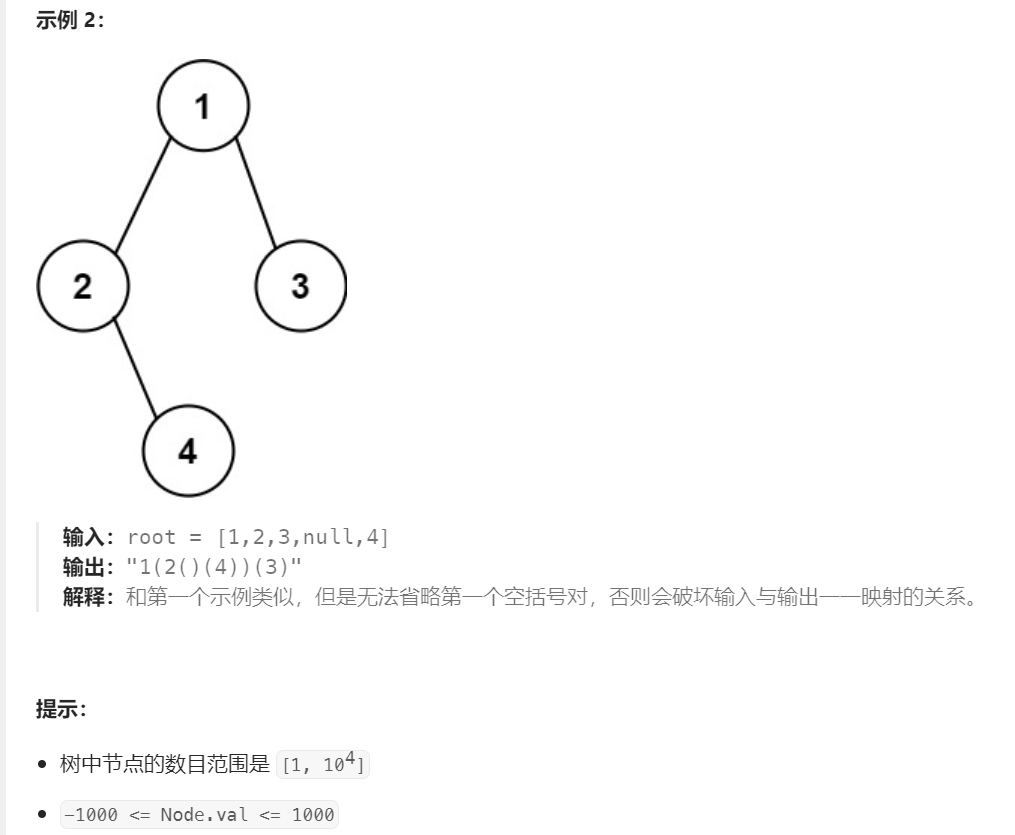
//图二分析：
//左不空 (左递归直至遇空返回上一层) 
//然后在当层判断右子树 
//右不空 (左递归直至遇空返回上一层)
//然后在当层判断右子树 
//右空 (返回上层 + )
//右不空 (左递归直至遇空返回上一层)

//左不空 右空  --省略
// 左空时第一个if两个条件才判断完
//左空   右空  --省略
//左空  右不空 --不省略
class Solution
{
public:
	string tree2str(TreeNode* root)
	{
		if (root == nullptr)
			return "";
		string str = to_string(root->val);
		//遍历完根后遍历左 遍历左的前提是左不空 如果左空看看右空不空
		//如果右也空没必要遍历 return
		//如果右不空 正常遍历
		if (root->left || root->right)
		{
			str += '(';
			str += tree2str(root->left);
			str += ')';
		}
		if (root->right) //遍历完左后遍历右 遍历右的前提是右不空 //右不空 正常遍历 右空 【看注释知右空的一律省略 直接return】
		{
			str += '(';
			str += tree2str(root->right);
			str += ')';
		}
		return str;
	}
};

2. 二叉树的层序遍历

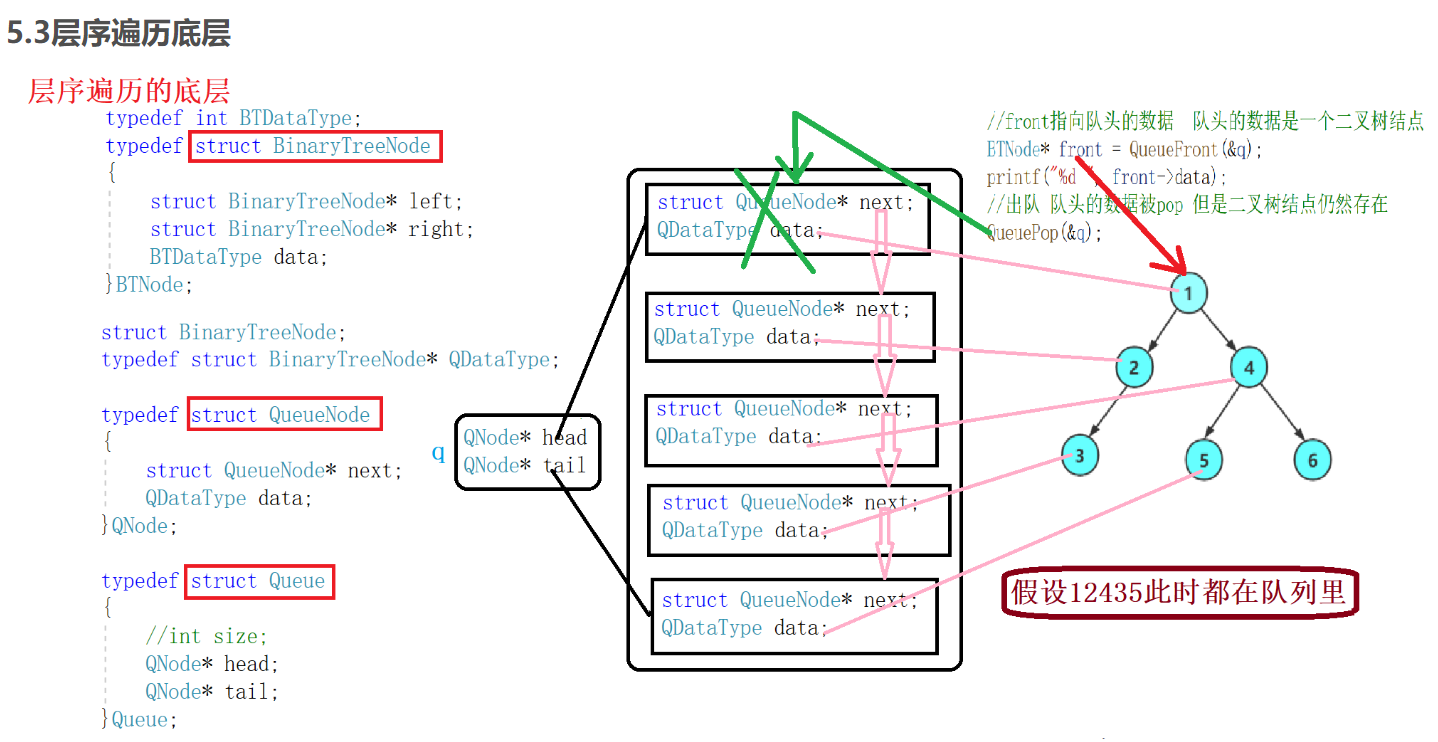
二叉树的层序遍历
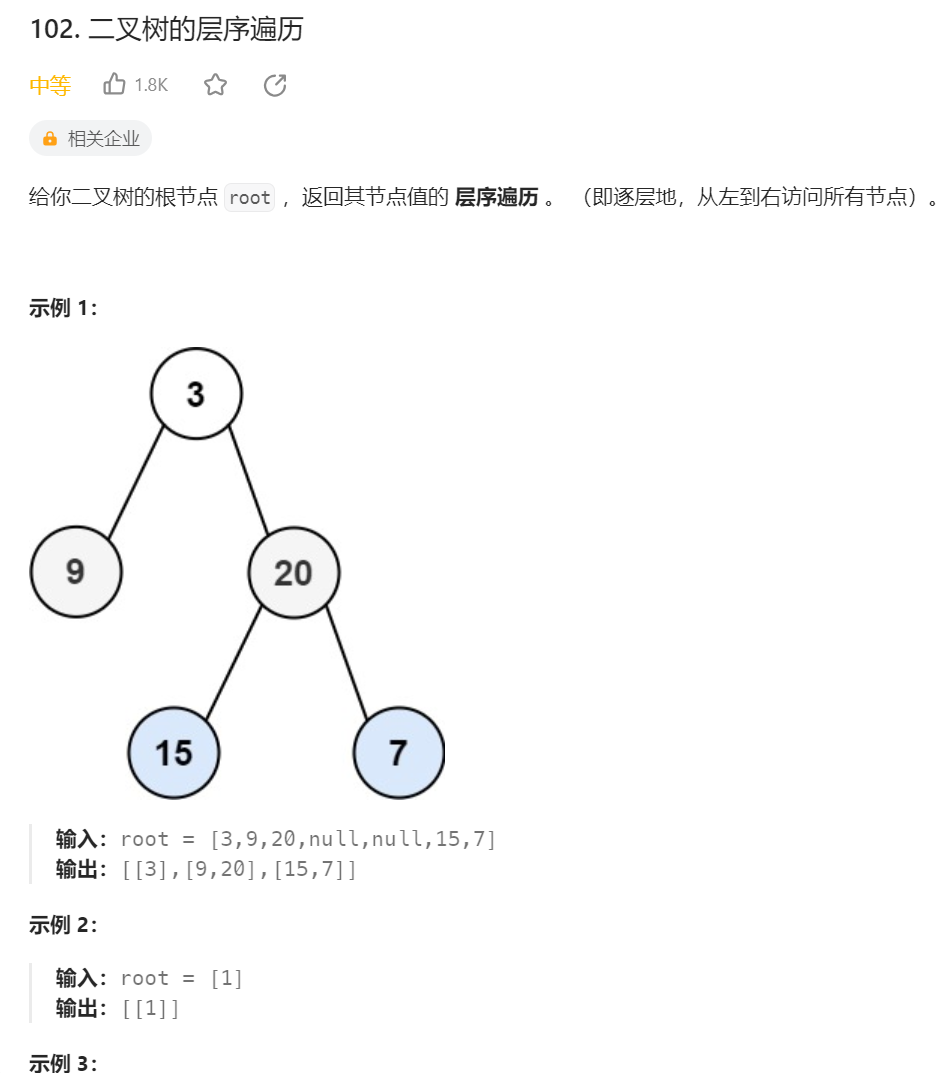
在这里插入图片描述
在这里插入图片描述
点击 二叉树【C】 查看上篇博客中的层序遍历
在这里插入图片描述

struct TreeNode
{
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode()
		: val(0)
		, left(nullptr)
		, right(nullptr)
	{

	}
	TreeNode(int x)
		: val(x)
		, left(nullptr)
		, right(nullptr)
	{

	}
	TreeNode(int x, TreeNode* eft, TreeNode* right)
		: val(x)
		, left(left)
		, right(right)
	{

	}
};


class Solution 
{
public:
	vector<vector<int>> levelorder(TreeNode* root) 
	{
		queue<TreeNode*> q;
		int LevelNodeCount = 0;
		if (root)
		{
			q.push(root);
			LevelNodeCount = 1;
		}
		vector<vector<int>> vv;
		while (!q.empty())
		{
			vector<int> v;
			while (LevelNodeCount--)
			{
				TreeNode* front = q.front();
				q.pop();
				v.push_back(front->val);

				if (front->left)
					q.push(front->left);
				if (front->right)
					q.push(front->right);
			}
			vv.push_back(v);
			
			LevelNodeCount = q.size();
		}
		return vv;
	}
};

3.二叉树的层序遍历Ⅱ

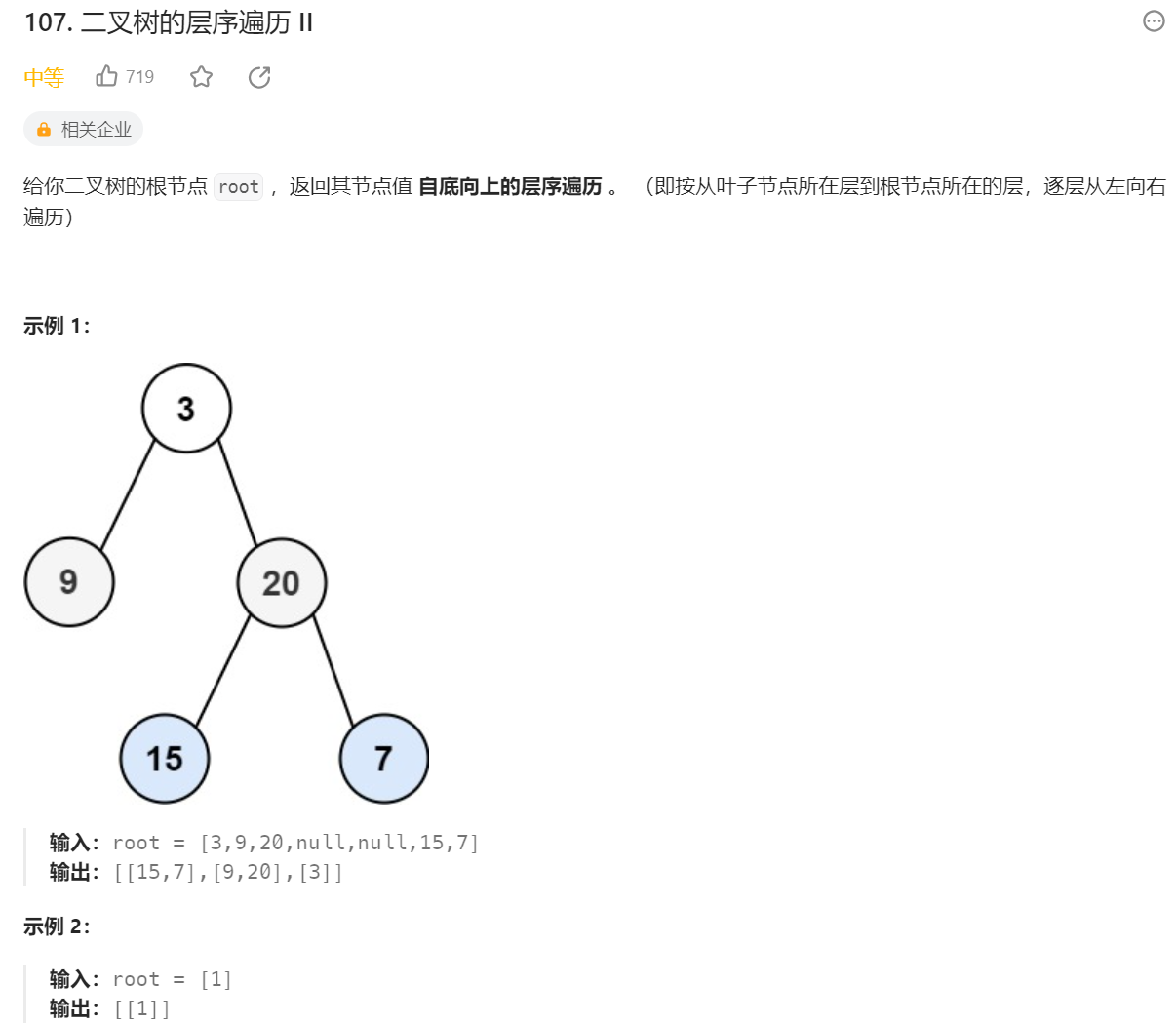
二叉树的层序遍历Ⅱ
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

class Solution 
{
public:
	vector<vector<int>> levelorder(TreeNode* root) 
	{
		queue<TreeNode*> q;
		int LevelNodeCount = 0;
		if (root)
		{
			q.push(root);
			LevelNodeCount = 1;
		}
		vector<vector<int>> vv;
		while (!q.empty())
		{
			vector<int> v;
			while (LevelNodeCount--)
			{
				TreeNode* front = q.front();
				q.pop();
				v.push_back(front->val);

				if (front->left)
					q.push(front->left);
				if (front->right)
					q.push(front->right);
			}
			vv.push_back(v);
			
			LevelNodeCount = q.size();
		}
		reverse(vv.begin(), vv.end());
		return vv;
	}
};

4.二叉树的最近公共祖先

二叉树的最近公共祖先
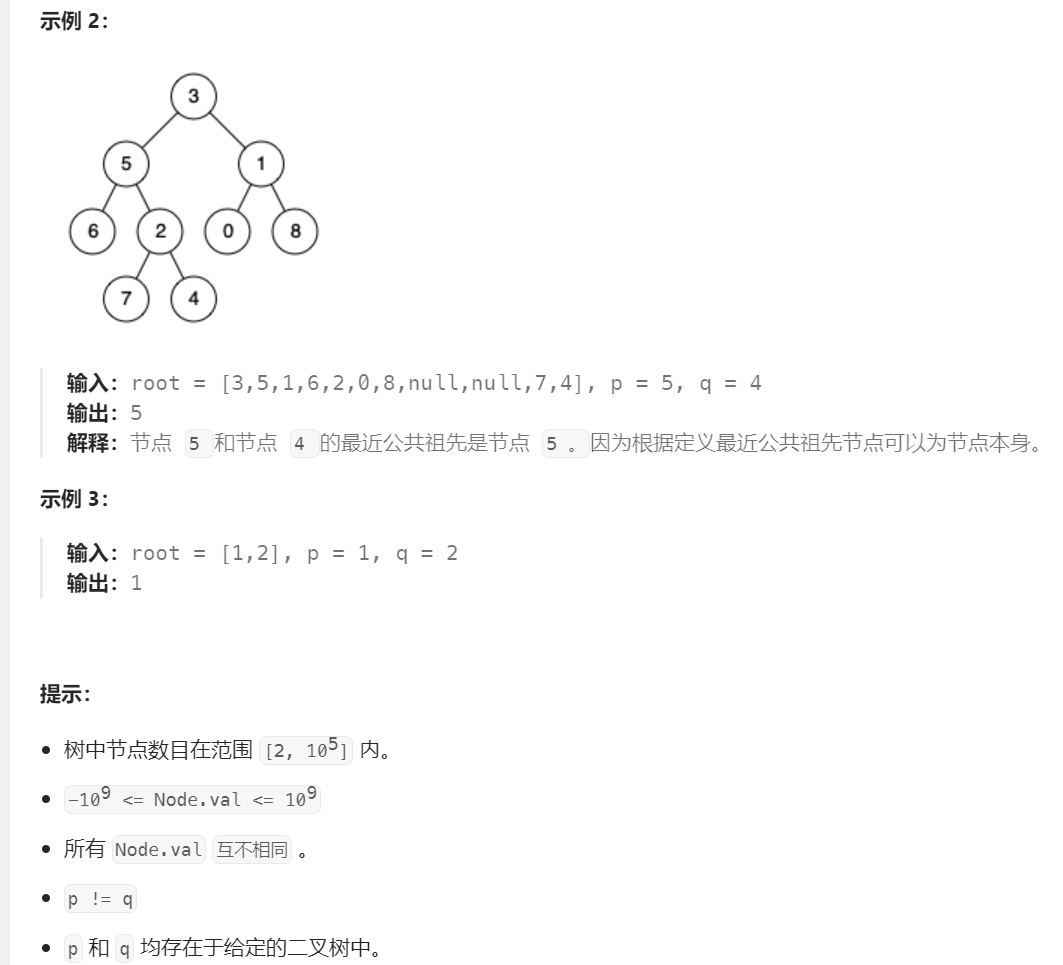
在这里插入图片描述在这里插入图片描述

1.法一：定位p、q在左还是右 分类讨论

T(N)=O(N^2)
最坏情况：树为单链即均在左侧或右侧，p、q均在单侧的底部
判断p、q的左右侧时 n-2 n-1
假设p、q均在左侧 接下来递归到左子树 继续判断p、q中是否为根？在左？在右？n-3 n-2 …

class Solution 
{
public:
	bool IsInTree(TreeNode* root, TreeNode* x)
	{
		if (root == nullptr)
			return false;

		return root == x
			|| IsInTree(root->left, x)
			|| IsInTree(root->right,x);
	}
	//求p、q的最近公共祖先
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
	{
		if (root == nullptr)
			return nullptr;
		//p、q其中一个是根 那么根就为obj
		if (root == p || root == q)
			return root;
		//判断p、q在左 ？右
		bool pInLeft = IsInTree(root->left, p);
		bool pInRight = !pInLeft;
		bool qInLeft = IsInTree(root->left, q);
		bool qInRight = !qInLeft;

		//一左一右==》root为obj
		if ((pInLeft && qInRight) || (pInRight && qInLeft))
			return root;
		//均左==》递归到左子树
		if (pInLeft && qInLeft)
			return lowestCommonAncestor(root->left, p, q);
		//均右==》递归到右子树
		else
			return lowestCommonAncestor(root->right, p, q);
	}
};

2.法二：利用stack求出p、q路径 求相交值

class Solution
{
public:
	bool GetPath(TreeNode* root, TreeNode* pobj, stack<TreeNode*>& route)
	{
		if (root == nullptr)
			return false;
		route.push(root);
		if (root == pobj)
			return true;
		if (GetPath(root->left, pobj, route))
			return true;
		if (GetPath(root->right, pobj, route))
			return true;
		route.pop();
		return false;
	}

	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
	{
		stack<TreeNode*> pRoute;
		stack<TreeNode*> qRoute;
		GetPath(root, p, pRoute);
		GetPath(root, q, qRoute);
		//找路径相遇点
		while (pRoute.size() != qRoute.size())
		{
			if (pRoute.size() > qRoute.size())
				pRoute.pop();
			else
				qRoute.pop();
		}
		while (pRoute.top() != qRoute.top())
		{
			pRoute.pop();
			qRoute.pop();
		}
		return pRoute.top();
	}
};

5.二叉搜索树与双向链表

二叉搜索树与双向链表
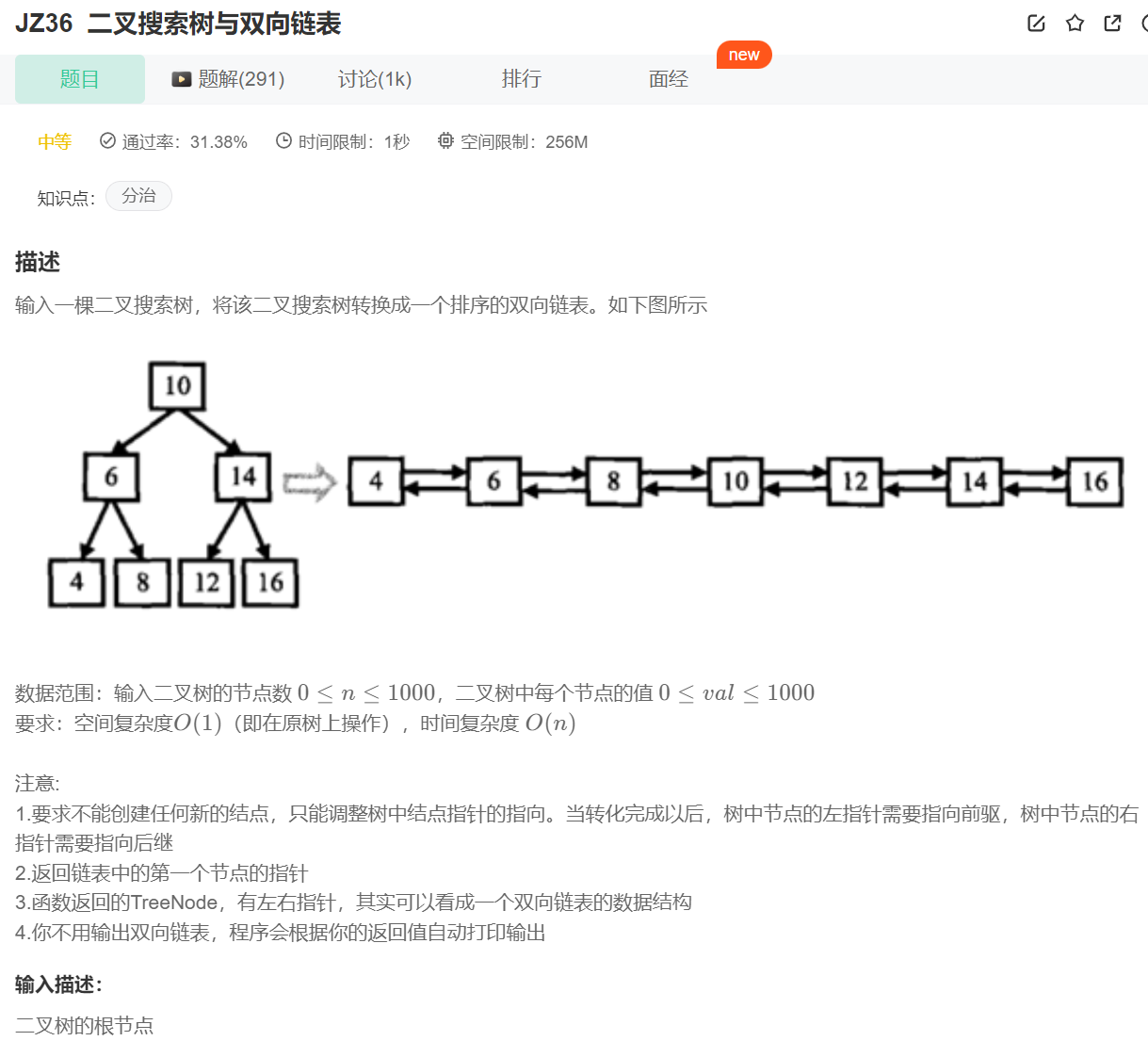
在这里插入图片描述
在这里插入图片描述

1.法一：递归：递归过程修正指针指向

class Solution
{
public: 
    //中序遍历
	void InOrderConvert(TreeNode* cp, TreeNode*& prv)
	{
		if (cp == nullptr)
			return;
		
		InOrderConvert(cp->left, prv);//一路向左 遇空返回上一层
		//前左指向前驱
		cp->left = prv;//left==prv即left指向prv所指向的结点
		//前驱非空 前结点的right指向后面那个结点
		if (prv)
			prv->right = cp;
		//更新prv
		prv = cp;
		//一路向右 遇空返回上一层
		InOrderConvert(cp->right, prv);
	}//==》当前层函数结束 返回上一层
	TreeNode* Convert(TreeNode* pRootOfTree)
	{
		TreeNode* prev = nullptr;

		InOrderConvert(pRootOfTree, prev);

		TreeNode* head = pRootOfTree;
		//当传一颗空树 head在此就发挥了作用
		while (head && head->left)
			head = head->left;
		return head;
	}
};

2.数组：将二叉搜索树进行中序遍历可以得到由小到大的顺序排列

/*
struct TreeNode
{
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) 
	:val(x)
	, left(NULL)
	, right(NULL) 
	{

	}
};
*/

class Solution 
{
public:
	vector<TreeNode*> v;

	void inorder(TreeNode* root) 
	{
		if (!root) return;

		inorder(root->left);
		v.push_back(root);
		inorder(root->right);
	}


	TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		if (!pRootOfTree) 
			return pRootOfTree;
		inorder(pRootOfTree);
		for (int i = 0; i < v.size() - 1; i++) 
		{ 
			v[i]->right = v[i + 1];
			v[i + 1]->left = v[i];
		}
		return v[0];
	}

};

6.前序中序遍历序列构造二叉树

前序中序遍历序列构造二叉树
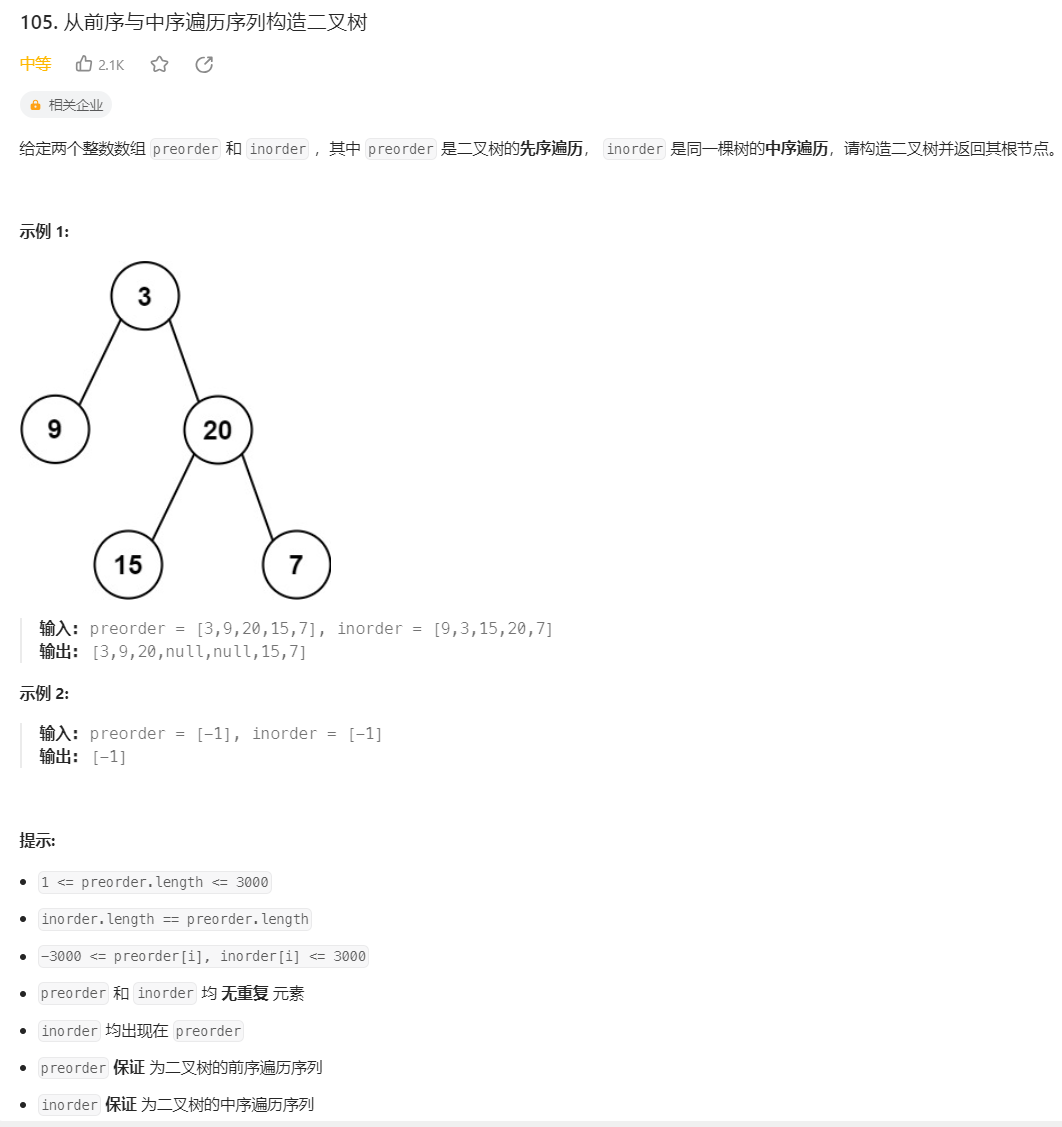
在这里插入图片描述

class Solution 
{
public:
	TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& i, int begin, int end)
	{
		if (begin > end) 
			return nullptr;
	   
		//遍历inorder 定位到根节点
		//[begin, x - 1] x [x + 1, end]
		int x = begin;
		for (x = begin; x <= end; ++x)
		{
			if (inorder[x] == preorder[i])
				break;
		}

		TreeNode* root = new TreeNode(preorder[i++]);
		
		root->left = _buildTree(preorder, inorder, i, begin, x - 1);
		root->right = _buildTree(preorder, inorder, i, x + 1, end);
		return root;
	};

	TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
	{
		int index = 0;//前序遍历数组第一个元素即根节点
		return _buildTree(preorder, inorder, index, 0, inorder.size() - 1);
	}
};

7.中序后序遍历序列构造二叉树

中序后序遍历序列构造二叉树
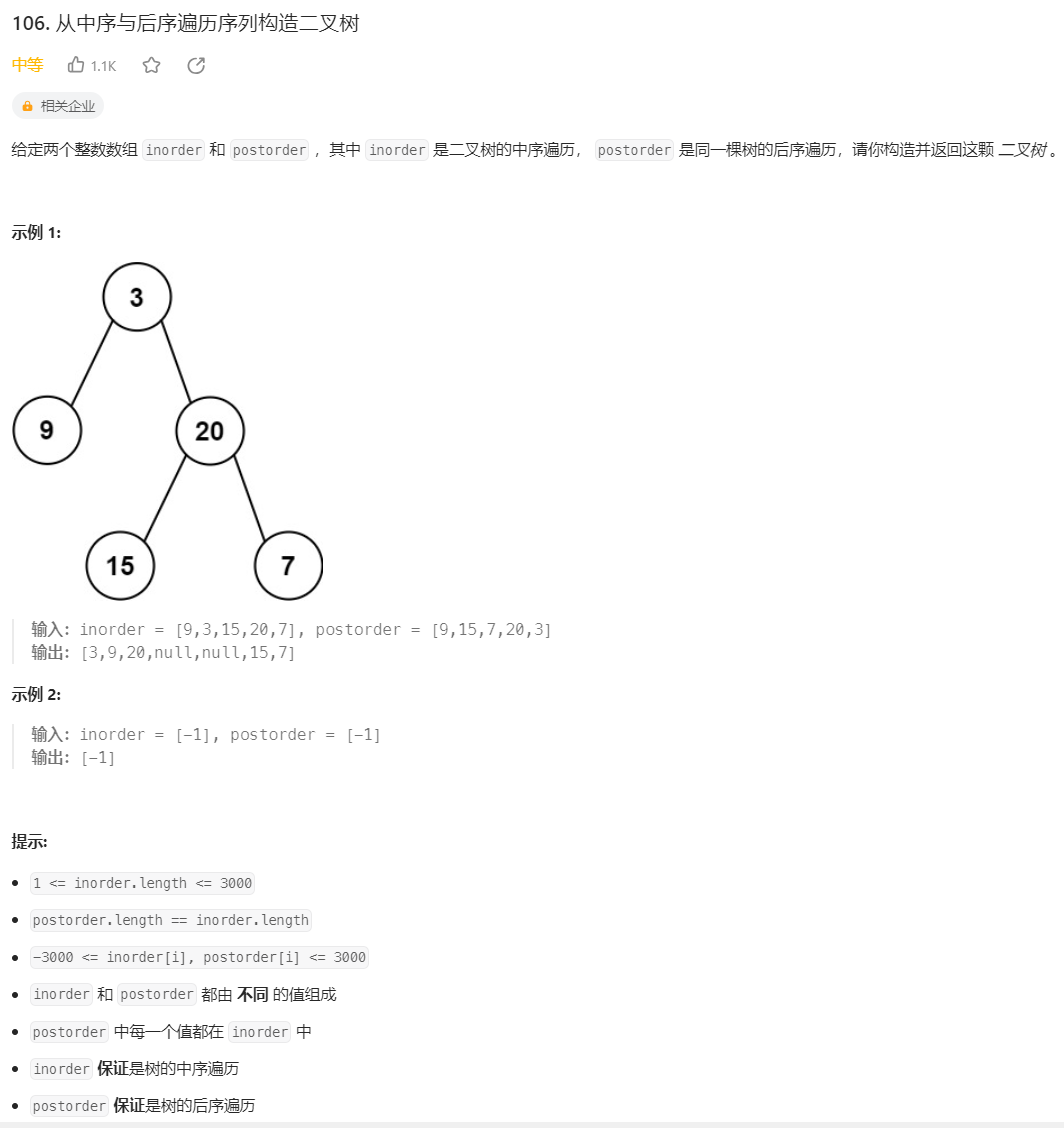
在这里插入图片描述

class Solution 
{
public:
	TreeNode* _buidTree(vector<int>& inorder, vector<int>& postorder, int& i,  int begin, int end)
	{
		if (begin > end) 
			return nullptr;
		
		int x = begin;
		for (x = begin; x <= end; ++x)
		{
			if (inorder[x] == postorder[i])
				break;
		}
        TreeNode* root = new TreeNode(postorder[i--]);

		root->right = _buidTree(inorder, postorder, i, x + 1, end);
		root->left = _buidTree(inorder, postorder, i, begin, x - 1);
		return root;
	}

	TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
	{
		int index = postorder.size() - 1;
		return _buidTree(inorder, postorder, index, 0, inorder.size() - 1);
	}
};

8.二叉树的前序遍历【非递归】

二叉树的前序遍历
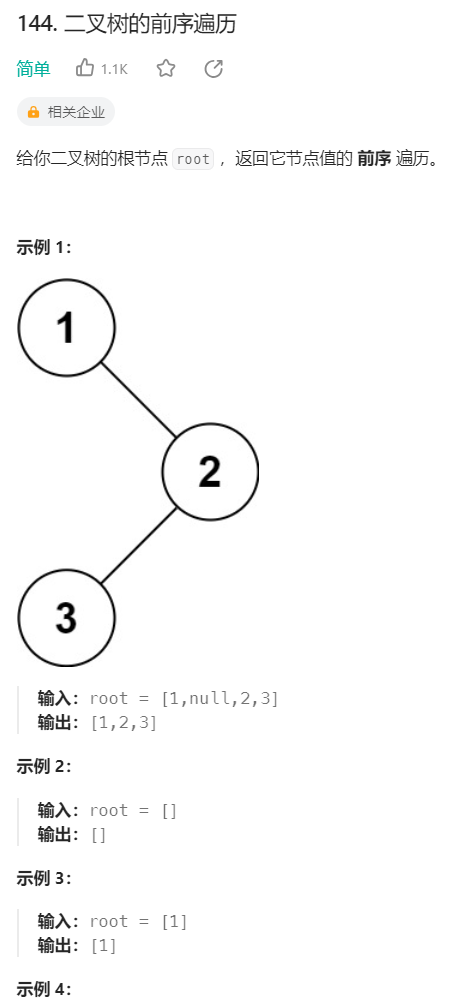
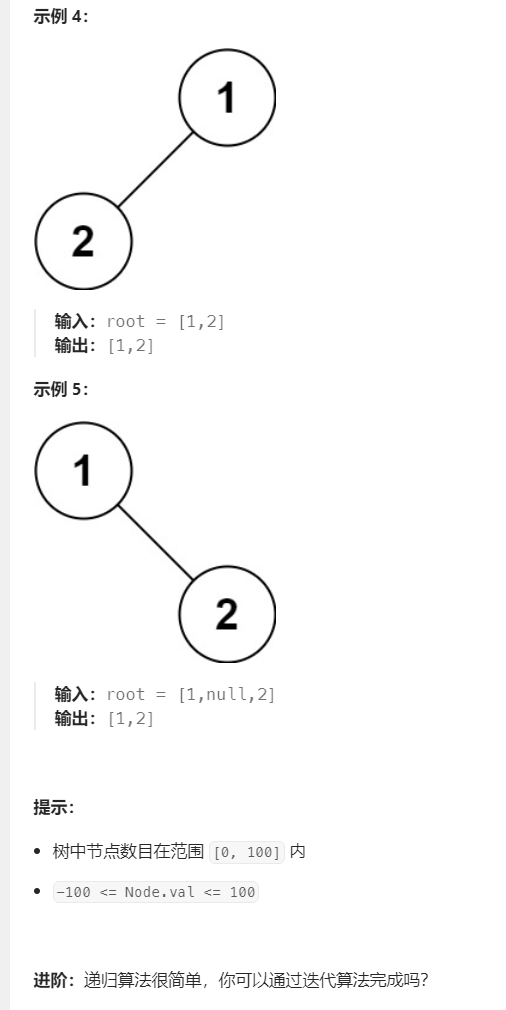
在这里插入图片描述
在这里插入图片描述

vector<int> preorderTraversal(TreeNode* root)
{
	vector<int> v;       //v存储遍历的数据
	stack<TreeNode*> st; //利用栈的特点 调整读取数据的顺序存入到v中
	TreeNode* cp = root;
	while (cp || !st.empty())
	{
		//左路结点
		while (cp)
		{
			v.push_back(cp->val);
			st.push(cp);
			cp = cp->left;
		}
		//左路结点的右子树
		TreeNode* top = st.top();
		cp = top->right;
		st.pop();
	}
	return v;
}

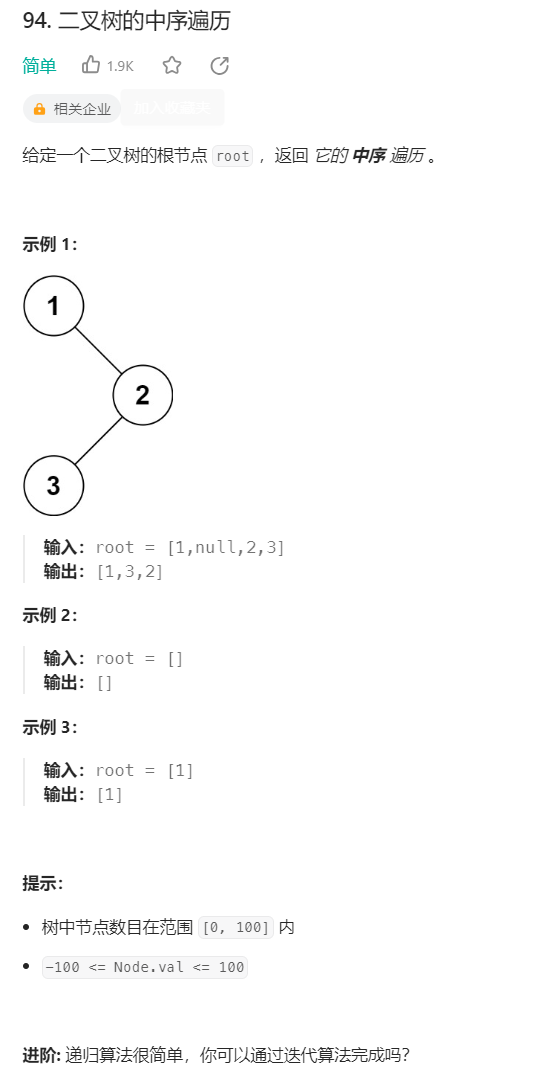
9.二叉树的中序遍历【非递归】

二叉树的中序遍历
在这里插入图片描述

vector<int> inorderTraversal(TreeNode* root) 
{
	vector<int> v;
	stack<TreeNode*> st;
	TreeNode* cp = root;
	while (cp || !st.empty())   
	{
		while (cp)
		{
			st.push(cp);
			cp = cp->left;
		}

		TreeNode* top = st.top();
		v.push_back(top->val);
		cp = top->right;
		st.pop();
	}
	return v;
};

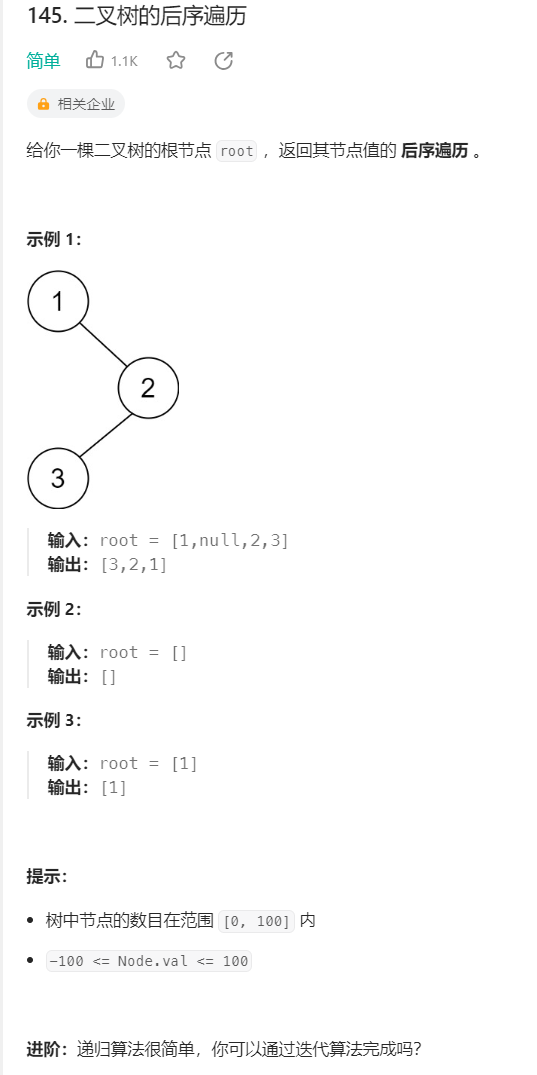
10.二叉树的后序遍历【非递归】

二叉树的后序遍历
在这里插入图片描述

1.法一：栈模拟实现递归

vector<int> postorderTraversal(TreeNode* root)
{
	vector<int> v;
	stack<TreeNode*> st;
	TreeNode* cp = root;
	TreeNode* prv = nullptr;
	while (cp || !st.empty())
	{
		while (cp)
		{
			st.push(cp);
			cp = cp->left;
		}
		TreeNode* top = st.top();
		if (top->right == nullptr || top->right == prv)
		{
			v.push_back(top->val);
			prv = top;
			st.pop();
		}
		else
		{
			cp = top->right;
		}
	}
	return v;
};

2.法二：前序遍历修改

class Solution 
{
public:
    vector<int> postorderTraversal(TreeNode* root) 
    {
		vector<int> v;
        stack<TreeNode*> st;
		
		st.push(root);
		while (!st.empty())
		{
			TreeNode* top = st.top();
			st.pop();
			if (top)
				v.push_back(top->val);
			else
				continue;
			st.push(top->left);
			st.push(top->right);
		}
        reverse(v.begin(), v.end());
        return v;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1015565.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基础篇之环境搭建

基础篇之环境搭建

文章目录 一、安装依赖包二、SDK源码包下载三、分块文件合并四、更新SDK五、可能存在的问题与解决方案5.1 contains uncommitted changes5.2 app/QLauncher: UnicodeDecodeError5.3 Cannot checkout app/QLauncher 六、软件包下载6.1 下载地址6.2 使用方法 一、安装依赖包 sud…
阅读更多...
PowerDesigner 逆向工程以及IDEA中UML插件

PowerDesigner 逆向工程以及IDEA中UML插件

1、MySQL数据库连接&#xff08;JDBC方式&#xff09; 1.1 新建一个pdm&#xff0c;dbms选择mysql 1.2 Database - Connect 选择数据库连接 1.3 配置连接信息 数据库连接这里是通过一个配置文件来获取连接信息的&#xff0c;首次的话因为没有&#xff0c;所以我们需要选择…
阅读更多...
git 推送出现fatal: The remote end hung up unexpectedly解决方案

git 推送出现fatal: The remote end hung up unexpectedly解决方案

在使用git更新或提交项目时候出现 "fatal: The remote end hung up unexpectedly " 的报错&#xff1b; 报错的原因原因是推送的文件太大。 下面给出解决方法 方法一&#xff1a; 修改提交缓存大小为500M&#xff0c;或者更大的数字 git config --global http.po…
阅读更多...
01_网络编程_传统IO

01_网络编程_传统IO

网络编程 1.什么是网络编程 在网络通信协议下&#xff0c;不同计算机上运行的程序&#xff0c;进行的数据传输。 如果想把一个计算的结果&#xff0c;或者是电脑上的文件通过网络传递给你的朋友&#xff0c;就需要用到网络编程。 在实际生活中&#xff0c;网络通信无处不在…
阅读更多...
javabasic

javabasic

计算机基础 一、学前知识 1. 计算机组成 2. 进制的概念 &#xff08;1&#xff09;二进制的存储 计算机不管是内存还是硬盘&#xff0c;都是以二进制的形式存储。如同一张巨大的表格&#xff0c;里面都是由0和1组成。 二进制&#xff1a;逢2进1 基数为2&#xff0c;数值部分…
阅读更多...
DP读书：《openEuler操作系统》（二）操作系统的发展史

DP读书：《openEuler操作系统》（二）操作系统的发展史

操作系统的发展历史 操作系统的发展历史手工操作时代批处理系统多道程序系统分时操作系统CTSSMULTICS的历史UNIX和Linux的历史Debian系列Red Hat系列 DOS和Windows的历史DOS的历史&#xff1a;Windows的历史&#xff1a; Android和iOS的历史Android&#xff1a;iOS&#xff1a;…
阅读更多...
MCU软核 3. Xilinx Artix7上运行cortex-m3软核

MCU软核 3. Xilinx Artix7上运行cortex-m3软核

0. 环境 - win10 vivado 2018.3 keil mdk - jlink - XC7A35TV12 1. 下载资料 https://keilpack.azureedge.net/pack/Keil.V2M-MPS2_DSx_BSP.1.1.0.pack https://gitee.com/whik/cortex_m3_on_xc7a100t 2. vivado 2018 Create Project -> Next -> -> Project n…
阅读更多...
web安全漏洞-SQL注入攻击实验

web安全漏洞-SQL注入攻击实验

实验目的 学习sql显注的漏洞判断原理掌握sqlmap工具的使用分析SQL注入漏洞的成因 实验工具 sqlmap是用python写的开源的测试框架&#xff0c;支持MySQL&#xff0c;Oracle&#xff0c;PostgreSQL&#xff0c;Microsoft SQL Server&#xff0c;Microsoft Access&#xff0c;I…
阅读更多...
2023微信头像生成小程序源码/基于skyline+vue3+t

2023微信头像生成小程序源码/基于skyline+vue3+t

微信头像生成小程序&#xff0c;基于skylinevue3t该项目已适配微信小程序隐私政策&#xff0c;截图、获取头像等诸多新的接口 如何使用&#xff1a; 将代码导入到HBuilderX开发工具&#xff0c;可无需修改任何代码&#xff0c;运行并编译到微信开发者工具 skyline需要使用微…
阅读更多...
C++ 的继任者：Carbon Language | 开源日报 0911

C++ 的继任者：Carbon Language | 开源日报 0911

carbon-language/carbon-lang Stars: 31.1k License: NOASSERTION Carbon Language 是一个实验性的 C 继任者项目。它旨在提供与 C 相当的性能&#xff0c;并具有低级访问位和地址的功能&#xff0c;以及与现有 C 代码进行互操作、快速可扩展构建等特点。该项目还强调了以下核…
阅读更多...
io概述及其分类

io概述及其分类

一、IO概念 • I/O 即输入Input/ 输出Output的缩写&#xff0c;其实就是计算机调度把各个存储中&#xff08;包括内存和外部存储&#xff09;的数据写入写出的过程&#xff1b; I : Input O : Output 通过IO可以完成硬盘文件的读和写。 • java中用“流&#xff08;stream&am…
阅读更多...
太牛啦！Python入门到精通 只用了3个多月

太牛啦！Python入门到精通 只用了3个多月

最近 GitHub 热榜上持续有一个这样的 Python 项目&#xff0c;自称「100天从新手到大师」。目前 Star 数量已有 19000 多。 作者在开头列出了 Python 的一些应用领域 作者的计划目录 Day01~15 - Python语言基础 Day16~20 - Python语言进阶 Day21~30 - Web前端入门 Day31~3…
阅读更多...
基于RuoYi-Flowable-Plus的ruoyi-nbcio项目的formdesigner文件上传与回显处理

基于RuoYi-Flowable-Plus的ruoyi-nbcio项目的formdesigner文件上传与回显处理

更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码&#xff1a; https://gitee.com/nbacheng/ruoyi-nbcio 本节说明ruoyi-nbcio项目的formdesigner文件上传与回显处理&#xff0c;不过目前还只实现oss的formdesigner的文件上传与回显功能。 1、前端方面 formdesigne…
阅读更多...
IDEA中Debug测试的基本使用

IDEA中Debug测试的基本使用

Debug简介 Debug是用来追踪代码&#xff0c;通常在程序运行中出现异常的时候启动debug模式可以分析定位异常发生的位置&#xff0c;以及在运行过程中参数的变化&#xff0c;通常我们也可以启动Debug模式来跟踪代码的运行流程去学习三方框架的源码 Debug与Junit的区别 Debug与JU…
阅读更多...
力扣236 补9.14

力扣236 补9.14

做不来&#xff0c;我做中等题基本上都是没有思路&#xff0c;这里需要先遍历祖先节点&#xff0c;那必然用先序遍历&#xff0c;这题还是官方题解容易理解&#xff0c;第二火的题解反而把我弄得脑袋昏昏的。 class Solution { TreeNode ans; public TreeNode lowestCommonAnce…
阅读更多...
私域流量的优势

私域流量的优势

私域流量是指由自身品牌或个人拥有并具备完全掌控权的流量资源。它相比于传统的广告推广&#xff0c;拥有独特的优势。 首先&#xff0c;私域流量能够更加精准地定位目标用户&#xff0c;实现精准传播。不再盲目投放广告&#xff0c;而是通过建立自身社群、粉丝群&#xff0c;获…
阅读更多...
Postman应用——下载注册和登录

Postman应用——下载注册和登录

文章目录 下载安装注册登录注册账号登录账号 下载安装 Postman下载&#xff1a;https://www.postman.com/ 访问链接后&#xff0c;进入首页&#xff0c;根据自己的操作系统下载对应的版本。 找到下载到的目录直接双击.exe文件&#xff0c;会默认安装在C盘&#xff0c;安装完会…
阅读更多...
使用VMware 16 安装银河麒麟V10 --九五小庞

使用VMware 16 安装银河麒麟V10 --九五小庞

1.下载 银河麒麟系统V10 服务版镜像包&#xff1a; Kylin-Server-10-SP1-Release-Build04-20200711-x86_64.iso 百度云盘链接&#xff1a;https://pan.baidu.com/s/1z0GCEadvefUA8R988qDP5Q 提取码&#xff1a;1l0g 2.运行VMware Workstation&#xff0c;创建新的虚拟机&…
阅读更多...
【动态规划刷题 15】最长定差子序列 最长的斐波那契子序列的长度

【动态规划刷题 15】最长定差子序列 最长的斐波那契子序列的长度

1218. 最长定差子序列 链接: 1218. 最长定差子序列 给你一个整数数组 arr 和一个整数 difference&#xff0c;请你找出并返回 arr 中最长等差子序列的长度&#xff0c;该子序列中相邻元素之间的差等于 difference 。 子序列 是指在不改变其余元素顺序的情况下&#xff0c;通…
阅读更多...
python程序商业化，代码安全最终方案，pyinstaller与cython打包python执行程序

python程序商业化，代码安全最终方案，pyinstaller与cython打包python执行程序

其实一般的程序安全上只需要两步就行&#xff0c;没必要再加密改解释器等&#xff0c;已经不可能反编译到原有python了&#xff0c;因为动态链接库就是汇编了&#xff0c;中间经历了python转c,c在转动态库&#xff0c;代码已经没有可读性了。但是一些密码等重要字符还是要处理好…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023