1218. 最长定差子序列
链接: 1218. 最长定差子序列
给你一个整数数组 arr 和一个整数 difference,请你找出并返回 arr 中最长等差子序列的长度,该子序列中相邻元素之间的差等于 difference 。
子序列 是指在不改变其余元素顺序的情况下,通过删除一些元素或不删除任何元素而从 arr 派生出来的序列。
示例 1:
输入:arr = [1,2,3,4], difference = 1
输出:4
解释:最长的等差子序列是 [1,2,3,4]。
示例 2:
输入:arr = [1,3,5,7], difference = 1
输出:1
解释:最长的等差子序列是任意单个元素。
示例 3:
输入:arr = [1,5,7,8,5,3,4,2,1], difference = -2
输出:4
解释:最长的等差子序列是 [7,5,3,1]。
1.状态表示*
dp[i] 表⽰:以 i 位置的元素为结尾所有的⼦序列中,最⻓的等差⼦序列的⻓度
2.状态转移方程
对于 dp[i] ,上⼀个定差⼦序列的取值定为 arr[i] - difference 。只要找到以上⼀个数字为结尾的定差⼦序列⻓度的 dp[arr[i] - difference] ,然后加上 1 ,就是以 i 为结尾的定差⼦序列的⻓度。
因此,这⾥可以选择使⽤哈希表做优化。我们可以把「元素, dp[j] 」绑定,放进哈希表中。甚⾄不⽤创建 dp 数组,直接在哈希表中做动态规划。
3. 初始化
刚开始的时候,需要把第⼀个元素放进哈希表中, hash[arr[0]] = 1
4. 填表顺序
显⽽易⻅,填表顺序「从左往右」
5. 返回值
根据「状态表⽰」,返回整个 dp 表中的最⼤值
代码:
int longestSubsequence(vector<int>& arr, int difference) {
unordered_map<int, int> hash;
hash[arr[0]] = 1;
int ret = 1;
for(int i = 1; i < arr.size(); i++)
{
hash[arr[i]] = hash[arr[i] - difference] + 1;
ret = max(ret, hash[arr[i]]);
}
return ret;
}
873. 最长的斐波那契子序列的长度
链接: 873. 最长的斐波那契子序列的长度
如果序列 X_1, X_2, …, X_n 满足下列条件,就说它是 斐波那契式 的:
n >= 3
对于所有 i + 2 <= n,都有 X_i + X_{i+1} = X_{i+2}
给定一个严格递增的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 arr 中派生出来的,它从 arr 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如, [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列)
示例 1:
输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。
示例 2:
输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,最⻓的斐波那契⼦
序列的⻓度。规定⼀下 i < j
1.状态表示*
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,最⻓的斐波那契⼦序列的⻓度。
2.状态转移方程
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = c - b 。我们根
据 a 的情况讨论:
- i. a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓斐波那契⼦序列的⻓度,然后再加上
j 位置的元素即可。于是 dp[i][j] = dp[k][i] + 1 ; - ii. a 存在,但是 b < a < c :此时只能两个元素⾃⼰玩了, dp[i][j] = 2 ;
- iii. a 不存在:此时依旧只能两个元素⾃⼰玩了, dp[i][j] = 2 。
3. 初始化
可以将表⾥⾯的值都初始化为 2 。
4. 填表顺序
a. 先固定最后⼀个数;
b. 然后枚举倒数第⼆个数。
5. 返回值
因为不知道最终结果以谁为结尾,因此返回 dp 表中的最⼤值 ret 。
但是 ret可能⼩于 3 ,⼩于 3 的话说明不存在。
因此需要判断⼀下
代码:
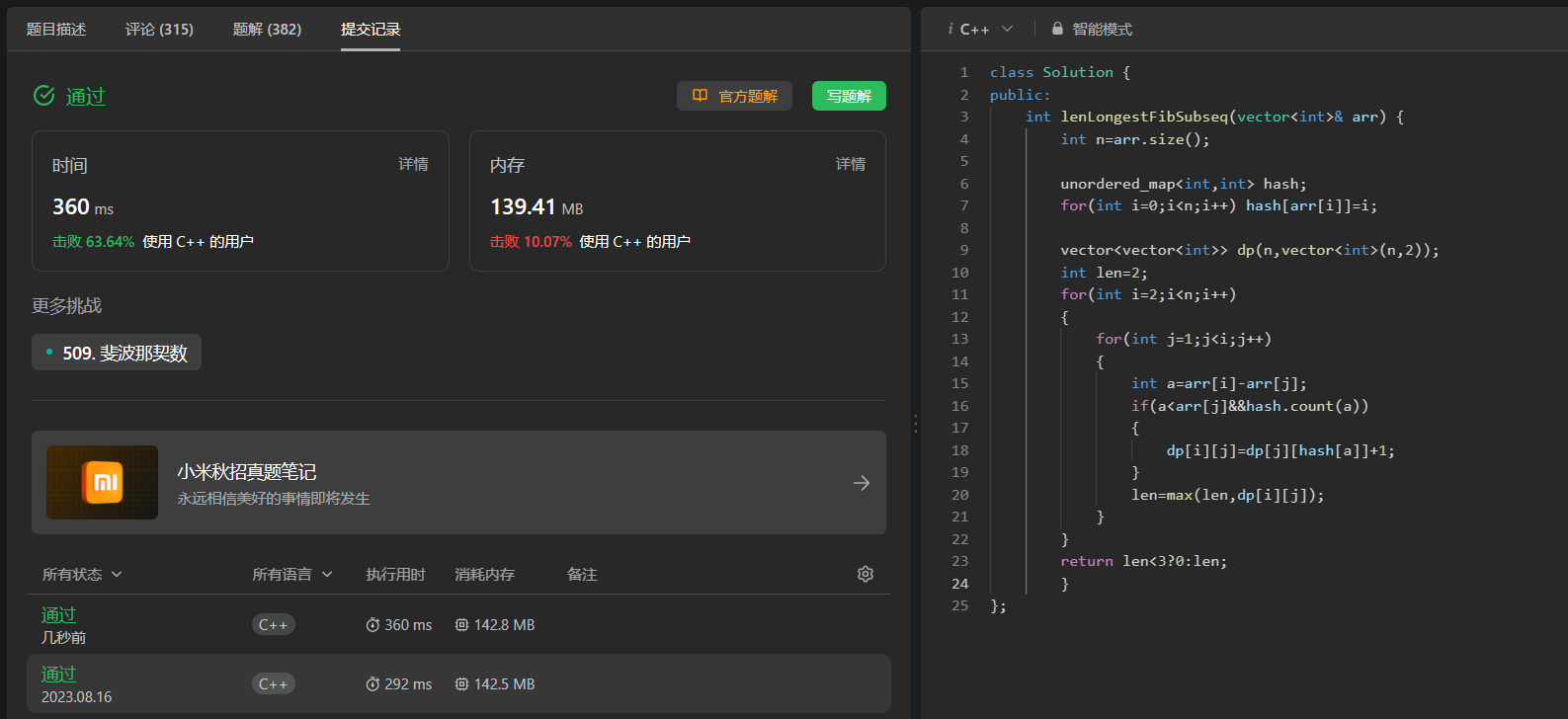
int lenLongestFibSubseq(vector<int>& arr) {
int n=arr.size();
unordered_map<int,int> hash;
for(int i=0;i<n;i++) hash[arr[i]]=i;
vector<vector<int>> dp(n,vector<int>(n,2));
int len=2;
for(int i=2;i<n;i++)
{
for(int j=1;j<i;j++)
{
int a=arr[i]-arr[j];
if(a<arr[j]&&hash.count(a))
{
dp[i][j]=dp[j][hash[a]]+1;
}
len=max(len,dp[i][j]);
}
}
return len<3?0:len;
}