在强化学习中,我们有兴趣确定一种最大化获取奖励的策略。最近我们被客户要求撰写关于MDP的研究报告,包括一些图形和统计输出。假设环境是马尔可夫决策过程 (MDP)的理想模型 ,我们可以应用动态编程方法来解决强化学习问题。
在这篇文章中,我介绍了可以在MDP上下文中使用的三种动态编程算法。为了使这些概念更容易理解,我在网格世界的上下文中实现了算法,这是演示强化学习的流行示例。
相关视频:马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例
马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例
,时长07:25
相关视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
,时长08:47
在开始使用该应用程序之前,我想快速提供网格世界上后续工作所需的理论背景。
MDP的关键强化学习术语
以下各节解释了强化学习的关键术语,即:
- 策略: 代理应在哪种状态下执行哪些操作
- 状态值函数: 每个州关于未来奖励的期望值
- 行动价值函数: 在特定状态下针对未来奖励执行特定行动的预期价值
- 过渡概率: 从一种状态过渡到另一种状态的概率
- 奖励功能: 代理在状态之间转换时获得的奖励
状态值函数
给定策略ππ,状态值函数Vπ(s)Vπ(s)将每个状态ss映射到代理在此状态下可获得的预期收益:
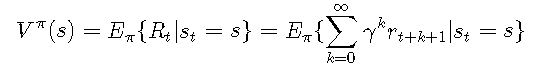
式中,stst表示时刻tt的状态。参数γ∈[0,1]γ∈[0,1]称为 折扣因子。它决定了未来奖励的影响。
动作值函数
给定策略ππ,动作值函数Qπ(s,a)Qπ(s,a)确定在状态ss中执行动作aa时的预期奖励:
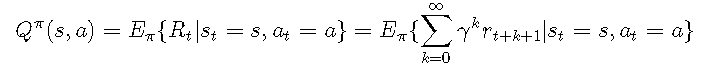
转移概率
在状态ss中执行动作aa可以将代理转换为状态s's'。通过Pass'Pss'a描述发生此过渡的可能性。
奖励函数
奖励函数Rass'Rss'a指定当代理通过动作aa从状态ss过渡到状态s's'时获得的奖励。
Gridworld中的三种基本MDP算法的演示
在本文中,您将学习如何在网格世界中为MDP应用三种算法:
- 策略评估: 给定策略ππ,与ππ相关的价值函数是什么?
- 策略迭代: 给定策略ππ,我们如何找到最佳策略π∗π∗?
- 值迭代: 如何从头开始找到最佳策略π∗π∗?
在gridworld中,代理的目标是到达网格中的指定位置。该代理可以向北,向东,向南或向西移动。这些动作由集合{N,E,S,W} {N,E,S,W}表示。请注意,代理始终知道状态(即其在网格中的位置)。
网格中存在一些壁,代理无法通过这些壁。
基本的Gridworld实施
我已经以面向对象的方式实现了gridworld。以下各节描述了我如何设计地图和策略实体的代码。
Gridworld地图
为了实现gridworld,我首先要做的是代表地图的类。我定义了以下格式来表示各个网格单元:
#指示墙壁X表明目标- 空白表示空块
依靠这些符号, 构造 了下面的map :
###################
# X#
# ########### #
# # # #
# # ####### # #
# # # # # #
# # # # #
# # #
# #
### ###
# #
###################
我实现了 MapParser,它生成一个 Map对象。地图对象控制 对gridworld 单元的访问。单个单元格子类定义特定单元格的行为,例如空单元格,墙和目标单元格。可以使用其行和列索引来标识每个单元格。
通过此设置,可以方便地加载地图:
parser = MapParser()
gridMap = parser.parseMap("../data/map01.grid")载入
对于强化学习,我们需要能够处理一个策略π(s,a)π(s,a)。在gridworld中,每个状态ss代表代理的位置。这些动作将代理移动到四个地理方向之一。我们将使用以下符号将策略映射到地图上:
- N为动作
GO_NORTH - E为行动
GO_EAST - S为动作
GO_SOUTH - W为行动
GO_WEST
未知符号被映射到 NONE 操作 ,以获得完整的策略。
使用这些定义,我定义 了以下策略:
###################
#EESWWWWWWWWWWWWWX#
#EES###########SWN#
#EES#EEEEEEEES#SWN#
#EES#N#######S#SWN#
#EES#N#SSWWW#S#SWN#
#EEEEN#SS#NN#SWSWN#
#EENSSSSS#NNWWWWWN#
#EENWWWWEEEEEEEEEN#
###NNNNNNNNNNNNN###
#EENWWWWWWWWWWWWWW#
###################请注意,策略文件保留了围墙和目标单元,以提高可读性。该政策的制定有两个目标:
- 代理应该能够达到目标。 对于未实现此属性的策略,策略评估将不会给出合理的结果,因为永远不会获得目标回报。
- 该策略应该不是最理想的。这意味着在某些状态下,业务代表没有采取最短的路径达到目标。这样的策略使我们可以看到尝试改进初始策略的算法的效果。
为了加载该策略,我实现了一个 策略解析器,该解析器将策略存储为 策略对象。使用这些对象,我们可以像这样加载初始策略:
policyParser = PolicyParser()
policy = policyParser.parsePolicy("../data/map01.policy")策略对象具有用于建模π(s,a)π(s,a)的功能:
def pi(self, cell, action):
if len(self.policy) == 0:
# no policy: try all actions (for value iteration)
return 1
if self.policyActionForCell(cell) == action:
# policy allows this action
return 1
else:
# policy forbids this action
return 0强化学习的准备
为了准备实施强化学习算法,我们仍然需要提供过渡和奖励功能。
过渡函数
要定义转换函数Pass'Pss'a,我们首先需要区分非法行为和法律行为。在gridworld中,有两种方法可以使动作不合法:
- 如果该动作会使代理脱离网格
- 如果该动作会使代理人陷入困境
这为我们提供了转换函数的第一条规则:
1. When an action is illegal, the agent should remain in its previous state.此外,我们还必须要求:
2. When an action is illegal, transitions to states other than its previous state should be forbidden.当然,状态转换对于所选动作必须有效。由于每个动作仅将代理移动一个位置,因此建议状态s's'必须在与状态ss相邻的单元格中具有代理:
3. Only allow transitions through actions that would lead the agent to an adjacent cell.对于此规则,我们假设有一个谓词adj(s,s')adj(s,s')来指示主体从ss到s's'的过渡是否涉及相邻单元格。
最后,一旦达到目标状态s ∗ s ∗,我们就不希望代理再次离开。为了说明这一点,我们引入了最终规则:
4. Don't transition from the goal cell.基于这四个规则,我们可以定义转换函数如下:
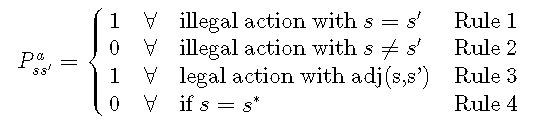
所提供的Python实现 getTransitionProbability 并不像数学公式那样明确 :
def getTransitionProbability(self, oldState, newState, action, gridWorld):
proposedCell = gridWorld.proposeMove(action)
if proposedCell is None:
# Rule 1 and 2: illegal move
return transitionProbabilityForIllegalMoves(oldState, newState)
if oldState.isGoal():
# Rule 4: stay at goal
return 0
if proposedCell != newState:
# Rule 3: move not possible
return 0
else:
# Rule 3: move possible
return 1
请注意,它 proposeMove 模拟了操作的成功执行,并返回了代理的新网格单元。
奖励函数
在gridworld中,我们想找到到达终端状态的最短路径。我们要最大化获得的奖励,因此目标状态s ∗ s ∗的奖励应高于其他状态的奖励。对于gridworld,我们将使用以下简单函数:
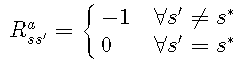
评估
策略评估算法的目标 是评估策略π(s,a)π(s,a),即根据V(s)∀sV(s)∀s确定所有状态的值。该算法基于Bellman方程:
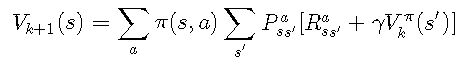
对于迭代k + 1k + 1,该方程式通过以下公式得出状态ss的值:
- π(s,a)π(s,a):在状态ss中选择动作aa的概率
- Pass'Pss'a:使用动作aa从状态ss过渡到状态s's'的概率
- Rass'Rss'a:使用动作aa从状态ss过渡到状态s's'时的预期奖励
- γγ:贴现率
- Vπk(s')Vkπ(s'):在给定策略ππ的情况下,步骤kk中状态s's'的值
为了更好地理解方程式,让我们在gridworld的上下文中逐一考虑:
- π(s,a)π(s,a):由于我们处于确定性环境中,因此策略仅指定一个动作aa,其中π(s,a)=1π(s,a)= 1,而所有其他动作a'a'具有π(s,a')=0π(s,a')= 0。因此,乘以π(s,a)π(s,a)只会选择策略指定的操作。
- ∑s′∑s′:该和是所有状态s′s′的总和,可以从当前状态ss得到。在gridworld中,我们只需要考虑相邻像元和当前像元本身,即s'∈{x | adj(x,s)∨x= s}s'∈{x | adj(x,s)∨x= s }。
- Pass'Pss'a:这是通过动作aa从状态ss过渡到s's'的概率。
- Rass'Rss'a:这是通过aa从ss过渡到s's'的奖励。请注意,在gridworld中,奖励仅由下一个状态s's'确定。
- γγ:折现因子调节预期奖励的影响。
- Vk(s')Vk(s'):在提议状态s's'的预期奖励。该术语的存在是政策评估是动态编程的原因:我们正在使用先前计算的值来更新当前值。
我们将使用γ=1γ= 1,因为我们处在一个情景 中,在达到目标状态时学习 停止。因此,值函数表示到达目标单元格的最短路径的长度。更准确地说,让d(s,s ∗)d(s,s ∗)表示从状态ss到目标的最短路径。然后,对于s≠s ∗ s≠s ∗,Vπ(s)=-d(s,s ∗)+1Vπ(s)=-d(s,s ∗)+ 1。
为了实施策略评估,我们通常将对状态空间进行多次扫描。每次扫描都需要前一次迭代中的值函数。新值和旧值函数之间的差异通常用作算法的终止条件:
def findConvergedCells(self, V_old, V_new, theta = 0.01):
diff = abs(V_old-V_new)
return np.where(diff < theta)[0]该函数确定值函数差异小于θθ的网格单元的索引。当所有状态的值都收敛到稳定值时,我们可以停止。由于情况并非总是如此(例如,如果策略指定状态的动作不会导致目标,或者过渡概率/奖励配置不当),我们还要指定最大迭代次数。
达到停止条件后, evaluatePolicy 返回最新的状态值函数:
def evaluatePolicy(self, gridWorld, gamma = 1):
if len(self.policy) != len(gridWorld.getCells()):
# sanity check whether policy matches dimension of gridWorld
raise Exception("Policy dimension doesn't fit gridworld dimension.")
maxIterations = 500
V_old = None
V_new = initValues(gridWorld) # sets value of 0 for viable cells
iter = 0
convergedCellIndices = np.zeros(0)
while len(ConvergedCellIndices) != len(V_new):
V_old = V_new
iter += 1
V_new = self.evaluatePolicySweep(gridWorld, V_old, gamma, convergedCellIndices)
convergedCellIndices = self.findConvergedCells(V_old, V_new)
if iter > maxIterations:
break
print("Policy evaluation converged after iteration: " + str(iter))
return V_new该evaluatePolicySweep 功能执行一次策略评估扫描 。该函数遍历网格中的所有单元并确定状态的新值.
请注意,该 ignoreCellIndices 参数表示后续扫描未更改值函数的像元索引。这些单元在进一步的迭代中将被忽略以提高性能。这对于我们的gridworld示例来说很好,因为我们只是想找到最短的路径。因此,状态值函数第一次不变时,这是其最佳值。
使用该evaluatePolicyForState 函数计算状态值 。该函数的核心实现了我们先前讨论的Bellman方程。此函数的重要思想是,在计算状态ss的值函数时,我们不想扫描所有状态s's'。这就是为什么 状态生成器 仅生成可能实际发生的状态(即,转换概率大于零)的原因。
评估结果
有了适当的实现后,我们可以通过执行以下命令找到策略的状态值函数.
为了将值函数与策略一起绘制,我们可以在将用于表示地图的一维数组转换为二维数组后,使用matplotlib中的pyplot:
def drawValueFunction(V, gridWorld, policy):
fig, ax = plt.subplots()
im = ax.imshow(np.reshape(V, (-1, gridWorld.getWidth())))
for cell in gridWorld.getCells():
p = cell.getCoords()
i = cell.getIndex()
if not cell.isGoal():
text = ax.text(p[1], p[0], str(policy[i]),
ha="center", va="center", color="w")
if cell.isGoal():
text = ax.text(p[1], p[0], "X",
ha="center", va="center", color="w")
plt.show()使用该函数,我们可以可视化策略的状态值函数:
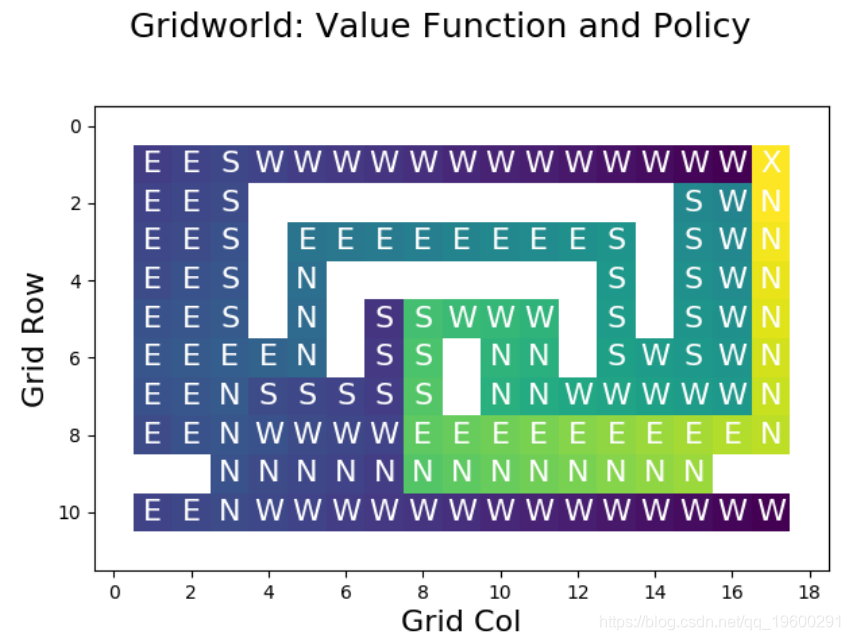
对于非目标单元,将使用策略指定的操作对图进行注释。X 标签上方表示右上方单元格中的目标 。
其他单元格的值由颜色指示。最差的状态(具有最低的奖励)以紫色显示,坏的状态以蓝色显示,蓝绿色的中间状态以绿色显示,良好的状态以绿色显示,非常好的状态(具有最高的奖励)显示为黄色。
查看这些值,我们可以看到结果与策略规定的操作相匹配。例如,直接位于目标西侧的状态的值非常低,因为该状态的动作(GO_WEST)会导致较长的弯路。位于目标正南方的单元格具有很高的价值,因为其作用(GO_NORTH)直接导致目标。
请注意,在以后的工作中,的性能 evaluatePolicy 至关重要,因为我们会多次调用它。对于计算的示例,该函数需要进行61次迭代,这在我的笔记本电脑上大约转换了半秒钟。请注意,对于更接近最佳策略的策略,策略评估将需要较少的迭代,因为值将更快地传播。
能够确定状态值函数非常好-现在我们可以量化所提议策略的优点了。但是,我们尚未解决寻找最佳政策的问题。这就是策略迭代起作用的地方。
策略迭代
现在我们已经能够计算状态值函数,我们应该能够 改进现有的策略。一种简单的策略是贪婪算法,该算法遍历网格中的所有单元格,然后根据值函数选择使预期奖励最大化的操作。
其定义为
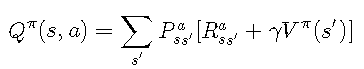
improvePolicy 函数确定策略的值函数 ,然后调用 findGreedyPolicy 以标识每种状态的最佳操作.
要做的 findGreedyPolicy 是考虑每个单元并选择使预期奖励最大化的动作,从而构造输入策略的改进版本。例如,执行 improvePolicy 一次并重新评估策略后,我们得到以下结果:
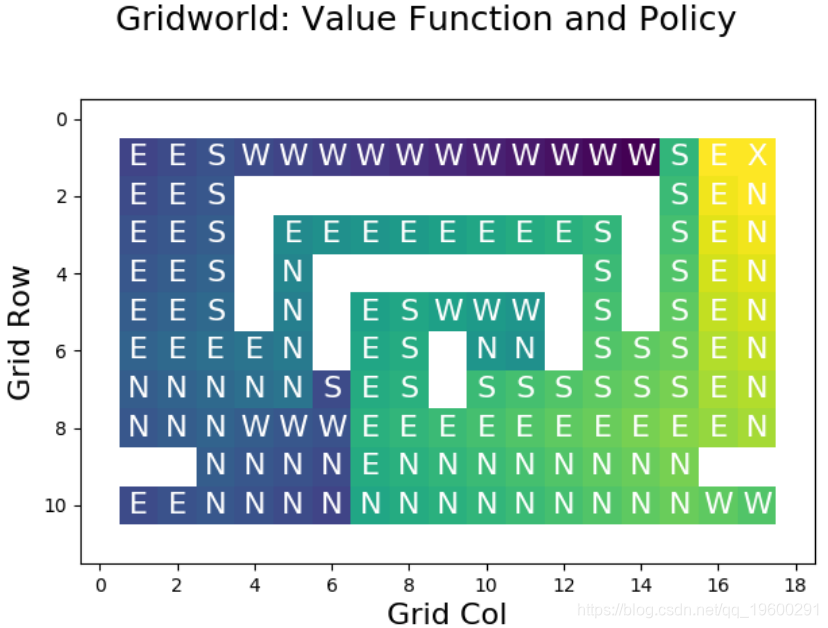
与原始值函数相比,目标旁边的所有单元格现在都给了我们很高的回报,因为操作已得到优化。但是,我们可以看到这些改进仅仅是局部的。那么,我们如何获得最优政策呢?
策略迭代算法的思想 是,我们可以通过 迭代评估新策略的状态值函数来找到最优策略,并使用贪心算法对该策略进行改进,直到达到最优:
def policyIteration(policy, gridWorld):
lastPolicy = copy.deepcopy(policy)
lastPolicy.resetValues() # reset values to force re-evaluation of policy
improvedPolicy = None
while True:
improvedPolicy = improvePolicy(lastPolicy, gridWorld)
if improvedPolicy == lastPolicy:
break
improvedPolicy.resetValues() # to force re-evaluation of values on next run
lastPolicy = improvedPolicy
return(improvedPolicy)策略迭代的结果
在gridworld上运行该算法可以在20次迭代中找到最佳解决方案-在我的笔记本上大约需要4.5秒。20次迭代后的终止并不令人惊讶:gridworld贴图的宽度为19。因此,我们需要进行19次迭代才能优化水平走廊的值。然后,我们需要进行一次额外的迭代来确定该算法可以终止,因为该策略未更改。
理解策略迭代的一个很好的工具是可视化每个迭代:
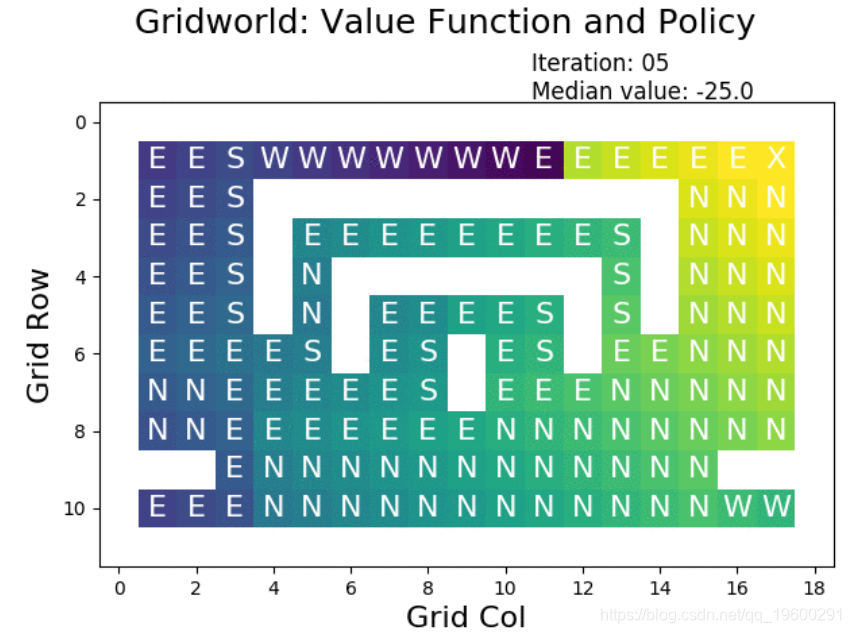
下图显示了使用策略迭代构造的最优值函数:
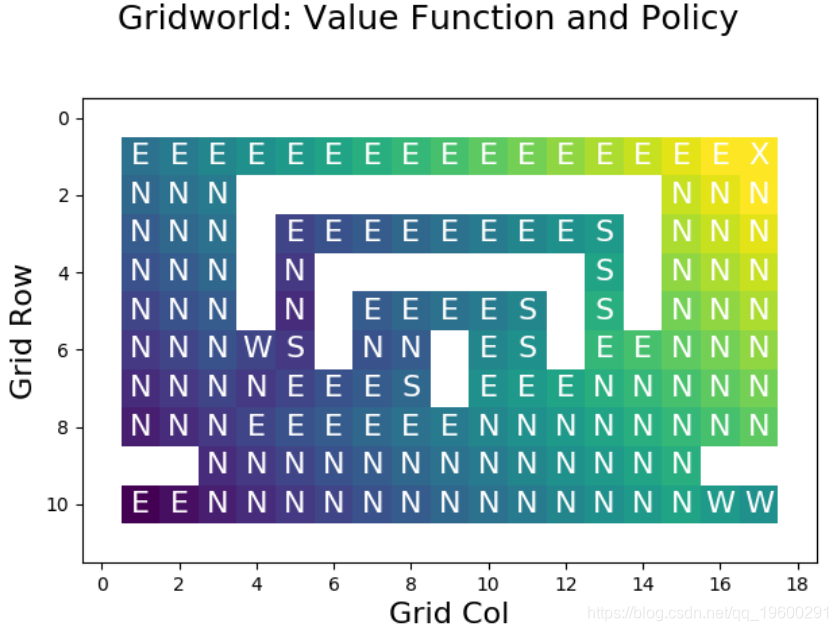
目视检查表明值函数正确,因为它为网格中的每个单元格选择了最短路径。
价值迭代
借助我们迄今为止探索的工具,出现了一个新问题:为什么我们根本需要考虑初始策略?价值迭代算法的思想 是我们可以在没有策略的情况下计算价值函数。与其让政策ππ指示选择了哪些操作,我们不选择那些使预期奖励最大化的操作:
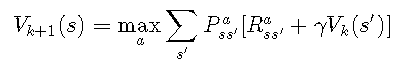
因为价值迭代的计算与策略评估非常相似,所以我已经实现了将价值迭代evaluatePolicyForState 用于我先前定义的方法中的功能 。
只要没有可用的策略,此函数就会执行值迭代算法。在这种情况下, len(self.policy) 将为零,从而 pi 始终返回一个值,并且 V 被确定为所有动作的预期奖励的最大值。
因此,要实现值迭代,我们不必做很多编码。我们只需要evaluatePolicySweep 在Policy 对象的值函数未知的情况下迭代调用该 函数, 直到该过程为我们提供最佳结果为止。然后,要确定相应的策略,我们只需调用findGreedyPolicy 我们先前定义的 函数.
价值迭代的结果
当执行值迭代时,奖励(高:黄色,低:黑暗)从目标的最终状态(右上方 X)扩展到其他状态:
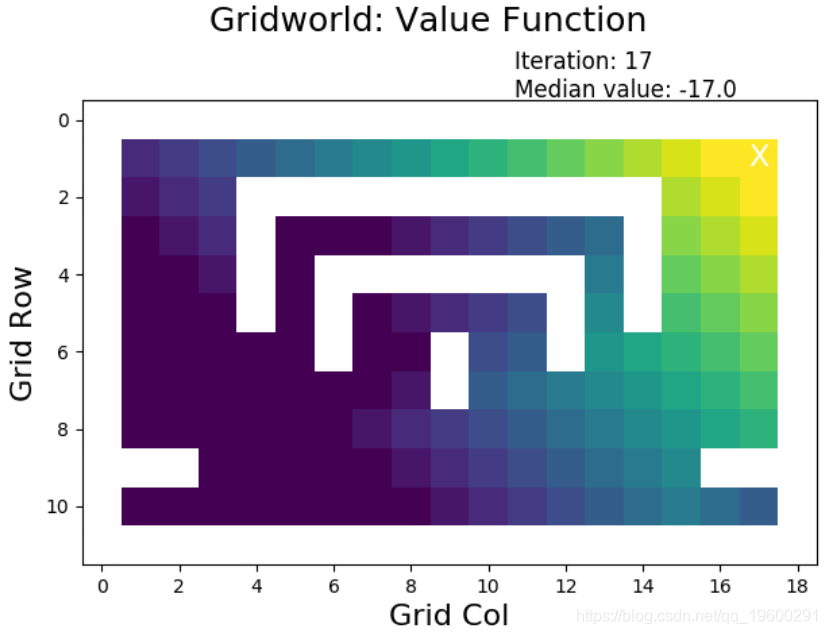
摘要
我们已经看到了如何在MDP中应用强化学习。我们的工作假设是我们对环境有全面的了解,并且代理完全了解环境。基于此,我们能够促进动态编程来解决三个问题。首先,我们使用策略评估来确定给定策略的状态值函数。接下来,我们应用策略迭代算法来优化现有策略。第三,我们应用价值迭代从头开始寻找最佳策略。