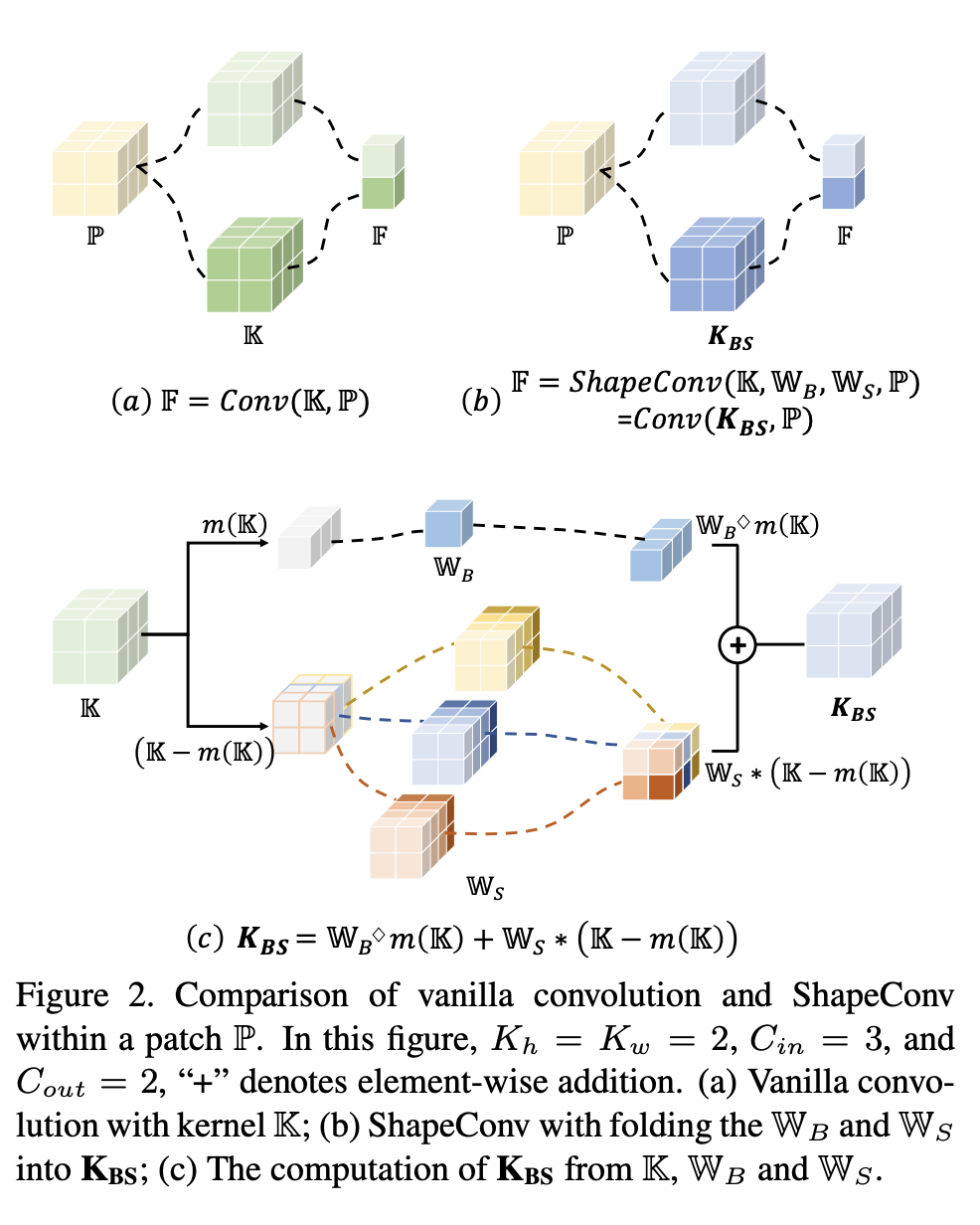
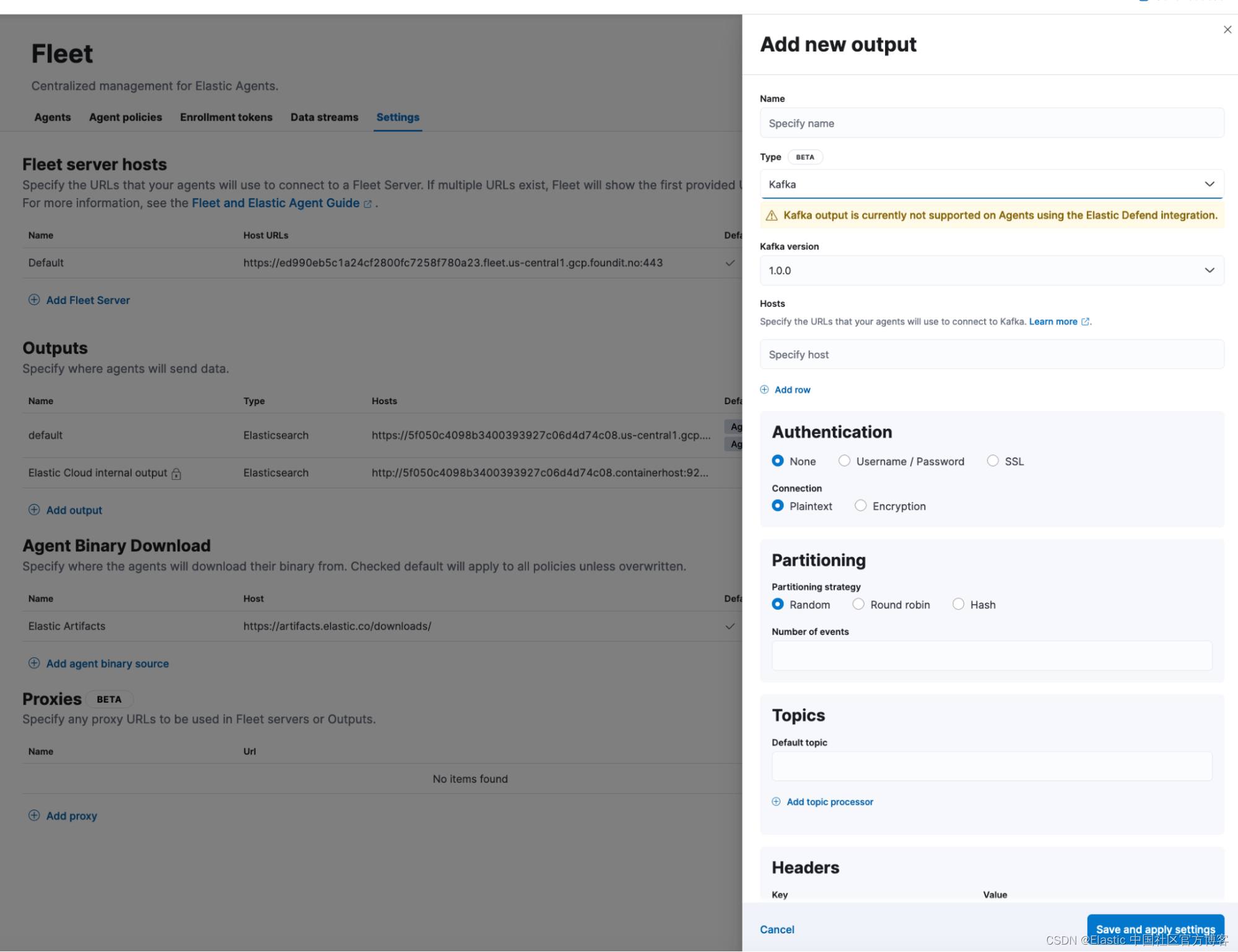
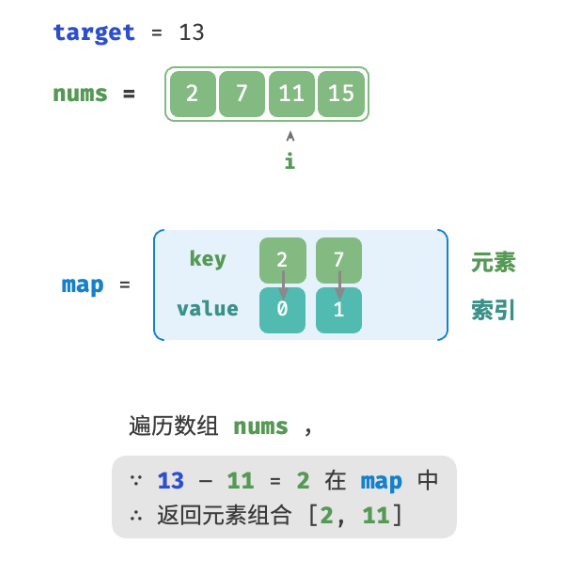
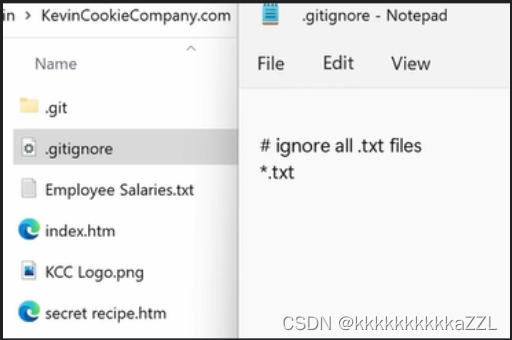
分治（例题1）九键电话号码的字母组合

电话号码的字⺟组合给定⼀个仅包含数字 2-9 的字符串，返回所有它能表示的字⺟组合。答案可以按任意顺序返回。给出数字到字⺟的映射如下（与电话按键相同）。注意 1 不对应任何字⺟

•

• 示例 1：输⼊：digits = "23" 输出：[“ad","ae","af","bd","be","bf","cd","ce","cf"]

• 示例 2：输⼊：digits = "" 输出：[]

• 示例 3：输⼊：digits = "2" 输出：[“a","b","c"]

leetcode17

d={2:'abc',3:'def',4:'ghi',
   5:'jkl',6:'mno',7:'pqrs',
   8:'tuv',9:'wxyz'
   }

res=[]
def gene(digits,i,s):
    if len(digits)==len(s):  #
        res.append(s)
        return

    m=d[int(digits[i])]   # 获得对应字母 digits[i]为str类型

    for a in m:
        gene(digits,i+1,s+a)  # 进入下一层  i加1 递归下一个位置 s+a保存当前字母


digits='29'   # str类型
gene(digits,0,'')
print(res)

没太懂

分治（例题2）实现 pow(x, n) ，即计算 x 的 n 次幂函数

• 示例 1:

• 输⼊: 2.00000, 10

• 输出: 1024.00000

• 示例 2:

• 输⼊: 2.10000, 3

• 输出: 9.26100

• 示例 3:

• 输⼊: 2.00000, -2

• 输出: 0.25000

• 解释: 2-2 = 1/22 = 1/4 = 0.25

def pow(x,n):
    if n==1:
        return x

    y=pow(x,n//2)
    if n%2==0:
        return y*y
    else:
        return y*y*x

没太懂

回溯（例题3）八皇后问题

在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同⼀⾏、同⼀列或同⼀斜线上，问有多少种摆法。

回溯法：有冲突解决冲突，没有冲突往前⾛，⽆路可⾛往回退，⾛到最后是答案。

'''


递归参数:
     n: n皇后
     i: 递归到第几行 0
     l: 记录路径结果 [-1]*n


标记list：  lie=[]
           zXie=[]
           fXie=[]
'''

lie=[]
zXie=[]
fXie=[]
res=[]
def que(n,i,l):
    if n==i:
        res.append(l[:])
        return

    for j in range(n):  # 查找i行存放的位置
        if (j not in lie) and (i+j not in zXie) and (i-j not in fXie):  # j为可以放
            lie.append(j)
            zXie.append(i+j)
            fXie.append(i-j)
            l[i]=j
            que(n,i+1,l)
            lie.remove(j)
            zXie.remove(i+j)
            fXie.remove(i-j)
            l[i]=-1

l=[-1]*4
que(4,0,l)
print(res)

回溯（例题4）求⼦集

给你⼀个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的⼦集。

解集不能包含重复的⼦集。你可以按任意顺序返回解集。

示例 1：

输⼊：nums = [1,2,3]

输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输⼊：nums = [0]

输出：[[],[0]]

'''

i: 下一次开始的位置
n: nums的长度
l:记录结果  []

'''

res=[]  # 最终结果
def gene(nums,i,n,l):
    res.append(l)
    for j in range(i,n):
        gene(nums,j+1,n,l+[nums[j]])

nums=[1,2,3]
n=len(nums)
gene(nums,0,n,[])
print(res)