核心思想：把 $a,b$ 化成 $fwt(a),fwt(b)$，相乘后再化为 $a$

化的过程用的是分治

所以和FFT其实一模一样

OR / AND 卷积

不需要什么技巧，暴力分治转移即可

每次分治下去，相当于位数减一

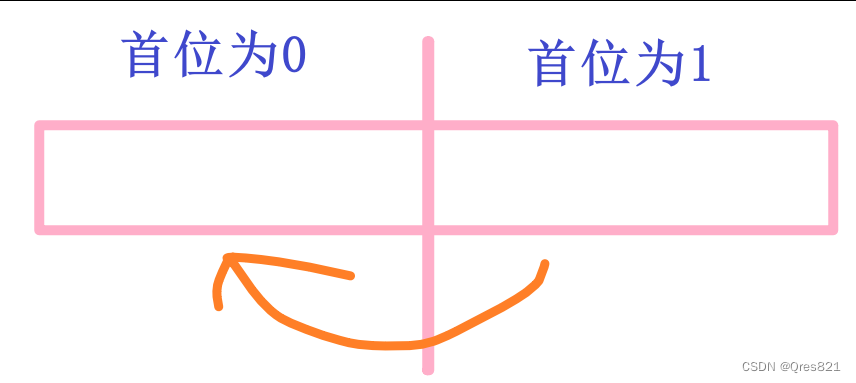
注意合并过程中我们是计算对应位的贡献

因为其它位的贡献我们在分治下去时已经计算了

后面区间其他数贡献到前面某个位置已经统计到后面的那个位置了

OR

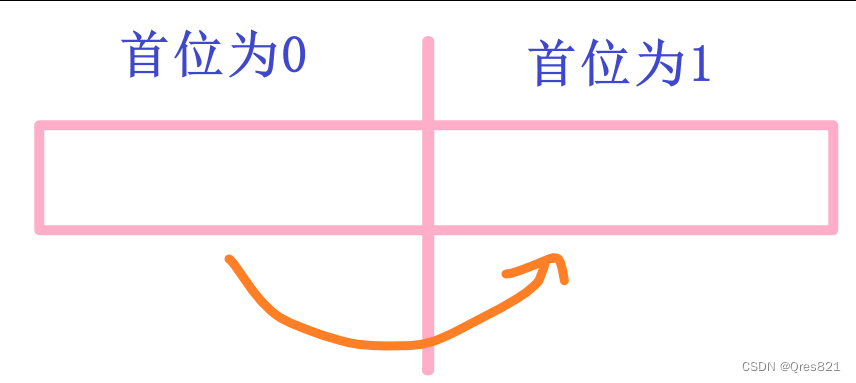
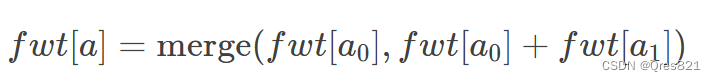
考虑如何还原

对上面式子进行换元即可

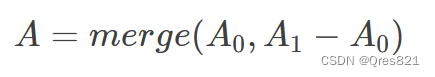
void OR(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1)
		for(i=0; i<n; i+=o)
			for(j=0; j<k; ++j) 
				f[i+j+k]=(f[i+j+k]+f[i+j]*x)%mo; 
}

AND

反过来好像就行了

void AND(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1)
		for(i=0; i<n; i+=o)
			for(j=0; j<k; ++j) 
				f[i+j]=(f[i+j]+f[i+j+k]*x)%mo; 
}

XOR卷积

这个需要点技巧

首先考虑若有转移系数，必须满足以下条件：

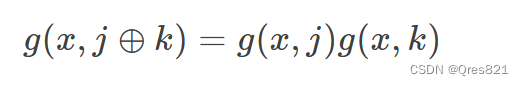
我们可以用以下方法构造：

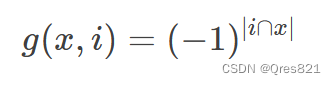
构造的原理：

异或前后 1 的个数的奇偶性不变

因此得证：

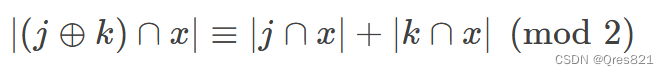
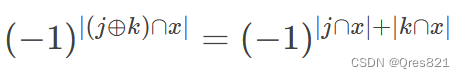
所以有：

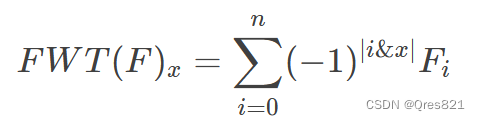
我们把它写成这个形式：

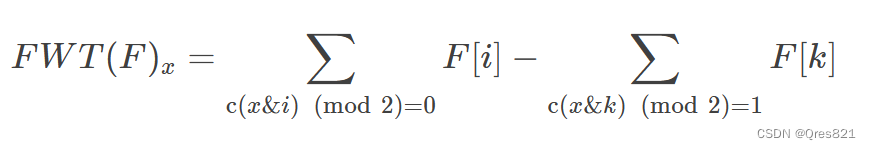
然后考虑如何FWT和IFWT

思考分治过程中popcount的变化

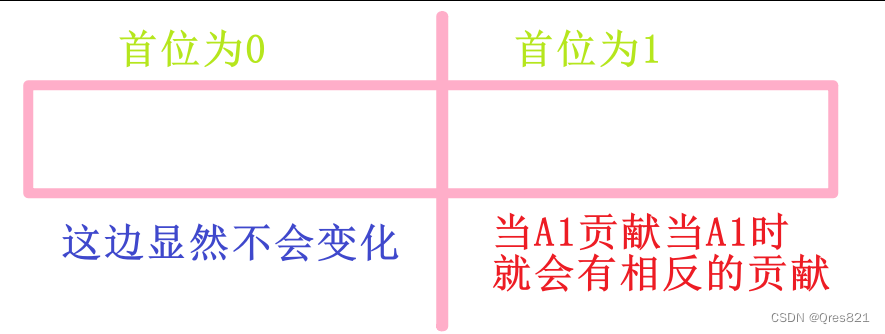
因此合并的过程可以表示为：

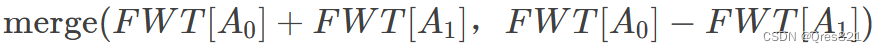
换元一下可以得到其逆变换：

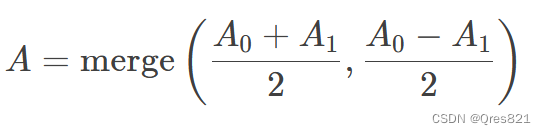
void XOR(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1) 
		for(i=0; i<n; i+=o) 
			for(j=0; j<k; ++j) {
				f[i+j]+=f[i+j+k]; 
				f[i+j+k]=f[i+j]-2*f[i+j+k]; 
				f[i+j]=f[i+j]*x%mo; f[i+j+k]=f[i+j+k]*x%mo; 
			}
}

板子

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
#define mo 998244353
#define N 200010
int pw(int a, int b) {
	int ans=1; 
	while(b) {
		if(b&1) ans*=a; 
		a*=a; b>>=1; 
		ans%=mo; a%=mo; 
	}
	return ans; 
}
const int inv2=pw(2, mo-2); 
int n, m, i, j, k, T;
int a[N], b[N], A[N], B[N], o; 

void cp() {
	for(i=0; i<n; ++i) a[i]=A[i], b[i]=B[i]; 
}

void pr() {
	for(i=0; i<n; ++i) printf("%lld ", (a[i]%mo+mo)%mo); 
	printf("\n"); 
}

void mul() {
	for(i=0; i<n; ++i) a[i]=a[i]*b[i]%mo; 
}

void OR(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1)
		for(i=0; i<n; i+=o)
			for(j=0; j<k; ++j) 
				f[i+j+k]=(f[i+j+k]+f[i+j]*x)%mo; 
}

void AND(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1)
		for(i=0; i<n; i+=o)
			for(j=0; j<k; ++j) 
				f[i+j]=(f[i+j]+f[i+j+k]*x)%mo; 
}

void XOR(int *f, int x) {
	for(k=1, o=2; o<=n; o<<=1, k<<=1) 
		for(i=0; i<n; i+=o) 
			for(j=0; j<k; ++j) {
				f[i+j]+=f[i+j+k]; 
				f[i+j+k]=f[i+j]-2*f[i+j+k]; 
				f[i+j]=f[i+j]*x%mo; f[i+j+k]=f[i+j+k]*x%mo; 
			}
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
//	srand(time(NULL));
//	T=read();
//	while(T--) {
//
//	}
	n=read(); n=(1<<n); 
	for(i=0; i<n; ++i) A[i]=read(); 
	for(i=0; i<n; ++i) B[i]=read(); 
	cp(); OR(a, 1); OR(b, 1); mul(); OR(a, -1); pr(); 
	cp(); AND(a, 1); AND(b, 1); mul(); AND(a, -1); pr(); 
	cp(); XOR(a, 1); XOR(b, 1); mul(); XOR(a, inv2); pr(); 
	return 0;
}