怒刷LeetCode的第2天（Java版）

news2024/11/26 1:32:09

目录

第一题

题目来源

题目内容

解决方法

方法一：滑动窗口

方法二：双指针加哈希表

第二题

题目来源

题目内容

解决方法

方法一：二分查找

方法二：归并排序

方法三：分治法

第三题

题目来源

题目内容

解决方法

方法一：动态规划

方法二：中心扩展法

方法三：Manacher 算法

第一题

题目来源

3. 无重复字符的最长子串 - 力扣（LeetCode）

题目内容

解决方法

方法一：滑动窗口

该问题可以使用滑动窗口算法来解决。滑动窗口是一种通过移动窗口的起始和结束位置来解决字符串/数组子串问题的常用技巧。

具体算法步骤如下：

  1. 定义一个哈希集合，用于存储当前窗口中的字符。
  2. 使用两个指针left和right分别表示窗口的起始和结束位置，初始化为0。
  3. 使用一个循环遍历字符串s，不断移动右指针来扩展窗口。当右指针指向的字符在哈希集合中存在时，说明窗口中出现了重复字符。
  4. 在每一次循环中，首先判断右指针指向的字符是否在哈希集合中存在，如果不存在，则将该字符加入集合，并更新最长无重复子串的长度为maxLen（即maxLen = max(maxLen, right - left + 1)）。
  5. 如果右指针指向的字符在哈希集合中存在，则从窗口的左侧开始移动左指针，直到窗口中不再有重复字符。
  6. 重复步骤3-5，直到右指针到达字符串s的末尾。
  7. 返回最长无重复子串的长度maxLen。
class Solution {
   public int lengthOfLongestSubstring(String s) {
    int n = s.length();
    Set<Character> set = new HashSet<>();
    int maxLen = 0, left = 0, right = 0;
    
    while (right < n) {
        if (!set.contains(s.charAt(right))) {
            set.add(s.charAt(right));
            maxLen = Math.max(maxLen, right - left + 1);
            right++;
        } else {
            set.remove(s.charAt(left));
            left++;
        }
    }
    
    return maxLen;
}
}

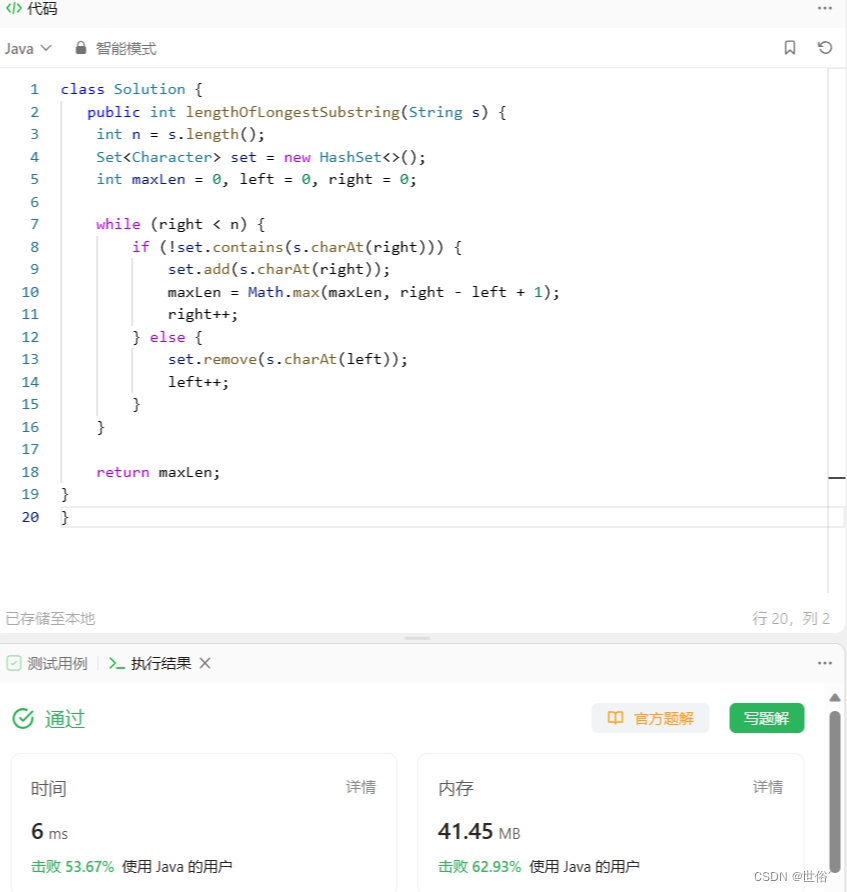
该算法的时间复杂度为O(n)，其中n是字符串s的长度。在最坏情况下，每个字符都需要遍历一次。空间复杂度为O(min(n, m))，其中m是字符集的大小。在最坏情况下，窗口中可能包含所有的字符。 

LeetCode运行结果：

方法二：双指针加哈希表

除了滑动窗口算法之外，还可以使用双指针加哈希表来解决该问题。

具体算法步骤如下：

  1. 定义一个哈希表map，用于存储字符和它在字符串中出现的位置。
  2. 使用两个指针left和right分别表示当前无重复子串的起始和结束位置，初始化为0。
  3. 使用一个循环遍历字符串s，不断移动右指针来扩展窗口。当右指针指向的字符在哈希表中存在时，说明窗口中出现了重复字符。
  4. 在每一次循环中，首先判断右指针指向的字符是否在哈希表中存在，如果不存在，则将该字符加入哈希表，并更新最长无重复子串的长度为maxLen（即maxLen = max(maxLen, right - left + 1)）。
  5. 如果右指针指向的字符在哈希表中存在，则从哈希表中获取该字符最新的出现位置pos，并将左指针移动到pos+1的位置。
  6. 更新哈希表中该字符的最新出现位置为右指针指向的位置right+1（注意要加1，因为要排除当前字符的影响），然后将右指针继续右移一位。
  7. 重复步骤3-6，直到右指针到达字符串s的末尾。
  8. 返回最长无重复子串的长度maxLen。
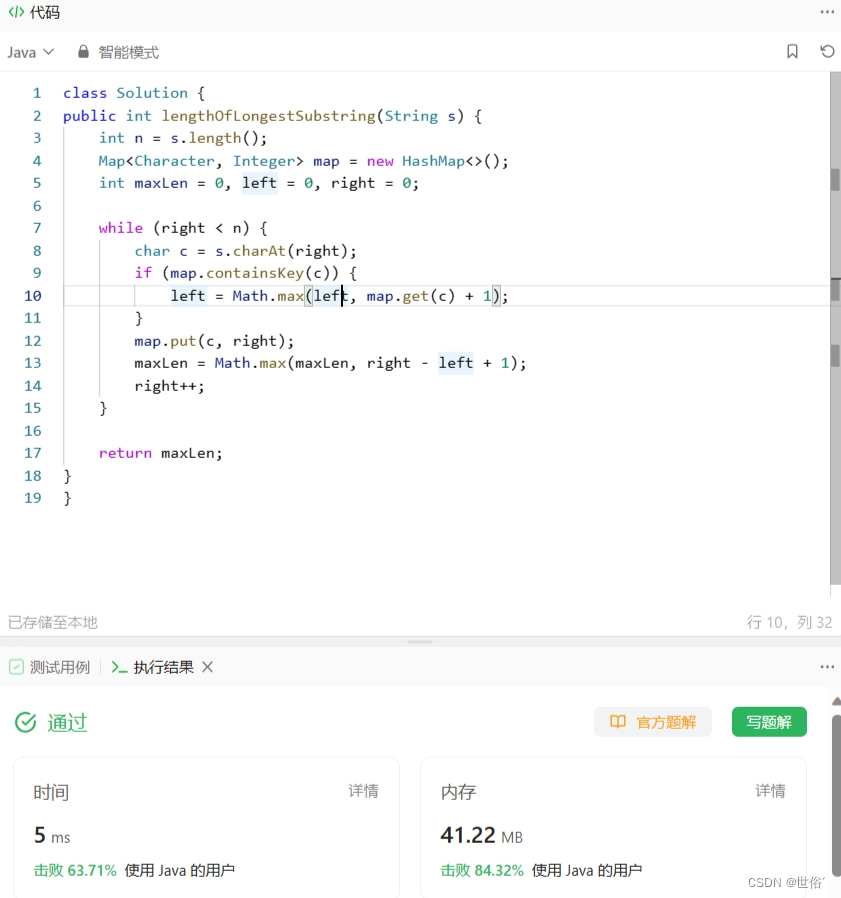
class Solution {
public int lengthOfLongestSubstring(String s) {
    int n = s.length();
    Map<Character, Integer> map = new HashMap<>();
    int maxLen = 0, left = 0, right = 0;
    
    while (right < n) {
        char c = s.charAt(right);
        if (map.containsKey(c)) {
            left = Math.max(left, map.get(c) + 1);
        }
        map.put(c, right);
        maxLen = Math.max(maxLen, right - left + 1);
        right++;
    }
    
    return maxLen;
}
}

该算法的时间复杂度为O(n)，其中n是字符串s的长度。在最坏情况下，每个字符都需要遍历一次。空间复杂度为O(min(n, m))，其中m是字符集的大小。在最坏情况下，哈希表中可能包含所有的字符。

LeetCode运行结果：

第二题

题目来源

4. 寻找两个正序数组的中位数 - 力扣（LeetCode）

题目内容

解决方法

方法一：二分查找

本题可以使用二分查找求解，时间复杂度为O(log(min(m, n)))。

由于两个数组都是有序的，所以可以先将问题转化为寻找第k小的数，其中k等于两个数组的长度之和除以2。如果两个数组长度之和是奇数，则中位数就是第k小的数；如果长度之和是偶数，则中位数是第k小和第k+1小数的平均值。

具体算法如下：

  1. 设两个有序数组为nums1和nums2，分别对它们进行二分查找。
  2. 假设nums1的长度为m，nums2的长度为n，则第k小的数就是最小的第k/2个数。
  3. 比较nums1[k/2-1]和nums2[k/2-1]。如果nums1[k/2-1] < nums2[k/2-1]，说明nums1中的前k/2个数一定包含在中位数的前k个数中。反之，如果nums1[k/2-1] > nums2[k/2-1]，说明nums2中的前k/2个数一定包含在中位数的前k个数中。
  4. 根据步骤3中的比较结果，确定接下来需要在哪个子数组中查找，然后递归调用本函数，更新k和目标数组。特别注意，每次递归调用时，都需要更新数组的起始下标，使得两个子数组的长度之和为k。
  5. 重复步骤3-4，直到k为1或者有一个数组为空，则中位数即为两个数组中剩余元素的第一个。
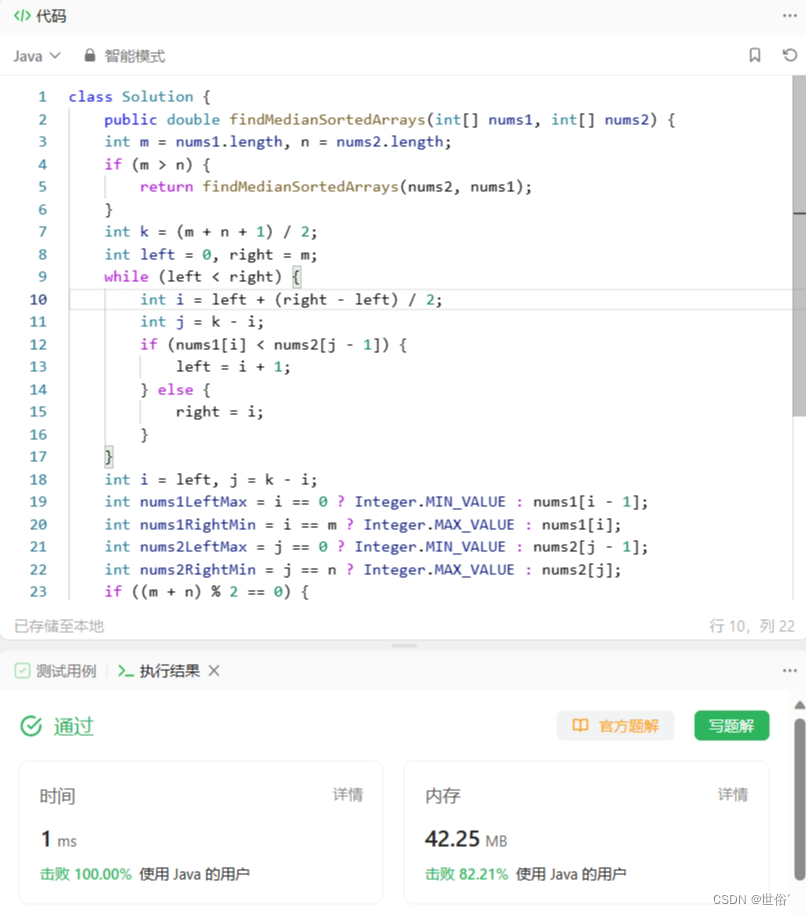
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int m = nums1.length, n = nums2.length;
    if (m > n) {
        return findMedianSortedArrays(nums2, nums1);
    }
    int k = (m + n + 1) / 2;
    int left = 0, right = m;
    while (left < right) {
        int i = left + (right - left) / 2;
        int j = k - i;
        if (nums1[i] < nums2[j - 1]) {
            left = i + 1;
        } else {
            right = i;
        }
    }
    int i = left, j = k - i;
    int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];
    int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];
    int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];
    int nums2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];
    if ((m + n) % 2 == 0) {
        return (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin)) / 2.0;
    } else {
        return Math.max(nums1LeftMax, nums2LeftMax);
    }
}

}

该算法的时间复杂度为O(log(min(m, n)))，空间复杂度为O(1)。 

LeetCode运行结果：

方法二：归并排序

还有另一种方法可以解决这个问题，即使用归并排序的思想。具体步骤如下：

  1. 创建一个新的数组，用于存储合并后的两个有序数组。
  2. 使用两个指针分别指向nums1和nums2的起始位置。
  3. 每次比较两个数组当前指针所指的元素，将较小的元素添加到新数组中，并将对应的指针向后移动一位。
  4. 重复步骤3，直到其中一个数组的指针到达末尾。
  5. 将另一个数组剩余的元素依次添加到新数组的末尾。
  6. 如果新数组的长度是奇数，则中位数就是新数组的中间元素；如果新数组的长度是偶数，则中位数是中间两个元素的平均值。

该方法的时间复杂度为O(m + n)，其中m和n分别是两个数组的长度。空间复杂度为O(m + n)，主要用于存储合并后的数组。 

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int m = nums1.length, n = nums2.length;
    int[] merged = new int[m + n];
    int i = 0, j = 0, k = 0;
    while (i < m && j < n) {
        if (nums1[i] <= nums2[j]) {
            merged[k++] = nums1[i++];
        } else {
            merged[k++] = nums2[j++];
        }
    }
    while (i < m) {
        merged[k++] = nums1[i++];
    }
    while (j < n) {
        merged[k++] = nums2[j++];
    }
    if ((m + n) % 2 == 0) {
        int mid = (m + n) / 2;
        return (merged[mid - 1] + merged[mid]) / 2.0;
    } else {
        int mid = (m + n) / 2;
        return merged[mid];
    }
}

}

LeetCode运行结果：

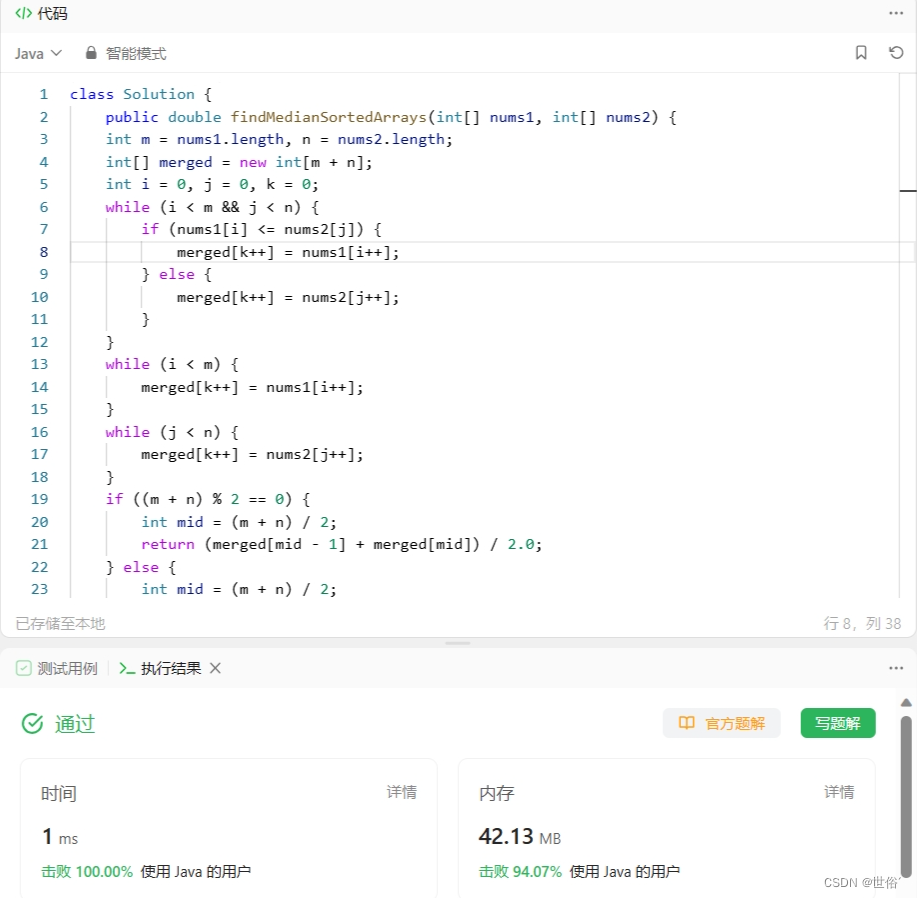
方法三：分治法

除了上述两种方法，还可以使用分治法来解决这个问题。该方法的思路是将问题分解为两个子问题，然后对子问题进行递归求解。

具体步骤如下：

  1. 分别找到两个数组的中位数，假设分别为nums1[mid1]和nums2[mid2]，其中mid1和mid2分别表示两个数组的中间位置。
  2. 如果nums1[mid1]等于nums2[mid2]，则说明中位数已经找到，直接返回nums1[mid1]或nums2[mid2]。
  3. 如果nums1[mid1]小于nums2[mid2]，则说明中位数应该在nums1[mid1]的右侧和nums2[mid2]的左侧。
    • 在nums1[mid1]的右侧舍弃掉前mid1+1个元素，并且将k减去mid1+1。
    • 在nums2[mid2]的左侧舍弃掉后mid2个元素。
  4. 如果nums1[mid1]大于nums2[mid2]，则说明中位数应该在nums1[mid1]的左侧和nums2[mid2]的右侧。
    1. 在nums1[mid1]的左侧舍弃掉后mid1个元素。
    2. 在nums2[mid2]的右侧舍弃掉前mid2+1个元素，并且将k减去mid2+1。
  5. 重复上述步骤3和步骤4，直到找到中位数为止。

这种方法的时间复杂度也为O(log(min(m, n)))，空间复杂度为O(1)。与二分查找类似，它通过逐渐缩小问题规模来快速找到中位数。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int m = nums1.length, n = nums2.length;
    int total = m + n;
    if (total % 2 == 1) { // 奇数长度，中位数是第 total/2 + 1 个元素
        return getKthElement(nums1, nums2, total / 2 + 1);
    } else { // 偶数长度，中位数是第 total/2 个元素和第 total/2 + 1 个元素的平均值
        double left = getKthElement(nums1, nums2, total / 2);
        double right = getKthElement(nums1, nums2, total / 2 + 1);
        return (left + right) / 2.0;
    }
}

private int getKthElement(int[] nums1, int[] nums2, int k) {
    int m = nums1.length, n = nums2.length;
    int index1 = 0, index2 = 0;
    while (true) {
        // 边界情况：一个数组的所有元素都被剔除
        if (index1 == m) {
            return nums2[index2 + k - 1];
        }
        if (index2 == n) {
            return nums1[index1 + k - 1];
        }
        // 边界情况：k=1，即找到了最小的一个数
        if (k == 1) {
            return Math.min(nums1[index1], nums2[index2]);
        }
        // 正常情况
        int newIndex1 = Math.min(index1 + k / 2, m) - 1;
        int newIndex2 = Math.min(index2 + k / 2, n) - 1;
        int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
        if (pivot1 <= pivot2) {
            k -= newIndex1 - index1 + 1;
            index1 = newIndex1 + 1;
        } else {
            k -= newIndex2 - index2 + 1;
            index2 = newIndex2 + 1;
        }
    }
}

}

LeetCode运行结果：

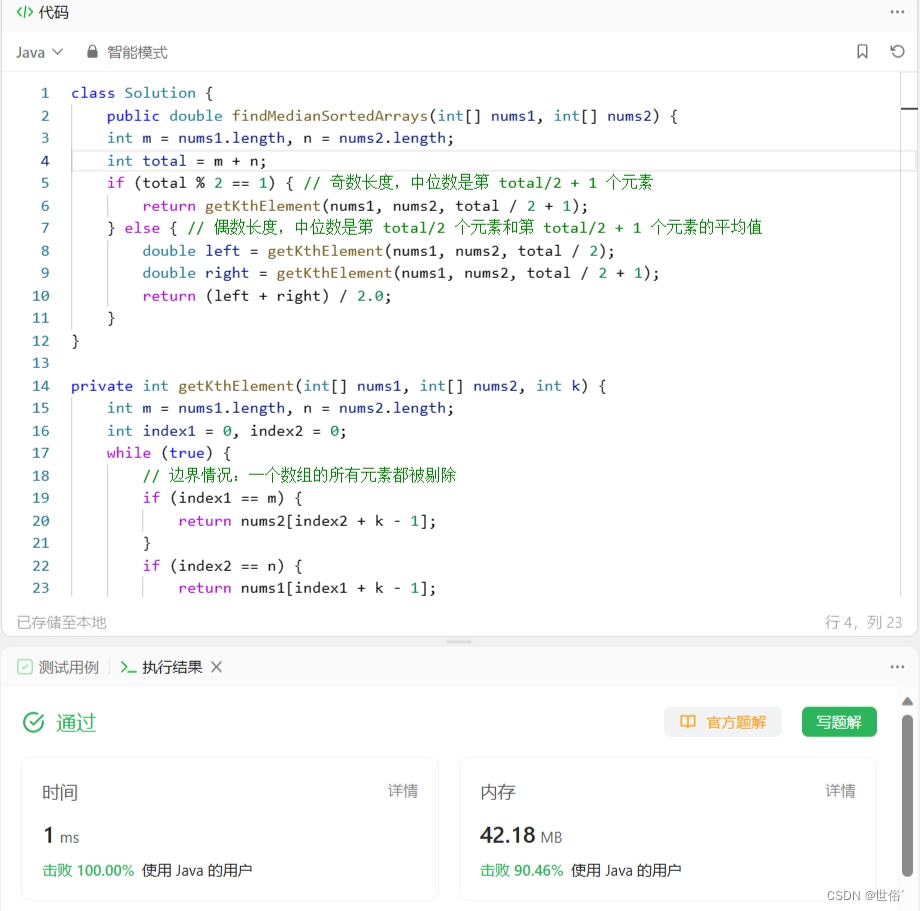
第三题

题目来源

5. 最长回文子串 - 力扣（LeetCode）

题目内容

​

解决方法

方法一：动态规划

这道题可以使用动态规划来解决，具体步骤如下：

  1. 定义一个二维布尔数组dp，其中dp[i][j]表示字符串s中从索引i到索引j的子串是否是回文子串。初始化时，将所有的dp[i][i]设为true，表示单个字符都是回文串。
  2. 从右下角开始，按列从下往上逐列填表。先计算长度为2的子串是否是回文子串，再计算长度为3的子串，依次类推，直到计算出整个字符串的最长回文子串长度为止。
    如果dp[i+1][j-1]为true（即子串s[i+1:j-1]也是回文子串）且s[i]等于s[j]，则dp[i][j]为true，否则为false。 
  3. 在计算的过程中，记录并更新最长回文子串的起始索引和长度。
  4. 最后，根据最长回文子串的起始索引和长度，提取出最长回文子串。
class Solution {
    public String longestPalindrome(String s) {
    int n = s.length();
    boolean[][] dp = new boolean[n][n];
    int maxLen = 0;
    int start = 0;

    for (int j = 0; j < n; j++) {
        for (int i = j; i >= 0; i--) {
            if (s.charAt(i) == s.charAt(j) && (j - i <= 2 || dp[i + 1][j - 1])) {
                dp[i][j] = true;
                if (j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    start = i;
                }
            }
        }
    }

    return s.substring(start, start + maxLen);
}

}

该算法的时间复杂度为O(n^2)，空间复杂度为O(n^2)，其中n为字符串的长度。通过动态规划，我们可以高效地找到最长回文子串。 

LeetCode运行结果：

  

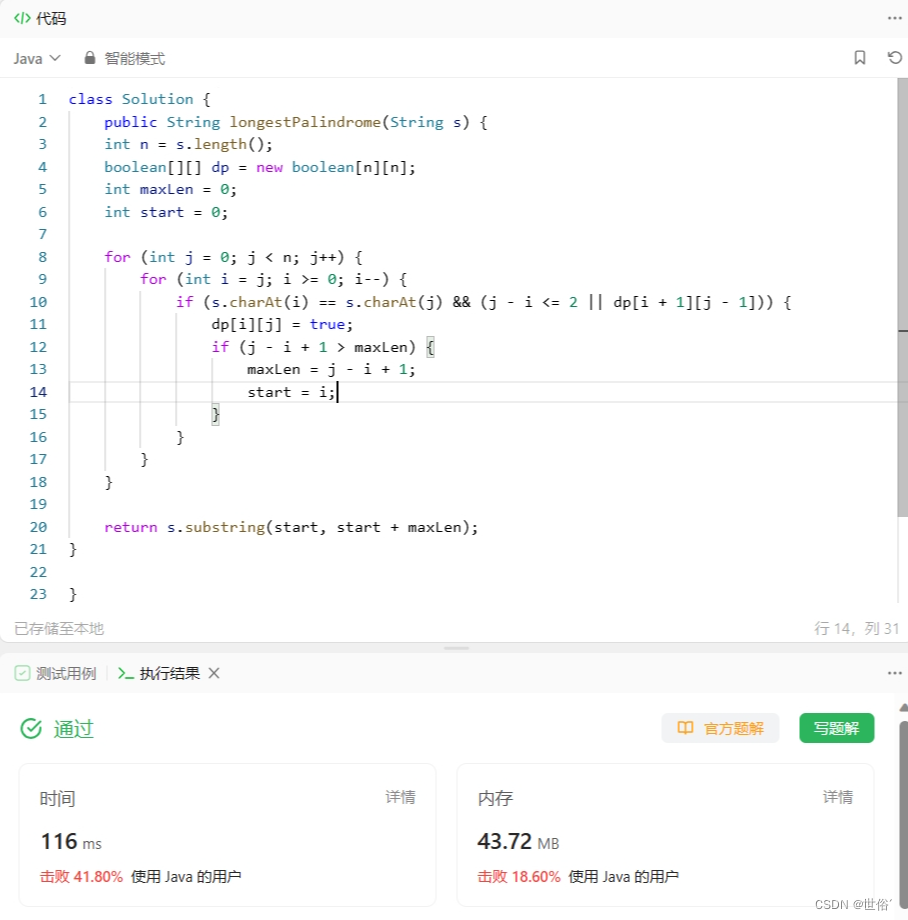
方法二：中心扩展法

除了动态规划方法外，还可以使用中心扩展法来解决这个问题。

中心扩展法的思路是，对于每个字符或每对相邻字符，以它们为中心向两边扩展，判断是否是回文串。具体步骤如下：

  1. 遍历字符串中的每个字符，将每个字符作为中心（回文串长度为奇数的情况）或相邻字符的中间位置（回文串长度为偶数的情况）。
  2. 在每个中心位置，使用双指针，从中心向两边扩展，判断左右的字符是否相等，直到无法再扩展为止。
  3. 在扩展过程中，记录并更新最长回文子串的起始索引和长度。
  4. 最后，根据最长回文子串的起始索引和长度，提取出最长回文子串。
class Solution {
   public String longestPalindrome(String s) {
    int n = s.length();
    int start = 0, maxLen = 0;

    for (int i = 0; i < n; i++) {
        // 中心为一个字符的情况
        int len1 = expandAroundCenter(s, i, i);
        // 中心为相邻字符的情况
        int len2 = expandAroundCenter(s, i, i + 1);
        int len = Math.max(len1, len2);

        if (len > maxLen) {
            maxLen = len;
            // 根据中心和回文串长度计算起始索引
            start = i - (len - 1) / 2;
        }
    }

    return s.substring(start, start + maxLen);
}

private int expandAroundCenter(String s, int left, int right) {
    while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
        left--;
        right++;
    }
    // 扩展的长度为 right-left-1，减1是因为不满足条件时left和right多移动了一步
    return right - left - 1;
}
}

该算法的时间复杂度为O(n^2)，空间复杂度为O(1)，其中n为字符串的长度。中心扩展法利用了回文串的特点，可以高效地找到最长回文子串。 

LeetCode运行结果：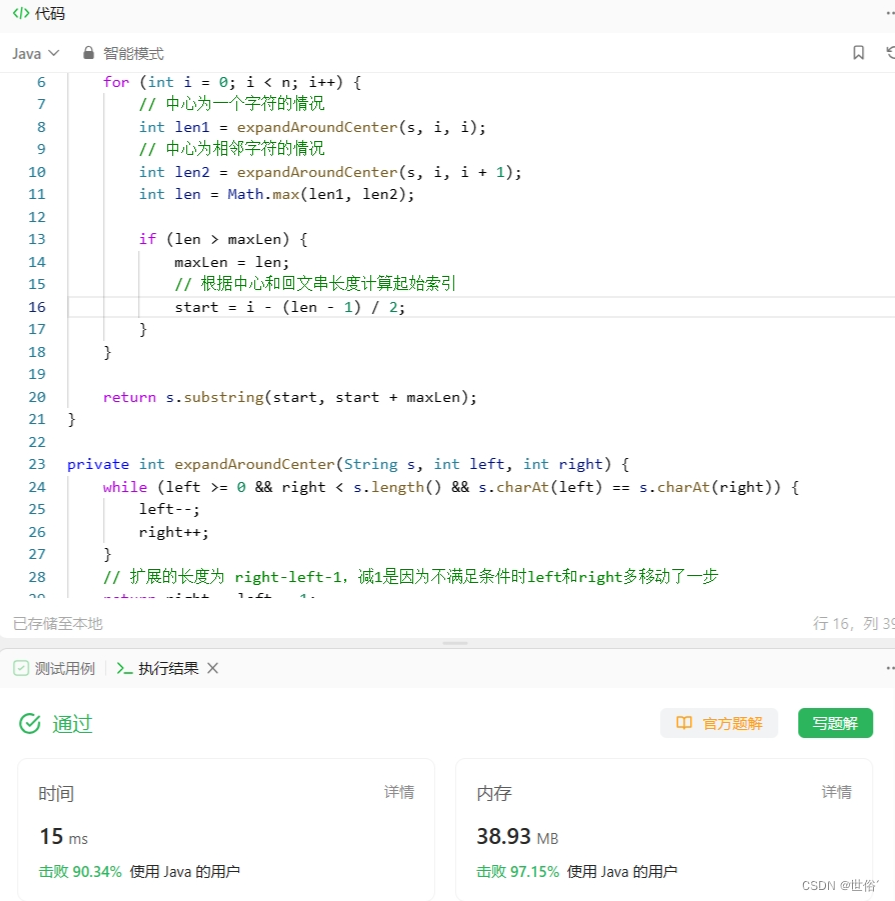

方法三：Manacher 算法

除了动态规划和中心扩展法之外，还有一种称为Manacher算法的线性时间算法可以用于查找最长回文子串。Manacher算法的核心思想是利用回文串的对称性，在遍历过程中尽量复用已经计算过的回文子串信息。

具体步骤如下：

  1. 首先，我们需要对原始字符串进行预处理，将其转换为一个新的字符串，这样可以将奇数长度和偶数长度的回文串统一处理。
    • 在每个字符前后添加特殊字符（例如#），以确保新字符串中的回文串长度都是奇数。
    • 在新字符串的开头和结尾添加特殊字符（例如$和%），以便处理边界情况。
    • 新字符串的长度将是原始字符串长度的两倍加一。
  2. 定义一个辅助数组P，其中P[i]表示以新字符串中索引i为中心的回文串的半径长度（包括中心字符在内）。
    • 使用两个变量center和right来维护当前已经找到的最右边界的回文串的中心和右边界。
    • 在遍历的过程中，逐个计算P[i]的值。
      • 当i在当前最右边界right的左侧时，使用对称性快速计算出初始猜测值，即P[i] = P[2 * center - i]。但如果该猜测值超出了最右边界，则需要修正为最右边界到边界之间的距离，即P[i] = right - i。
      • 然后，利用中心扩展法向两边扩展，直到无法再扩展为止，更新P[i]的值并更新最右边界。
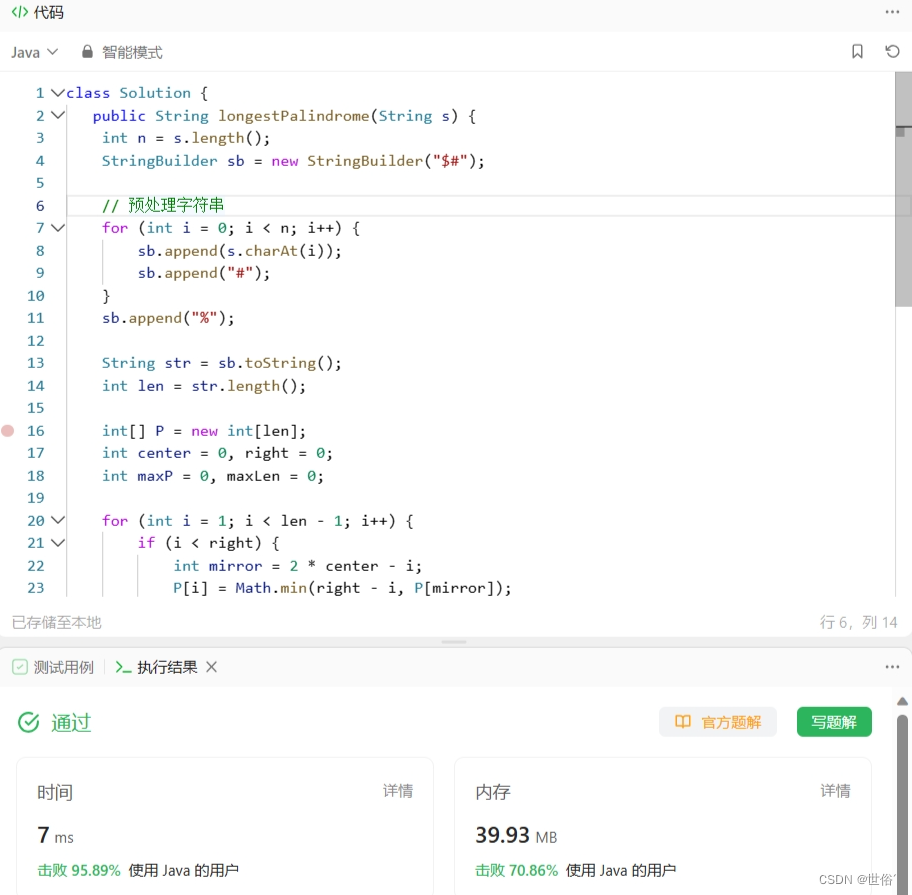
  3. 在遍历过程中，记录并更新最长回文子串的起始索引和长度。最长回文子串的长度即为maxLen = max(P) - 1，起始索引为start = (maxP - 1) / 2。
  4. 最后，根据最长回文子串的起始索引和长度，提取出最长回文子串。
class Solution {
   public String longestPalindrome(String s) {
    int n = s.length();
    StringBuilder sb = new StringBuilder("$#");

    // 预处理字符串
    for (int i = 0; i < n; i++) {
        sb.append(s.charAt(i));
        sb.append("#");
    }
    sb.append("%");

    String str = sb.toString();
    int len = str.length();

    int[] P = new int[len];
    int center = 0, right = 0;
    int maxP = 0, maxLen = 0;

    for (int i = 1; i < len - 1; i++) {
        if (i < right) {
            int mirror = 2 * center - i;
            P[i] = Math.min(right - i, P[mirror]);
        }

        // 中心扩展
        while (str.charAt(i + P[i] + 1) == str.charAt(i - P[i] - 1)) {
            P[i]++;
        }

        // 更新最右边界
        if (i + P[i] > right) {
            center = i;
            right = i + P[i];
        }

        // 记录最长回文子串的起始索引和长度
        if (P[i] > maxLen) {
            maxLen = P[i];
            maxP = i;
        }
    }

    int start = (maxP - maxLen) / 2;
    return s.substring(start, start + maxLen);
}
}

Manacher算法的时间复杂度为O(n)，空间复杂度为O(n)，其中n为字符串的长度。相比于动态规划和中心扩展法，Manacher算法在效率上具有优势，特别适用于处理大规模字符串。

LeetCode运行结果：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1014894.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

理解HTTPS/TLS/SSL（二）可视化TLS握手过程并解密加密数据

理解HTTPS/TLS/SSL（二）可视化TLS握手过程并解密加密数据

文章目录 WireShark抓包TLS握手过程Client HelloServer HelloEncryped Extenstions, Certificate, Certificate VerifyChange Ciper Spec, FinshedTLS 1.2和TLS 1.3的区别能不能在进一步&#xff1f; 解密WireShark中抓到的TLS包参考资料 上一篇文章已经在本地使用了生成自签名…
阅读更多...
从字符串中删除指定字符

从字符串中删除指定字符

任务描述 编写一个函数实现功能&#xff1a;从字符串中删除指定的字符。同一字母的大、小写按不同字符处理。例如&#xff1a;程序执行时输入字符串&#xff1a;turbo c and Borland c&#xff0c;从键盘输入字符n&#xff0c;则输出后变为&#xff1a;turbo c ad Borlad c。如…
阅读更多...
【openscreen 】FrameId

【openscreen 】FrameId

当前同步的最新版测试代码中用到了FrameId类 Frameid E:\chromium\src\media\cast\common\frame_id.h属于第三方库：openscreen E:\chromium\src\third_party\openscreen\src\cast\streaming\frame_id.h 为啥我感觉是int64的？ 支持+ <<
阅读更多...
【C#】FileInfo类 对文件进行操作

【C#】FileInfo类 对文件进行操作

提示&#xff1a;使用FileInfo类时&#xff0c;要引用System.IO命名空间。 using System.IO; FileInfo类 生成文件删除文件移动文件复制文件获取文件名判断文件是否存在属性列表其它常用方法 生成文件 Create()&#xff1a;在指定路径上创建文件。 FileInfo myFile new FileIn…
阅读更多...
我们一直谈论“写代码”，但你会“读代码”吗？

我们一直谈论“写代码”，但你会“读代码”吗？

编程&#xff0c;又被称作“写代码”&#xff0c;“敲代码”。 这个说法有可能会带来一点点误解&#xff0c;让人觉得如何“写”是学习编程要解决的主要问题。但事实并非如此。尽管最终代码要在键盘上敲出来&#xff0c;但这个过程在开发中的实际时间占比可能要远远小于你的预…
阅读更多...
算法通过村第七关-树(递归/二叉树遍历)青铜笔记|手撕递归

算法通过村第七关-树(递归/二叉树遍历)青铜笔记|手撕递归

文章目录 前言1. 递归的特征2. 如何写出好的递归3. 怎么看懂递归的代码总结 前言 提示&#xff1a;我们生活在24小时不眠不休的社会里但是没有24小时不眠不休的身体有些东西必须舍弃 -- 马特海格 这一关&#xff0c;我看要谈论的是递归问题&#xff0c;说到它就牵扯到很多问题了…
阅读更多...
QT基础教学(QT对象间的关系)

QT基础教学(QT对象间的关系)

文章目录 前言一、QT间的父子关系二、聚合关系三、组合关系四、关联关系五、依赖关系总结 前言 本篇文章我们来讲解QT对象间的关系&#xff0c;理清楚QT对象间的关系是非常重要的&#xff0c;没有理清楚QT间的对象关系可能会导致内存的泄漏等各种问题的出现。 资料合集地微信…
阅读更多...
HarmonyOS开发：那些开发中常见的问题汇总（一）

HarmonyOS开发：那些开发中常见的问题汇总（一）

前言 本来这篇文章需要讲述静态共享包如何实现远程依赖和上传以及关于静态共享包私服的搭建&#xff0c;非常遗憾的告诉大家&#xff0c;由于组织管理申请迟迟未通过&#xff0c;和部分文档官方权限暂未开放&#xff0c;关于这方面的讲解需要延后了&#xff0c;大概需要等到202…
阅读更多...
HeyFriday AI：智能AI写作工具

HeyFriday AI：智能AI写作工具

【产品介绍】​ 名称 HeyFriday AI 具体描述​ HeyFriday是一款智能AI写作工具&#xff0c;可以帮助用户快速生成博客、广告、创意故事等各种类型的文本内容&#xff0c;节省时间和金钱。​HeyFriday的团队由前谷歌NLP科学家&#xff08;ALBERT的第一作者&#xff…
阅读更多...
VIRTIO-BLK代码分析（5）virtqueue通信

VIRTIO-BLK代码分析（5）virtqueue通信

virtqueue用于VIRTIO驱动和VIRTIO设备进行通信。每个VIRTIO设备可能有一个或多个virtqueue&#xff0c;VIRTIO-BLK的virtqueue数目可以通过num_queues设置。 通过函数vring_create_virtqueue创建virtqueue&#xff0c;通过函数virtqueue_add_sgs添加数据。目前存在split virtqu…
阅读更多...
【网络编程】UDP Socket编程

【网络编程】UDP Socket编程

UDP Socket编程 一. DatagramSocket二. DatagramPacket三. InetSocketAddress四. 执行流程五. 代码示例: UDP 回显服务器 数据报套接字&#xff1a; 使用传输层 UDP 协议 UDP: 即 User Datagram Protocol&#xff08;用户数据报协议&#xff09;&#xff0c;传输层协议。 UDP…
阅读更多...
Jmeter系列-定时器Timers的基本介绍（11）

Jmeter系列-定时器Timers的基本介绍（11）

简介 JMeter中的定时器&#xff08;Timer&#xff09;是一种重要的元件&#xff0c;用于模拟用户在不同时间间隔内发送请求的场景。通过使用定时器&#xff0c;可以模拟负载、并发和容量等不同情况下的请求发送频率。 使用定时器 可以在取样器下添加定时器&#xff0c;这样定…
阅读更多...
机器学习第五课--广告点击率预测项目以及特征选择的介绍

机器学习第五课--广告点击率预测项目以及特征选择的介绍

这个项目的主要的目的是通过给定的广告信息和用户信息来预测一个广告被点击与否。 如果广告有很大概率被点击就展示广告&#xff0c;如果概率低&#xff0c;就不展示。 因为如果广告没有被点击&#xff0c;对双方&#xff08;广告主、平台&#xff09;来讲都没有好处。所以预测…
阅读更多...
应用商店优化之关键词优化指南1

应用商店优化之关键词优化指南1

提高我们应用在应用商店中的知名度&#xff0c;完全取决于关键词。找到一些关键词的策略之后&#xff0c;我们应该选择最有前途的关键词并对其进行研究&#xff0c;从而创建新的组合和长尾关键词。 1、寻找关键词&#xff0c;找到一些潜在的关键词创意。 尝试考虑一下我们将如…
阅读更多...
Element表格之表头合并、单元格合并

Element表格之表头合并、单元格合并

一、合并表头 el-table配置 :header-cell-style"headFirst"headFirst({ row, colunm, rowIndex, columnIndex }) {let base { background-color: rgba(67, 137, 249, 0.3), color: #333, text-align: center };//这里为了是将第一列的表头隐藏&#xff0c;就形成了合…
阅读更多...
Python开发环境配置

Python开发环境配置

Python 作为一个语言&#xff0c;代码需要一个解释器来进行解释&#xff0c;这个解析器就是专门针对 Python 代码的&#xff0c;只有它才知道这些代码是什么意思。编写代码也需要一定的工具&#xff0c;理论上所有的纯文本都可以编写代码&#xff0c;但工欲善其事必先利其器&am…
阅读更多...
Python 办公自动化之 PDF 操作详解

Python 办公自动化之 PDF 操作详解

1、PyMuPDF简介 1. 介绍 在介绍PyMuPDF之前&#xff0c;先来了解一下MuPDF&#xff0c;从命名形式中就可以看出&#xff0c;PyMuPDF是MuPDF的Python接口形式。 MuPDF MuPDF 是一个轻量级的 PDF、XPS和电子书查看器。MuPDF 由软件库、命令行工具和各种平台的查看器组成。 M…
阅读更多...
安卓修改rom 移植rom必备常识 lib--**so文件基本解析

安卓修改rom 移植rom必备常识 lib--**so文件基本解析

安卓系统lib-so文件 解包安卓固件中lib lib64分区下存在很多后缀为so的文件&#xff0c;其实都是系统的动态库&#xff0c;类似于win下面的*.dll&#xff0c;一般是由C/C编译成的动态库.在系统lib的文件夹下&#xff0c;置换移植其他系统的程序也需要修改更换相关so文件.没有它…
阅读更多...
Android---底部弹窗之BottomSheetDialog

Android---底部弹窗之BottomSheetDialog

BottomSheetDialog 是Android开发中的一个弹出式对话框&#xff0c;它从屏幕底部弹出并覆盖部分主界面。 1. BottomSheetDialog的使用 // 参数2&#xff1a;设置BottomSheetDialog的主题样式&#xff1b;将背景设置为transparent&#xff0c;这样我们写的shape_bottom_sheet_…
阅读更多...
C【函数】

C【函数】

1.常用API 1.strcpy&#xff1a;#include<string.h> char * strcpy ( char * destination, const char * source );int main(){char arr1[] "bit";char arr2[20] "###########";// bit\0########strcpy(arr2, arr1);printf("…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023