---

前言

---

提示：我们生活在24小时不眠不休的社会里但是没有24小时不眠不休的身体有些东西必须舍弃 -- 马特·海格

这一关，我看要谈论的是递归问题，说到它就牵扯到很多问题了

1. 与树和二叉树的相关问题
2. 二分查找相关问题
3. 快速排序和并轨排序问题
4. 回溯问题
5. 动态规划问题

这一切都是递归算法为基础的，当然这一关也是必须掌握的。

1. 递归的特征

递归，大部分都知道是怎么回事，但是就是写不出代码来，此所谓“你讲的都对，但是我就不会”，递归的本质仍是方法的调用，不过是自己调用自己搞，系统给我们维护了不同调用之间的保存和返回的功能。

比如这个故事：

从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事，故事讲的是从前有座山，山上有座庙，庙里有个老和尚，老和尚在给小和尚讲故事······

---

如果看递归的结构，就像下面的这个样子，前面的一层取一摸一样的调用下一层，不同的只是输入和输出参数，这个递归过程是写递归的一个核心问题。

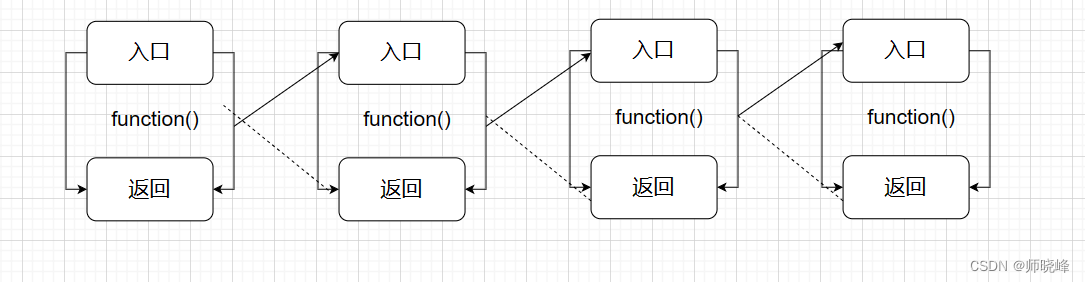
当然这个过程不能一致持续下去，一定要在满足某个要求之后返回结果，否则的话就会抛出我们常见的“StackOverFlow”的问题。

所有的递归有两个必要的特征：

1. 执行时范围不断缩小，这样才能触底反弹
2. 种植判断在调用递归的前面

理解这个,是我们掌握递归的辅助工具，我们一一分析：

• 执行范围不断缩小

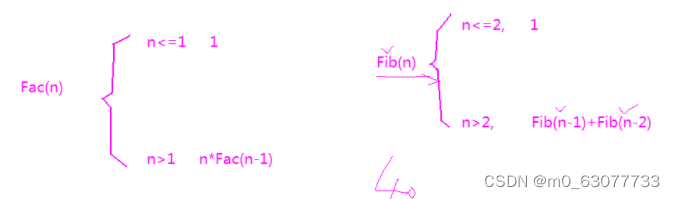
递归在数学里的概念是递推，设计递归就是努力寻找数学里的递推公式。经典的问题就是求阶乘，好多同学也是通过这个认识递归的吧，那时我们第一次见面。 还记得递推公式吗？ f(n) = f(n-1) * n,很显然一定是触底之后才能反弹的，再比如就是典型的斐波那契数列递推公式了，f(n) = f(n -1) + f(n - 2);当然n也是在不断的缩小。这条规律可以辅助我们检查自己写的递推公式对不对。

再比如后面我们会遇到青蛙跳台阶问题，他的递推公式f(n) = f(n -1) + f(n - 2);你想奇怪呀？怎么会一样呢，没错，他就一样🤣。

范围缩小不一定只体现在n的变化上，在树的递归中，我们会大量的接触到类似这样的结构：

int leftDepth = getDepth(node.left); // 左
int rightDepth = getDepth(node.right); // 右

每一次递归，都是在将范围缩小到当前节点的左子树或者右子树，范围也是在不断的缩小的。

• 终止条件判断在递归调用的前面

递归之后可能还有终止条件，但是在执行递归之前，一定会有一个终止条件。这个条件可以帮助我么你检查自己写的算法对不对。

为什么呢？我们看个例子🌰：

很显然recursion()会不断的调用自己，这样一直递归下去，就无法退出来，知道抛出堆栈溢出异常（StackOverFlowError)。

public void recursion(参数0) {
    recursion(参数1)；
    if(终止条件) {
        return ；
	}
}

所以：任何递归方法在执行之前，一定会有一个终止条件

实际上一个方法里的递归调用可能不止一次，还会加一些逻辑处理，比如下面这样，但是终止的条件仍然在前面。

public void recursion(参数0) {
    if(终止条件) {
        return ；
	}
        // 逻辑一
        recursion(参数1)；
        // 逻辑二
        recursion(参数2)；
        // ......
        recursion(参数n)；
        可能还有其他一些逻辑运算
}

这一特点启示我们，可以先考虑在什么条件下终止，而相关代码要写在靠前的位置，之后再考虑递归的逻辑，这样可以很好的降低编写代码的难度。

2. 如何写出好的递归

明白了上面的道理，那么你就右疑问了，怎么写出好的递归方法呢？

• 从小到大递推

递归该怎么写？递归源于数学里的归纳法，这个在高中数学里面有的。大致呢？你先猜出存在的递归关系，f(n) = pf(n-1)，然后你只要证明当n增加1时，f(n + 1) = pf(n)也是成立的就说明你的猜想没有问题。不过在算法里面，我们写递归一般不需要证明，我么你先挑选几个较小的值验证一下，然后再选择几个较大的值验证一下就可以了。

很显然大部分从n = 1,2,3或者只有一两个元素开始写最简单。典型的就是斐波那契数列为 1 1 2 3 5 8 …，从 n = 3开始都满足f(n) = f(n - 1) + f(n -2)，然后我们再选择某个比较大的n来验证就可以了。

所以-这就是我们要找的递推公式：

f(n) = f(n - 1) + f(n -2)

对于阶乘来说也一样

n == 1 f(1) = 1
n == 2 f(2) = 2 * f(1) = 2
n == 3 f(3) = 3 * f(2) = 6
n == 4 f(4) = 4 * f(3) = 24
...

由此我们可以推测递推公式：f(n) = n * f(n - 1)。

• 分情况讨论，明确结束条件

我们说过递归里面的终止条件一定时靠前的，而大部分递归的终止条件不是n最小开始出低反弹时有几种情况：

对于阶乘，当n == 1 时你就知道f(1) = 1,也就是下面这个样子：

// 算 n 的阶乘（假设n ！= 0）
int f(n) {
	if(n == 1){
        return 1;
	}
}

有时候要考虑的终止条件不知一个，例如斐波那契数列的递推公式f(n) = f(n -1) + f(n - 2)里面，如果n = 2 即 f(2) = f(1) + f(0)，很显然这里面没有f(0)，所以我们也要将 n == 2 也给限制住，所以结果就变成如下这样：

int f(n) {
	if(n <= 2){
        return 1;
	}
}

有些情况不一定触底才开始反弹，而是达到某种要求就要停止，这样需要考虑的情况会比较多。解决这类问题最直接的方法就是枚举，可以将所有情况列举出来，然后再一一去优化。

只有列举清楚了才可能将终止条件写完整，所以在面试的情况下，不要上来就写，而是和面试官讨论你的设计方案，不要害怕和面试官讨论，假如有很明显的缺陷他也甚至提醒你一下，所以这也是一个借力打力的一个技巧。

确定终止条件队递归至关重要，后面很多题目会话很大的篇幅来分析怎么判断终止条件，一旦判断完毕，递推关系就是水到渠成了。

• 组合成完整的方法

将递推公式和终止条件组合起来，变成完整的方法。

递归经常能看出很多骚操作代码，不要迷信呀，分情况逐个先写出来，之后再看看能否精简优化，不要一个步子迈得太大，容易出事故。我们还是那上面的例子举例，完善我们的代码：

// 算 n 的阶乘（假设n ！= 0）
int factorial(n) {
	if(n == 1){
        return 1;
	}
    rerurn n * factorial(n - 1);
}

// 斐波那契数列
int factorial(n){
	// 1. 先写递归结束条件
	if(n <= 2){
        return 1;
	}
	// 2. 接着写等价关系式
   return factorial(n - 1) + factorial(n - 2);
}

每次写递归，都要多方面考虑，后面我们写的时候要注意。

入参和出参？？埋坑

3. 怎么看懂递归的代码

对很多人来说，递归最大的问题在于给了答案，看不懂代码，而递归的代码也贼难调试，其实一个转换一下思路就很好解决了。

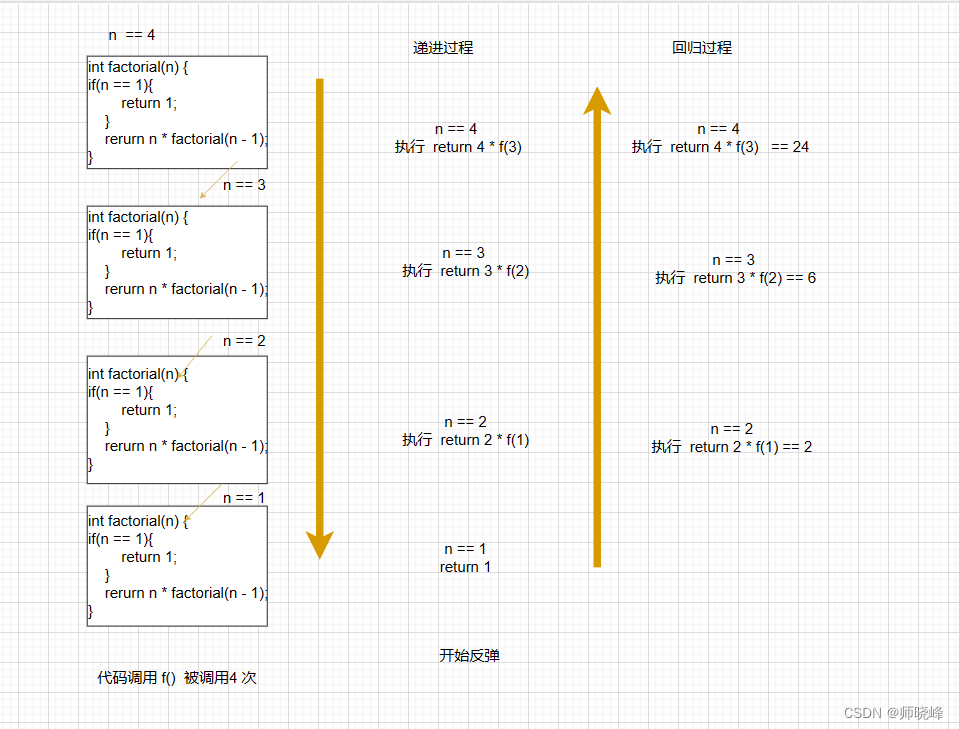
我们先思考一个问题，上面的阶乘，如果n == 4 ，调用了几次上面的f()方法呢？很显然是4次。这个就是递归的一个特征【不撞南墙不回头】，n == 4，3，2是会继续递归，知道有1是满足条件退出，然后就return 1，不再递归了，而且是不断返回上一层并计算。

接着再看返回时每层参数的问题，递归本质上仍然是方法调用，所以可以按照方法调用的方式来检验写的对不对。

下面是一个完整的思路，你会发现递归不归是一个方法被调用了好几次，而每次n都在减小，这就是递归的过程，触底之后，也就是满足终止条件后就开始返回了。

递归的时候当前层的n被系统给保存，而返回的时候会自动设置会来，一次每层n是不一样的，所以就是重新拿到当前这一层n的值完成计算即可。

f(4)阶乘的过程如下：

---

总结

提示：递归思路，递归的图解，怎么写好递归