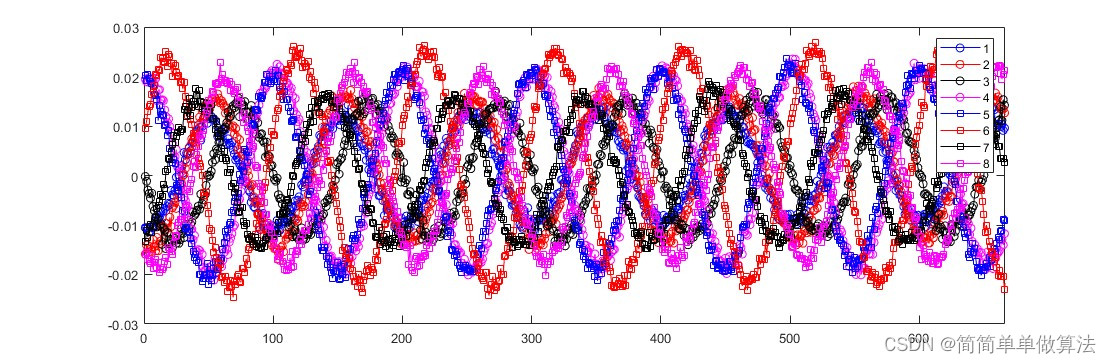
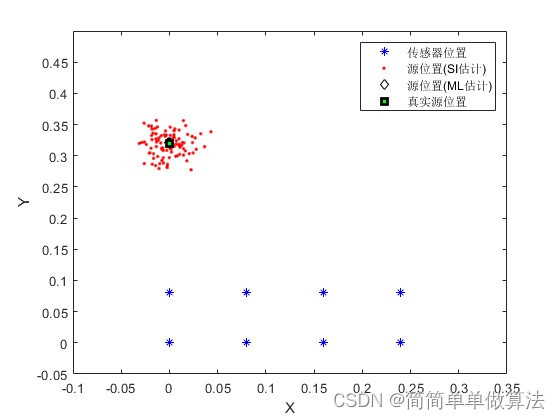
1.算法运行效果图预览

2.算法运行软件版本

matlab2022a

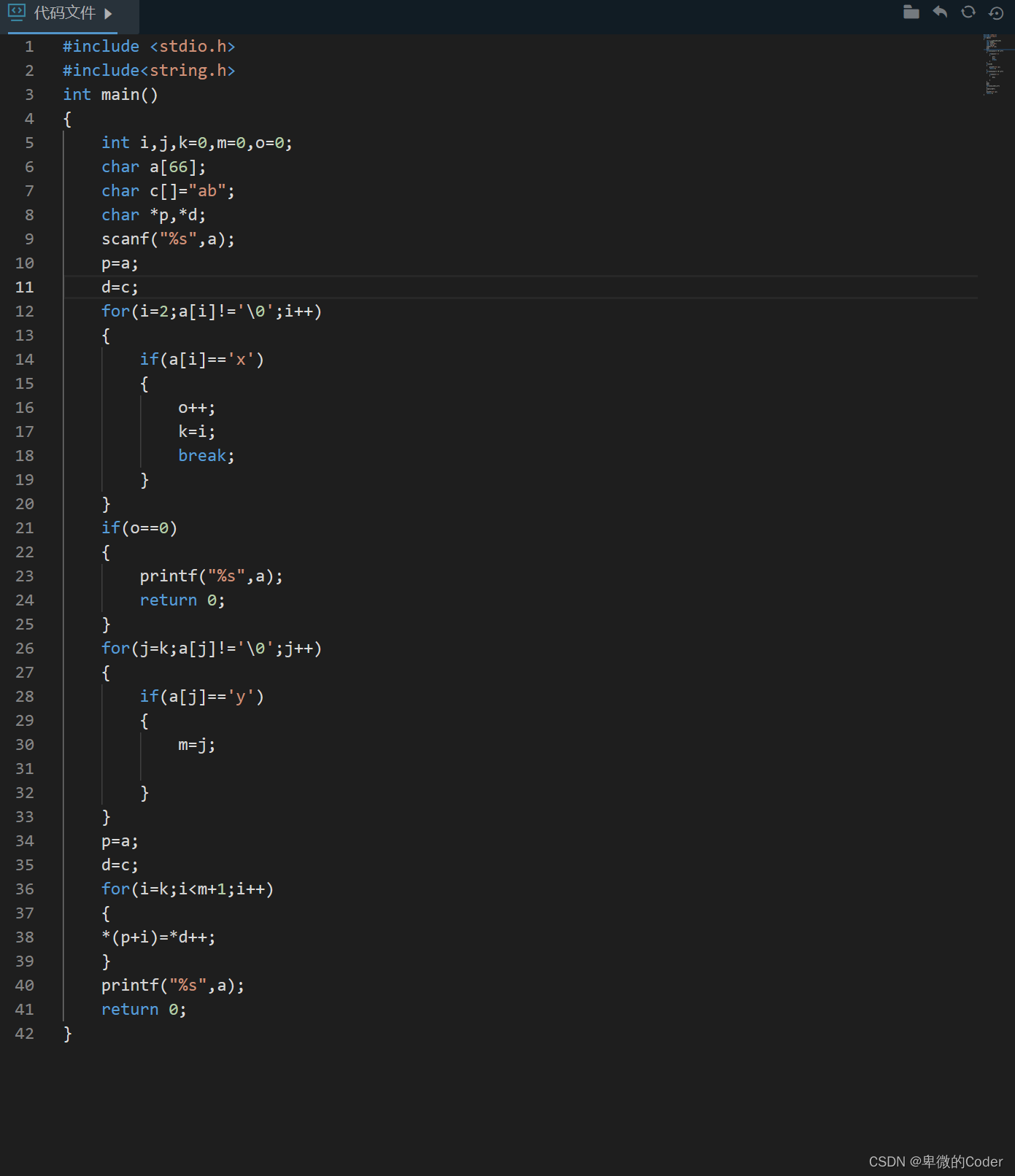
3.部分核心程序

....................................................................
%ML
if (bML==1)
    varxs_ML=var(bias_Xs_ML(:,1)); 
    varys_ML=var(bias_Xs_ML(:,2)); 
    varrs_ML=var(bias_Rs_ML); 
    varbear_ML=var(bias_bearing_ML);

    vect_var_ML=[varxs_ML;varys_ML;varrs_ML;varbear_ML]; 
end

% Calculate second moment (RMS)= sqrt {E[a^2]} = sqrt {mean^2 + variance} 
% ----------------------------------------------------- 
rmsxs_SI=sqrt(mean(bias_Xs_SI(:,1)).^2+varxs_SI); 
rmsys_SI=sqrt(mean(bias_Xs_SI(:,2)).^2+varys_SI); 
rmsrs_SI=sqrt(mean(bias_Rs_SI).^2+varrs_SI); 
rmsbear_SI=sqrt(mean(bias_bearing_SI).^2+varbear_SI);

vect_rms_SI=[rmsxs_SI;rmsys_SI;rmsrs_SI;rmsbear_SI];

%ML
if (bML==1) 
    rmsxs_ML=sqrt(mean(bias_Xs_ML(:,1)).^2+varxs_ML); 
    rmsys_ML=sqrt(mean(bias_Xs_ML(:,2)).^2+varys_ML); 
    rmsrs_ML=sqrt(mean(bias_Rs_ML).^2+varrs_ML); 
    rmsbear_ML=sqrt(mean(bias_bearing_ML).^2+varbear_ML);

    vect_rms_ML=[rmsxs_ML;rmsys_ML;rmsrs_ML;rmsbear_ML]; 
end
......................................................................
fisher=jacobian'*inv(cov_mat)*jacobian;

crlb= trace(fisher^-1); % compare with MSE of Rs

% ----------------------------------------------------- 
% Generate Plots
% -----------------------------------------------------

% hfig1=figure;
if (bML==1)
plot(xi, yi,'b*',Xs_SI(:,1), Xs_SI(:,2),'r.',Xs_ML(:,1), Xs_ML(:,2), 'kd'); % plot both SI and ML
hold on
plot(xs_src_actual, ys_src_actual,'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',6); % plot both SI and ML

else
plot(xi, yi,'bv', xs_src_actual, ys_src_actual, 'r^', Xs_SI(:,1), Xs_SI(:,2), 'mo'); % plot just SI only
end

 
if (bML==1)
legend('传感器位置', '源位置(SI估计)','源位置(ML估计)','真实源位置' );
else
legend('传感器位置', '真实源位置', '源位置(SI估计)');
end


xlabel('X'); 
ylabel('Y');
 
axis([-0.1,0.35,-0.05,0.5]);
36_004m

4.算法理论概述

Levenberg-Marquardt 算法是求非线性最小二乘问题的一种优化算法。它在不需要二阶导数信息的情况下，仍然可以取得相当不错的优化效果。它对于具有强非线性性和高维度的问题，尤为适用。

Levenberg-Marquardt 算法是在高斯-牛顿法和梯度下降法之间寻求一种折中的优化算法。在每一步迭代中，它使用高斯-牛顿法的近似 Hessian 矩阵，但是加上一个引入松弛性质的调节因子，这样可以大幅度减少病态问题的发生。同时，Levenberg-Marquardt 算法也采用了梯度下降法的思想，在 Hessian 矩阵无法更新或者接近于无法更新的时候，使用梯度下降法继续迭代。

Levenberg-Marquardt 算法的本质是在求解非线性最小二乘问题中，将误差平方和作为代价函数，找到一种参数的集合，使得该代价函数最小。在每一步迭代中，它通过计算代价函数的一阶导数和二阶导数，更新参数的值。对于 Hessian 矩阵接近奇异矩阵或者代价函数停滞不前的情况，它通过调节因子来提高二阶导数的稳定性。同时，为了防止过拟合，Levenberg-Marquardt 算法还采用了正则化的方法，用来处理噪声和异常点。

声源定位是一种通过声音来确定其来源的技术。它广泛应用于语音识别、音频信号处理、机器人听觉、生物医学影像处理等领域。

在声源定位中，基于Levenberg-Marquardt算法是一种常用的优化方法，它主要用于求解非线性最小二乘问题。其基本原理是通过迭代来优化目标函数，直到达到最优解。

一、Levenberg-Marquardt算法的基本原理

Levenberg-Marquardt算法是一种迭代方法，用于求解非线性最小二乘问题，它通过最小化目标函数与已知数据之间的差异来定位声源。

其基本原理是将目标函数与已知数据之间的差异定义为残差，然后通过迭代来最小化残差。在每次迭代中，根据当前估计的参数值，计算出残差的梯度，然后使用该梯度来更新参数。

Levenberg-Marquardt算法的优点在于它能够处理非线性问题，同时避免了大量的矩阵计算，因此适用于实时声源定位系统。

其基本原理如下：