一、算法思路
K近邻算法,k-nearest neighbor,即K-NN
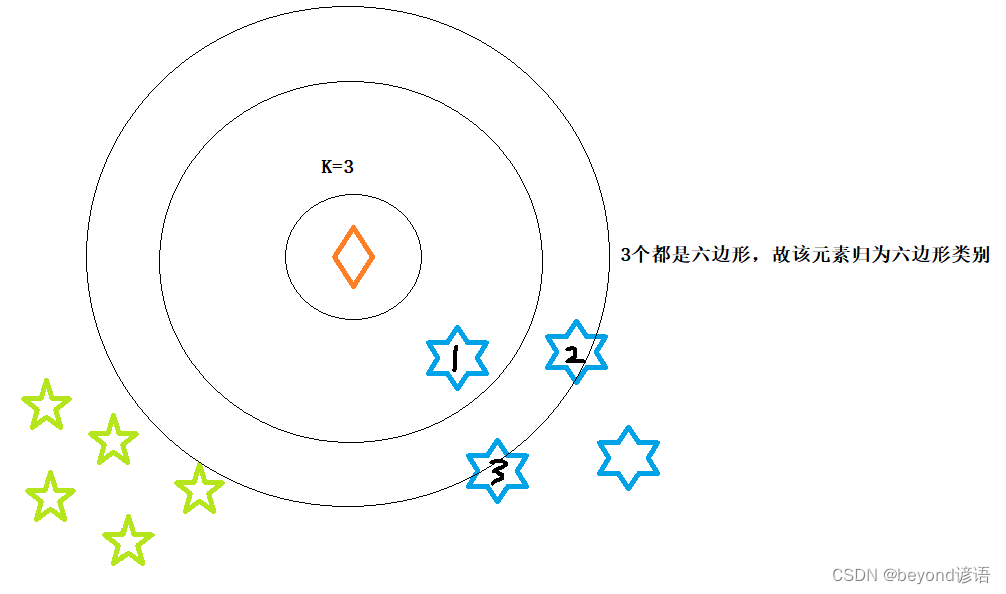
通俗来说:给定一个元素,然后以该元素坐标为圆心开始画圆,其中K值是超参数需要人为给定,圆的半径逐渐增大(距离度量采用欧氏距离),直到包含其他K个元素为止,然后看所包含的K个元素都属于哪些类别,根据决策规则(采用少数服从多数原则),看K个元素属于哪些类别多,那么x就归为哪类。
应用场景:已知有两个类别绿色五边形和蓝色六边形,新加入一个橙色元素x,问x可归为哪一类?
1,三要素
距离度量、K值、决策规则
①距离度量
空间中,距离越近的元素越容易是同一个类别,因为其相似度较高。
距离度量方法很多,常用的有欧式距离、曼哈顿距离、余弦距离等
Ⅰ、欧氏距离
两点之间距离公式: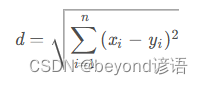
当然可以是更高维度的距离,同样道理计算方法都一样,高维度也可以应用。
Ⅱ、曼哈顿距离
两个点在坐标系上的绝对轴距总和: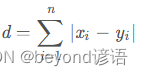
Ⅲ、余弦距离
向量空间中两个向量夹角的余弦值: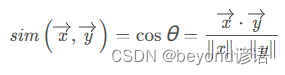
距离度量目的是看未知元素与哪个已存在的类别最近,那么新来的元素就可以归为这类
②K值
K值可以理解为结束条件,是个超参数,需要人为给定
不同的K值最终算法表现出来的效果也不尽相同,甚至可以会差异很大
通常使用交叉验证的方法来确定最优K值
③决策规则
常见的决策规则有:少数服从多数原则、加权平均原则等
Ⅰ、少数服从多数
这个很容易了解,比如K个元素,看哪个出现的类别多,那么新来的元素就是这个类别
Ⅱ、加权平均
这种情况提前是所有的类别均有对应的权值,将K个元素所对应的类别权重相加取平均,看该值离哪个类别权重值最近,就归为这个类别