1462. 课程表 IV

题目描述：

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你必须先选 ai 课程。

有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是间接的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

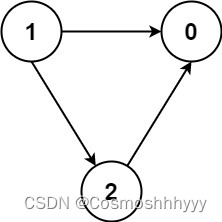
输入：numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

提示：

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
每一对 [ai, bi] 都不同
先修课程图中没有环。
1 <= queries.length <= 104
0 <= ui, vi <= n - 1
ui != vi

实现代码与解析：

拓扑排序

class Solution {
public:
    // 邻接表
    vector<int> e = vector<int>(5010, 0), ne = vector<int>(5010, 0), h = vector<int>(110, -1);
    int idx = 0;

    // 加边
    void add (int a, int b)
    {
        e[idx] = b, ne[idx] = h[a], h[a] = idx++;
    }

    vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
        vector<vector<bool>> sumres(numCourses, vector<bool>(numCourses));
        vector<bool> res;
        vector<int> indeg(numCourses, 0);

        for (auto t: prerequisites)
        {
            add(t[0], t[1]);
            indeg[t[1]]++; // 入度++
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++)
        {
            if (indeg[i] == 0) q.push(i); // 度为 0 入队
        }

        // bfs
        while (q.size())
        {
            int t = q.front();
            q.pop();

            for (int i = h[t]; ~i; i = ne[i])
            {
                int j = e[i];
                sumres[t][j] = true; // 直接相连true

                indeg[j]--; // 入度--
                if (indeg[j] == 0) q.push(j);

                for (int k = 0; k < numCourses; k++)
                    sumres[k][j] = sumres[k][t] || sumres[k][j]; // 传递， 间接相连

            }
        }

        for (auto t: queries)
        {
            res.push_back(sumres[t[0]][t[1]]);
        }
        return res;
    }
};