高斯信号的贝叶斯步长最小均方算法（Matlab代码实现）

news2024/11/24 10:52:41

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

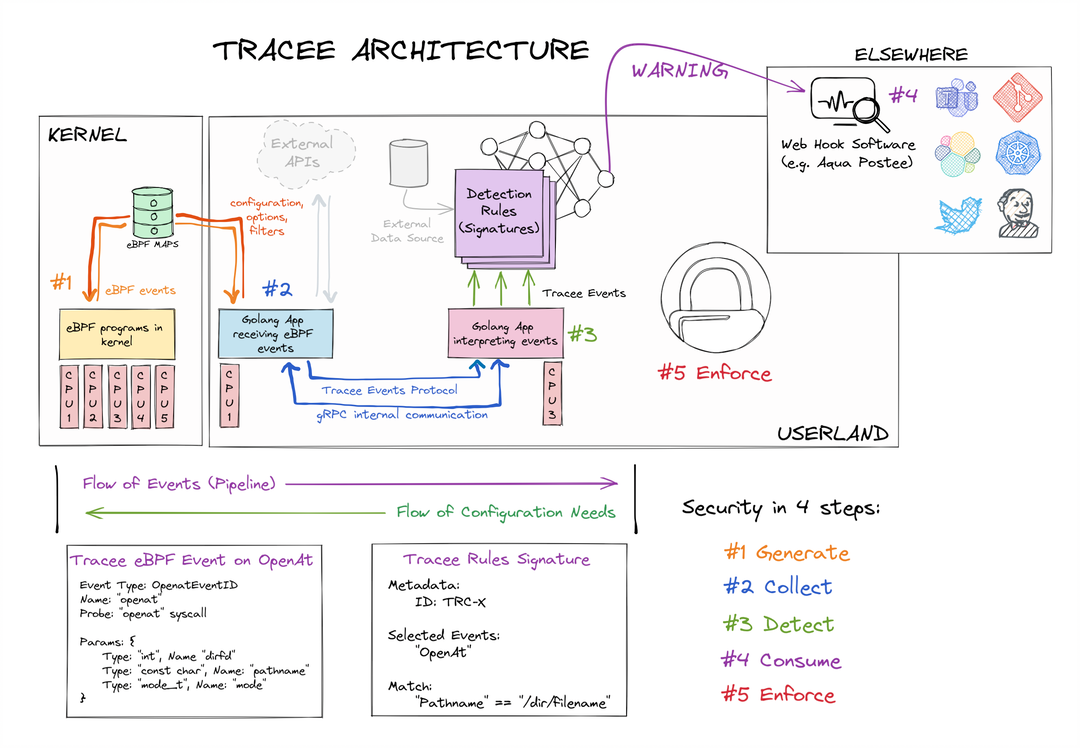
💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

LMS算法具有时变步长，在某些情况下可以证明其大小等效于卡尔曼滤波器。只要仔细选择卡尔曼滤波器的状态噪声和LMS算法的步长即可。卡尔曼滤波器是给定状态和测量噪声协方差矩阵的最佳线性估计器（贝叶斯），但这些矩阵并不总是已知的。这封信考虑了这些矩阵未知的情况，在卡尔曼滤波器简化为 LMS 的特殊情况下。这会导致一种算法选择具有很少先验的 LMS 算法的步长。最佳步长可以使用系数估计（qw）和测量噪声方差（qv）的概率密度函数（PDF）的估计值来计算。可以使用贝叶斯规则并假设高斯参考和测量噪声信号从数据中估计 PDF。经过一些近似，确定qw和qv的结果算法是第二个小卡尔曼滤波器。

📚2 运行结果

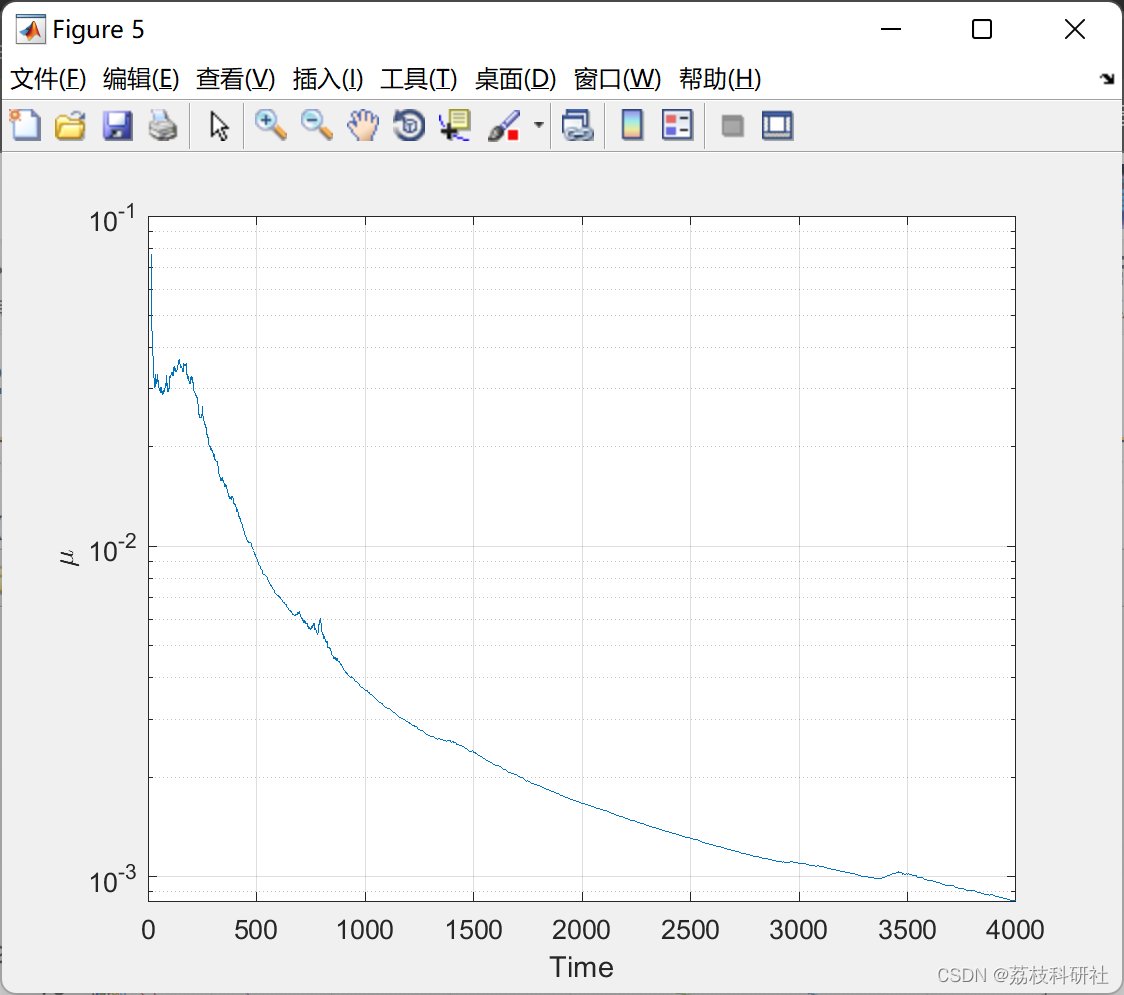
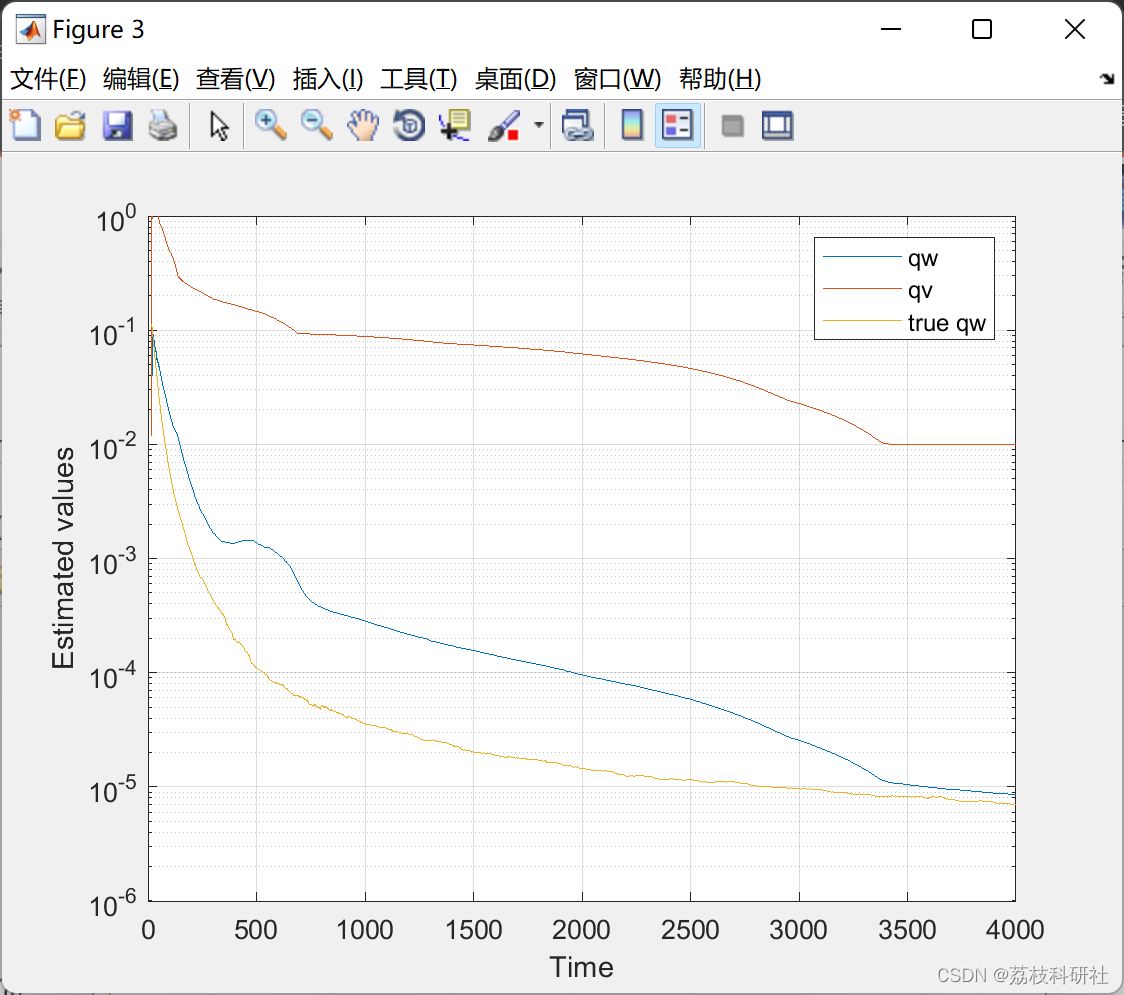
部分代码：

function [w, qo, A, b, mu] = BSLMS(uv, d, w, qo, A, b, N, alpha, max_trace_A, k)

% constants
delta = 1e-9; % a very small number close to the mantissa precision
ddelta = 1e-99; % a very very small number close to the floating-point precision

e = d - uv'*w;

%%%%%% q measure update

PT = uv'*uv + ddelta;
P = PT/N;
a = [PT, 1]';

inv_zeta_sq_times_2 = 1/(2*(a'*qo)^2 + ddelta);

A = A + inv_zeta_sq_times_2*(a*a');
b = b + inv_zeta_sq_times_2*e^2*a;

qo = (A+(ddelta+delta*trace(A))*eye(2)) \ b;

xi = b'*qo;
c = b/xi;
nx = 4*xi/k;

z = qo(1)/(qo(1)*PT+qo(2));
if z < 0
z = 0;
end
if z > 1/PT
z = 1/PT;
end

%%%%%% Calculation of mu=E[z]

if nx <= 4
mu = z;
else
% first derivative
d1 = ...
-(nx*(pi*z*(A(1,1) - 2*PT*A(1,2)) + pi*(z*A(1,1) - 2*(-1 + PT*z)*A(1,2)) + ...
2*pi*PT*(-1 + PT*z)*A(2,2)))/...
(4.*(pi*z*(z*A(1,1) - 2*(-1 + PT*z)*A(1,2)) + pi*power(-1 + PT*z,2)*A(2,2))) + ...
((-4 + nx)*(c(1) - PT*c(2)))/(2.*(z*c(1) + c(2) - PT*z*c(2)));

% second derivative
d2 = ...
-((-4 + nx)*power(c(1) - PT*c(2),2)*power(z*c(1) + c(2) - PT*z*c(2),-2))/2. + ...
(nx*power(pi*z*(A(1,1) - 2*PT*A(1,2)) + pi*(z*A(1,1) - 2*(-1 + PT*z)*A(1,2)) + ...
2*pi*PT*(-1 + PT*z)*A(2,2),2)*power(pi*z*(z*A(1,1) - 2*(-1 + PT*z)*A(1,2)) + ...
pi*A(2,2)*power(-1 + PT*z,2),-2))/4. - ...
(nx*(2*pi*(A(1,1) - 2*PT*A(1,2)) + 2*pi*A(2,2)*power(PT,2))*...
power(pi*z*(z*A(1,1) - 2*(-1 + PT*z)*A(1,2)) + pi*A(2,2)*power(-1 + PT*z,2),-1))/4;

if d2 >= 0
mu = 1/(2*PT); % at the middle of the interval
else

z0 = z - d1 / d2; % z0 is approximately equal to z at the maximum
pz = - d2; % 1/pz is the gaussian variance

ax = sqrt(pz)*(1-z0*PT)/(sqrt(2)*PT);
bx = z0*sqrt(pz)/sqrt(2);

if ax+bx < 1e-9 % the denominator is very small
mu = 0; % lim a -> -b
elseif abs(ax) > 10 && abs(bx) > 10 ...
&& sign(ax)<0 && sign(bx)>0 % erfc saturates at 0
mu = z0 + (-2+2*exp(-bx^2+ax^2))/...
(sqrt(2*pi*pz)*(...
-exp(-1/(2*ax^2))/(sqrt(pi)*ax)+...
-exp(-bx^2+ax^2-1/(2*bx^2))/(sqrt(pi)*bx)));
% erfc(x) +-= exp(-x^2-1/(2x^2))/(sqrt(pi)*x)
elseif abs(ax) > 10 && abs(bx) > 10 ...
&& sign(ax)>0 && sign(bx)<0 % erfc saturates at 0
mu = z0 + (-2*exp(bx^2-ax^2)+2)/...
(sqrt(2*pi*pz)*(...
-exp(bx^2-ax^2-1/(2*ax^2))/(sqrt(pi)*ax)+...
-exp(-1/(2*bx^2))/(sqrt(pi)*bx)));
% erfc(x) +-= exp(-x^2-1/(2x^2))/(sqrt(pi)*x)
elseif abs(ax) > 3 && abs(bx) > 3 ...
&& sign(ax)*sign(bx) == -1 % erfs saturates at +1 and -1
mu = z0 + (-2*exp(-ax^2)+2*exp(-bx^2))/...
(sqrt(2*pi*pz)*(...
-sign(ax)*erfc(abs(ax))+...
-sign(bx)*erfc(abs(bx))));
else
mu = z0 + (-2*exp(-ax^2)+2*exp(-bx^2))/...
(sqrt(2*pi*pz)*(erf(ax)+erf(bx)));
end
end
end

w = w + mu*uv*e;