算法|图论 6 并查集

并查集基本模板：

int n = 10;
vector UFSets(n,0);//若将初值全设置为-1，那就不用再有初始化操作了。

//初始化
void Initial(vector<int> S[]){
    for(int i=0;i<n;i++){
        S[i] = -1;
    }
}

//查操作
int Find(vector<int> &S,int x){
    int root = x;
    while(s[root] >= 0) root = S[root]//先找到x的根
    while(x != root){//压缩路径
        int t = S[x];//首先找到x的父亲，防止一会丢失找不到了
        S[x] = root;//将x挂到根节点下
        x = t;//再让x变为其父亲，将路径上所有节点都直接挂到根上
    }
    return root;
}

void Union(vector<int> &S,int x,int y){
    int Root1 = Find(S,x);
    int Root2 = Find(S,y);
    if(Root1 == Root2) return;
    if(S[Root2] > S[Root1]){//Root2节点数少，应该将其挂在Root1上面
        S[Root1] += S[Root2];//将两个集的节点数加起来
        S[Root2] = Root1;//小树挂到大树上去
    }else{
        S[Root2] += S[Root1];
        S[Root1] = Root2;
    }
    return ;
}

LeetCode 1971- 寻找图中是否存在路径

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目描述：有一个具有 n 个顶点的双向图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

解题思路

使用并查集，初始我们将所有边都每个edges都Union，这样就将连在一起的边都接在同一个树下了，然后再find找到看是否为同一个根，是则返回true，否则返回false。

class Solution {
public:
//初始化
void Initial(vector<int> &S){
    for(int i=0;i<S.size();i++){
        S[i] = -1;
    }
}

//查操作
int Find(vector<int> &S,int x){
    int root = x;
    while(S[root] >= 0) root = S[root];//先找到x的根
    while(x != root){//压缩路径
        int t = S[x];//首先找到x的父亲，防止一会丢失找不到了
        S[x] = root;//将x挂到根节点下
        x = t;//再让x变为其父亲，将路径上所有节点都直接挂到根上
    }
    return root;
}

void Union(vector<int> &S,int x,int y){
    int Root1 = Find(S,x);
    int Root2 = Find(S,y);
    if(Root1 == Root2) return;
    if(S[Root2] > S[Root1]){//Root2节点数少，应该将其挂在Root1上面
        S[Root1] += S[Root2];//将两个集的节点数加起来
        S[Root2] = Root1;//小树挂到大树上去
    }else{
        S[Root2] += S[Root1];
        S[Root1] = Root2;
    }
    return ;
}
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<int> UFSets(n,-1);//若将初值全设置为-1，那就不用再有初始化操作了。
        for(int i=0;i<edges.size();i++){
            Union(UFSets,edges[i][0],edges[i][1]);
        }
        if(Find(UFSets,source) == Find(UFSets,destination)) return true;
        return false;
    }
};

总结：并查集的Union就可以用来初始化边与边之间的联系，不需要你手动去给每个根和节点赋值。

LeetCode 684- 冗余连接

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目描述：树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

解题思路

和上一题的区别就是我们这次需要删除一条冗余的边。这次我们不直接union节点，我们先判断，若这两条边没有连在一起，也就是根不同，我们再union。若这两条边已经连在一起，就说明现在这条边是冗余的了，我们就直接返回这条边即可。

class Solution {
public:
    int Find(vector<int> &S,int x){
        int root = x;
        while(S[root] >= 0) root = S[root];
        while(x != root){
            int t = S[x];
            S[x] = root;
            x = t;
        }
        return root; 
    }
    void Union(vector<int> &S,int x,int y){
        int root1 = Find(S,x);
        int root2 = Find(S,y);
        if(root1 == root2) return;
        if(S[root1] > S[root2]){//root2根下树叶多一些
            S[root2] += S[root1];
            S[root1] = root2;
        }else{
            S[root1] += S[root2];
            S[root2] = root1;
        }
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> UFSets(1001,-1);
        for(int i=0;i<edges.size();i++){
            int node1 = edges[i][0];
            int node2 = edges[i][1];
            if(Find(UFSets,node1) != Find(UFSets,node2)) Union(UFSets,node1,node2);
            else return edges[i];
        }
        return vector<int>{};
    }
};

总结：并查集的Union就可以用来建立边与边之间的联系。

LeetCode 685.冗余连接II

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目描述：在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。每个元素是一对 [ui, vi]，用以表示有向图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

解题思路

本题明确告诉我们多了一条边，需要我们删除，然后让图变成树，有三种情况。

情况一（有一个节点入度为2）：

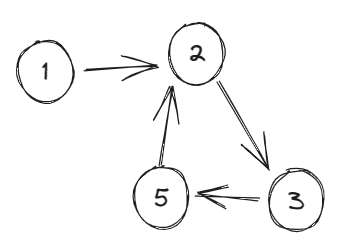
情况二：

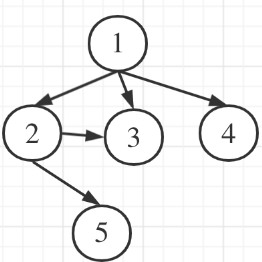
没有节点入度为2时

情况三（成环）：

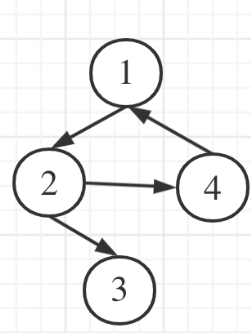
和上一题的区别就是我们这次需要删除一条边，并且这个图是有向图，难度就上来了。这题的基本思路就是：

首先写出并查集
第二再根据每个edge计算每个节点的入度，（为什么不看出度，因为每个节点都可能有多个出度，只有入度才是别的点到它，说明有多条路径可以走到当前节点，所以看入度）根据题目的描述，只有一个节点的入度会大于1，也就是2。并且只会有两条边导致入度为2，所以我们将这两条边加入待删队列中。然后再判断删除这两条边，图中是否能变成一棵树，如果可以则返回当前这条边，否则返回另一条边。因为这两条边一定有一条是构成环的边，删除就能变成树。
第三，若没有入度为2的边，那一定是情况三，构成环了。我们直接删除构成环的那条边就可以。


class Solution {
private:
    static const int N = 1010; // 如题：二维数组大小的在3到1000范围内
    int father[N];
    int n; // 边的数量
    // 并查集初始化
    void init() {
        for (int i = 1; i <= n; ++i) {
            father[i] = i;
        }
    }
    // 并查集里寻根的过程
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }
    // 将v->u 这条边加入并查集
    void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return ;
        father[v] = u;
    }
    // 判断 u 和 v是否找到同一个根
    bool same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }
    // 在有向图里找到删除的那条边，使其变成树
    vector<int> getRemoveEdge(const vector<vector<int>>& edges) {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) { // 遍历所有的边
            if (same(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边
                return edges[i];
            }
            join(edges[i][0], edges[i][1]);
        }
        return {};
    }

    // 删一条边之后判断是不是树
    bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) {
            if (i == deleteEdge) continue;
            if (same(edges[i][0], edges[i][1])) { // 构成有向环了，一定不是树
                return false;
            }
            join(edges[i][0], edges[i][1]);
        }
        return true;
    }
public:

    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int inDegree[N] = {0}; // 记录节点入度
        n = edges.size(); // 边的数量
        for (int i = 0; i < n; i++) {
            inDegree[edges[i][1]]++; // 统计入度
        }
        vector<int> vec; // 记录入度为2的边（如果有的话就两条边）
        // 找入度为2的节点所对应的边，注意要倒叙，因为优先返回最后出现在二维数组中的答案
        for (int i = n - 1; i >= 0; i--) {
            if (inDegree[edges[i][1]] == 2) {
                vec.push_back(i);
            }
        }
        // 处理图中情况1 和 情况2
        // 如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树
        if (vec.size() > 0) {
            if (isTreeAfterRemoveEdge(edges, vec[0])) {
                return edges[vec[0]];
            } else {
                return edges[vec[1]];
            }
        }
        // 处理图中情况3
        // 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
        return getRemoveEdge(edges);

    }
};

总结：并查集的Union就可以用来建立边与边之间的联系。