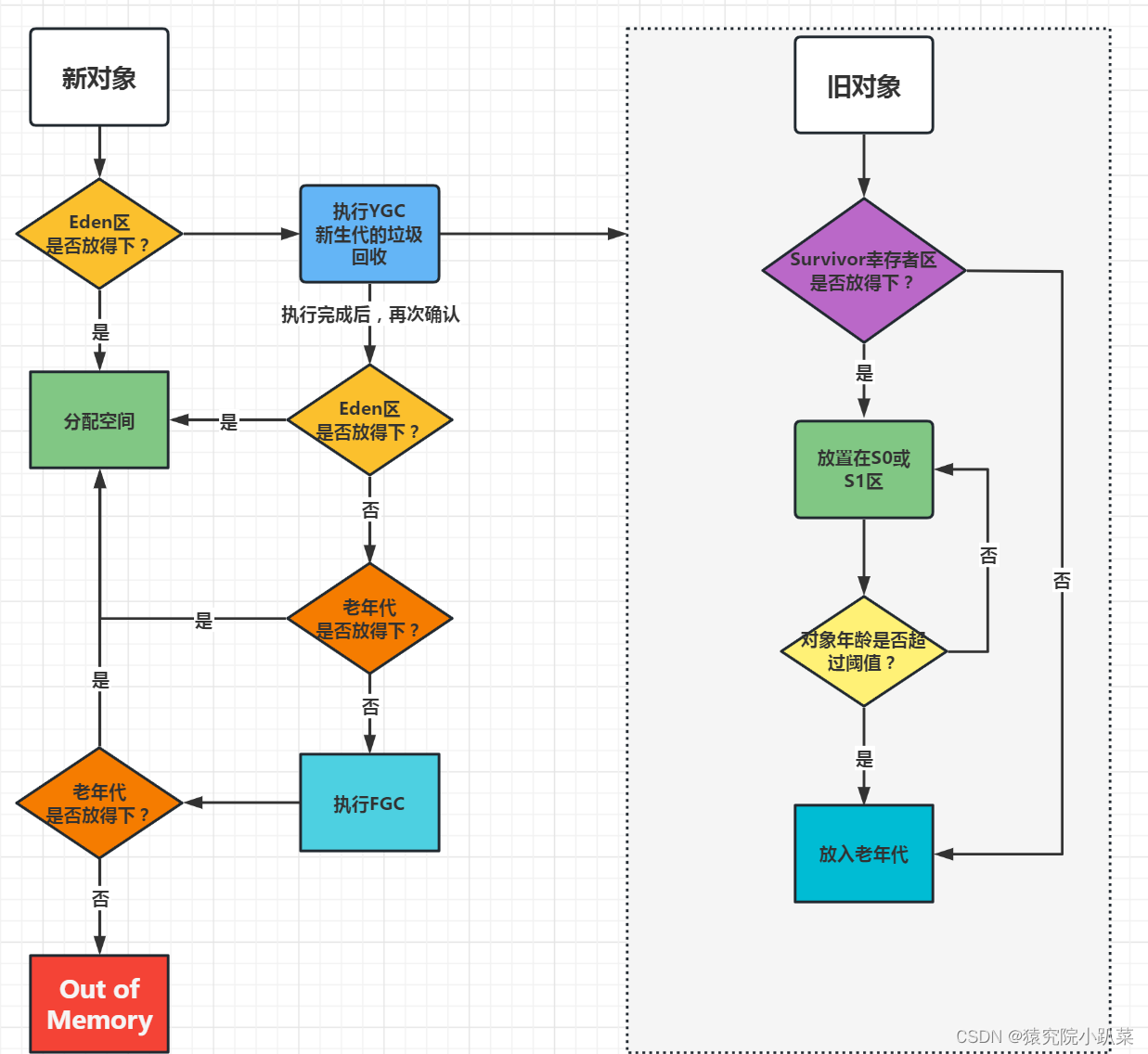
适用对象：事物发展具有明显阶段性

---

一、差分方程介绍

差分方程是一种描述离散系统演化的数学工具。与微分方程不同，差分方程使用差分代替微分来描述变量之间的关系。

差分方程通常由递归关系定义。假设有一个序列 {y₀, y₁, y₂, y₃, ...}，其中每个元素 yₙ 的值由它之前的元素决定。差分方程可表示为 yₙ = f(yₙ₋₁, yₙ₋₂, ...)，其中 f 是一个给定的函数。

举个例子，考虑斐波那契数列，其中每个元素是前两个元素的和。我们可以用差分方程来表示它：yₙ = yₙ₋₁ + yₙ₋₂，其中 y₀ = 0，y₁ = 1。根据这个方程，我们可以计算出数列的每个元素。

差分方程在许多领域中有广泛的应用，例如计算机科学、物理学、经济学等。通过建立差分方程模型，我们可以研究系统的演化和行为，预测未来的状态，优化决策等。

二、差分方程解基本知识

1、常系数线性齐次差分方程

【1】 其中k为差分方程的阶数；称为差分方程的系数，且

又称 【2】为差分方程【1】的特征方程，其根称为特征根。

2、常系数线性差齐次分方程的解的构成

2.1 特征根为单根情况

若【2】有k个单根则差分方程【1】的通解为【3】

 其中c1,c2,…,ck为任意常数，由初值条件

 【4】

 确定一个特解。

2.2 特征根为重根情况

若差分方程【2】有m个相异的特征根 重数分别为L1,L2,…,Lm,且则差分方程【1】的通解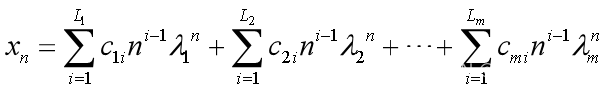【5】

 同样，由初值条件【4】可以确定一个特解。

2.3 特征根为复根情况 

若特征方程【2】有一对共轭复根 和相异的k-2个单根则差分方程【1】的通解为【6】

 其中同样在初值条件【4】给定时确定一个特解

3、常系数线性非齐次差分方程的解的构成

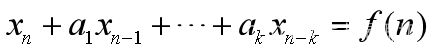 【7】

称为常系数非齐次差分方程，其中ak≠0.其通解为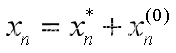【8】

其中xn*为【1】的通解，xn(0)为【7】的特解。 

三、差分方程的平衡点及其稳定性

 当差分方程的求解困难时，实际问题往往不用求出差分方程的一般解，只需要研究它的平衡点及其稳定性即可（即差分方程所代表的系统是趋于稳定的，不会突变或发散）。

1、一阶线性常系数差分方程

【9】

其中a,b为常数。它的平衡点由代数方程x+ax=b求解得到，不妨记为x*,若满足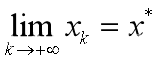

则称x*是稳定的，否则是不稳定的 。一般地，【9】稳定的充分必要条件为|a|<1。

2、一阶常系数差分方程组 

 【10】

其中，x(k)为n维向量，A为n×n的常数矩阵。 

【10】的平衡点x*是稳定的充分必要条件是A的所有特征根都有 （即特征根都位于单位圆内）

3、二阶线性常系数差分方程 

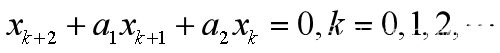 【11】

其中a1,a2为常数。其平衡点x*=0的充分必要条件是特征方程的根在单位圆内。 

4、一阶非线性差分方程 

 【12】

 其中f为已知函数，其平衡点定义为x=f(x)的解x*。将f(xk)在x*处作一阶泰勒展开有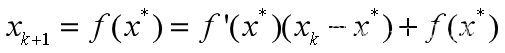【13】

x*也是一阶线性差分方程【13】的平衡点，故x*稳定的充分必要条件是