目录

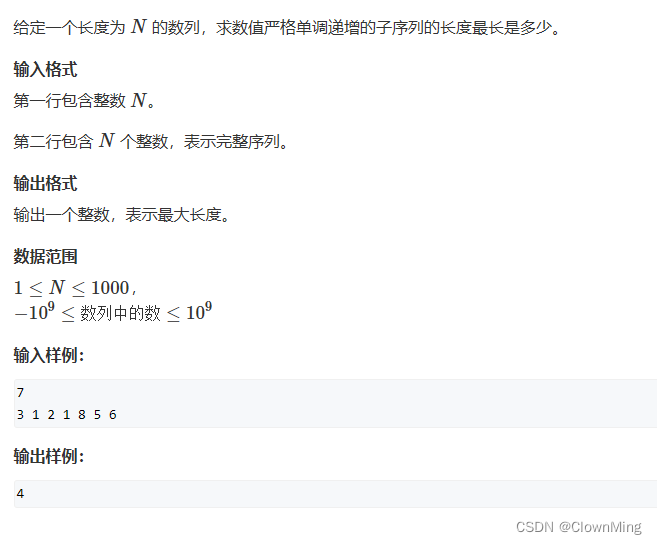
题目：

示例：

分析：

代码：

---

题目：

示例：

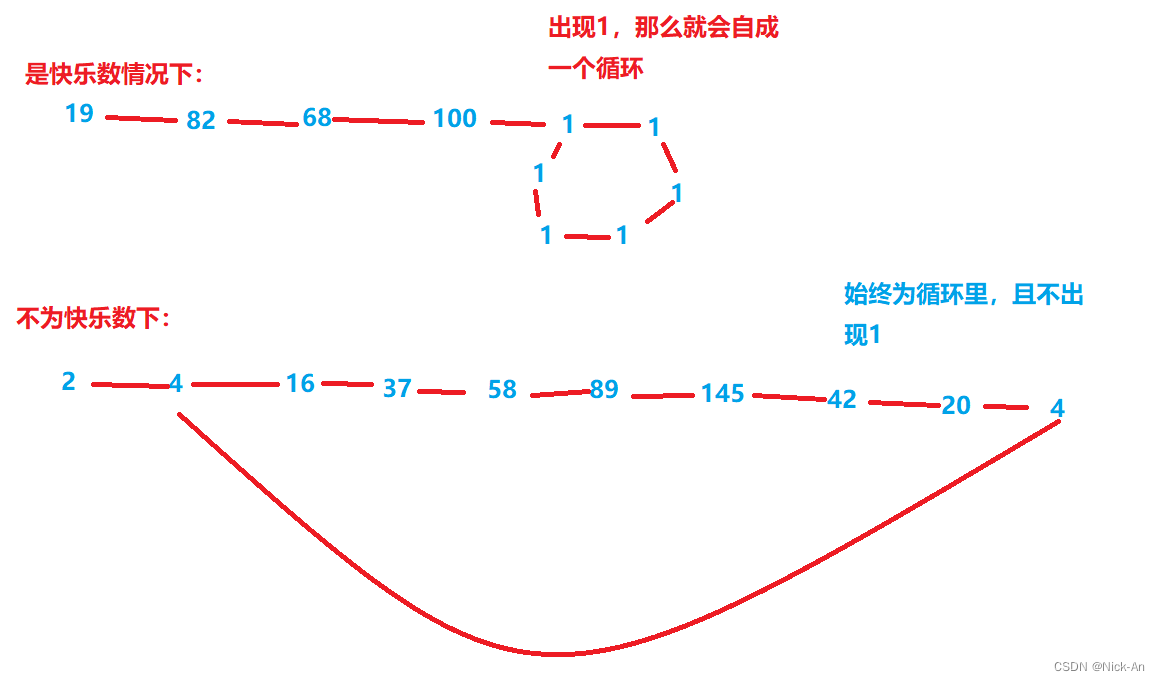
分析：

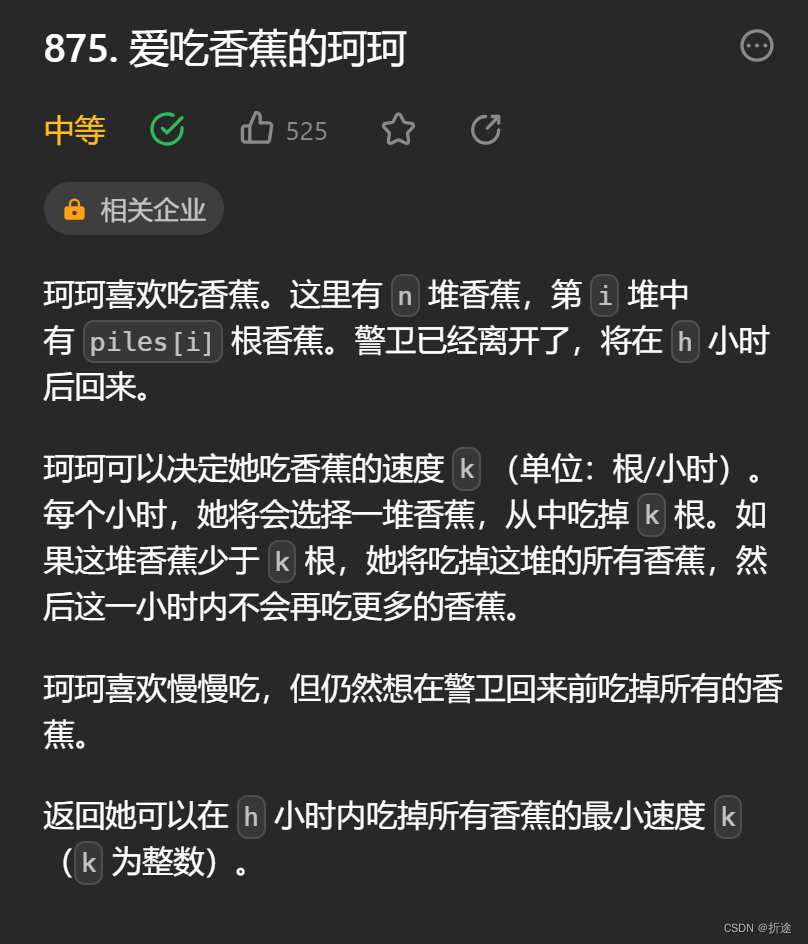
这道题挺炸裂的，题目给我们一个数组，数组里的每个元素表示每个仓库里的香蕉数量。

珂珂可以自己控制自己吃香蕉的速度，也就是每小时可以吃几根香蕉，不过同一个小时只会待在同一个仓库里，也就是所就算吃完了一个仓库的香蕉，并且一小时里还有剩余时间，它也不会跑去其他仓库吃。

问我们在h小时内吃完所有仓库的所需最小的速度是多少，因为珂珂这个b想要慢慢地偷吃。

首先题目给出条件：

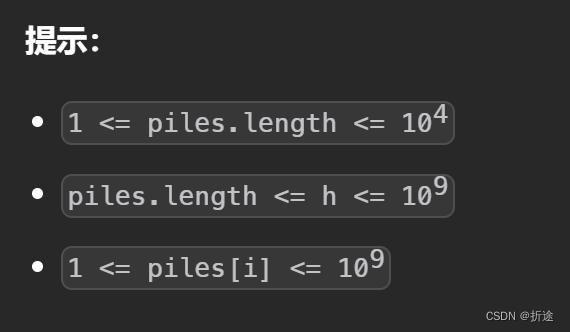
 h是大于仓库数量的，所以我们是一定的得出答案的。

如果把速度定成所有仓库里最多的香蕉数，那么吃完吃需要仓库数量的时间，也是至少要花的时间，因为你速度再提高也不会减少花费的时间。

而速度最低定成1，那么吃完仓库数量的时间就是所有仓库里香蕉的数量总和。

我们就把速度的范围定下来了，就是 [ 1 , 仓库里最多的香蕉数 ] ，确定范围之后，我们可以使用二分查找法来进一步缩小范围，最终确定答案。

我们每次取范围的中间数当作速度，看看按照这个速度吃完的时间有没有超过h，如果没有超过，那么就说明我们还有可能可以再慢一些，那么我们收缩右范围来使得范围的中位数变小。如果超过了h，那就说明我们的速度偏慢了，得提高速度，那么就要收缩左范围来使得范围的中位数变大。

最终我们就可以把范围缩小到答案。

代码：

class Solution {
public:
    int eat(const vector<int>& piles,int time){ //如果以time的速度吃,需要多久
        int ans=0;
        for(int p:piles){
            //如果剩余数量不是time的整数倍,那么需要额外+1
            if(p%time!=0)   ans++;
            ans+=p/time;
        }
        return ans;
    }
    int minEatingSpeed(vector<int>& piles, int h) {
        int l=1;int r=piles[0]; //左闭右闭
        for(int p:piles) r=max(r,p);
        int time;
        int res=r;
        while(l<r){
            int temp=l+(r-l)/2;
            time=eat(piles,temp);
            if(time<=h){    //如果当前速度满足条件,那么缩小右边界看看能不能用更小的速度.
                res=temp;
                r=temp;
            }else{  //如果不满足条件,那么缩小左边界,提升速度.
                l=temp+1;
            }
        }
        return res;
    }
};