在一个 8x8 的棋盘上,放置着若干「黑皇后」和一个「白国王」。
给定一个由整数坐标组成的数组 queens ,表示黑皇后的位置;以及一对坐标 king ,表示白国王的位置,返回所有可以攻击国王的皇后的坐标(任意顺序)。
示例 1:
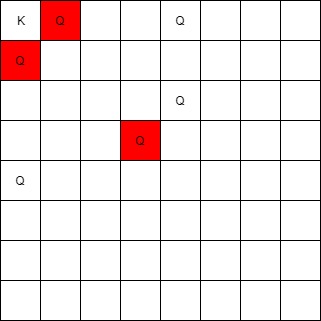
输入:queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] 输出:[[0,1],[1,0],[3,3]] 解释: [0,1] 的皇后可以攻击到国王,因为他们在同一行上。 [1,0] 的皇后可以攻击到国王,因为他们在同一列上。 [3,3] 的皇后可以攻击到国王,因为他们在同一条对角线上。 [0,4] 的皇后无法攻击到国王,因为她被位于 [0,1] 的皇后挡住了。 [4,0] 的皇后无法攻击到国王,因为她被位于 [1,0] 的皇后挡住了。 [2,4] 的皇后无法攻击到国王,因为她和国王不在同一行/列/对角线上。
示例 2:
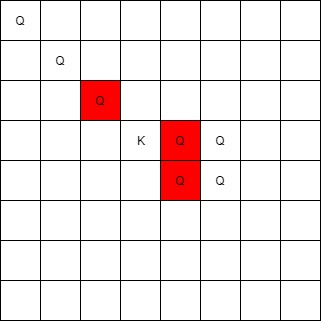
输入:queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] 输出:[[2,2],[3,4],[4,4]]
示例 3:
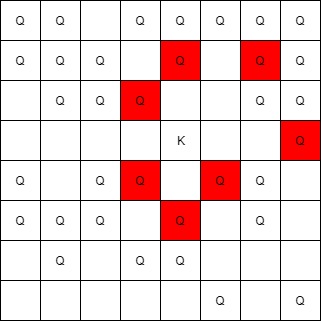
输入:queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4] 输出:[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
提示:
1 <= queens.length <= 63queens[i].length == 20 <= queens[i][j] < 8king.length == 20 <= king[0], king[1] < 8- 一个棋盘格上最多只能放置一枚棋子。
题目链接
核心做法:以国王为中心,分别向八个方向探索皇后的存在,在某个方向碰到皇后之后就换下一个方向找皇后(在一个方向找皇后的时候要注意不要越界),然后将找到的皇后的坐标存储到一个二维数组里面
int kx = king[0];
int ky = king[1];
int n = 8;
int arr[8][8] = {0}; // 记录皇后的位置
for (int i = 0; i < queensSize; i++) {
arr[queens[i][0]][queens[i][1]] = 1; // 标记
}
int rx = 0; // 返回的二维数组的下标创建一个二维数组用于标记皇后的位置,皇后在的位置值就为1,这个二维数组后续用于在一个方向上找皇后
// 创建一个动态分配的二维数组来存储结果
int** result = (int**)malloc(queensSize * sizeof(int*));
for (int i = 0; i < queensSize; i++) {
result[i] = (int*)malloc(2 * sizeof(int));
}用于存储能够打到国王的皇后
// 横坐标相等(左边)
for (int j = ky - 1; j >= 0; j--) {
if (arr[kx][j] == 1) {
result[rx][0] = kx;
result[rx][1] = j;
rx++;
break;
}
}
// 横坐标相等(右边)
for (int j = ky + 1; j < 8; j++) {
if (arr[kx][j] == 1) {
result[rx][0] = kx;
result[rx][1] = j;
rx++;
break;
}
}
// 纵坐标相等(上面)
for (int i = kx - 1; i >= 0; i--) {
if (arr[i][ky] == 1) {
result[rx][0] = i;
result[rx][1] = ky;
rx++;
break;
}
}
// 纵坐标相同(下面)
for (int i = kx + 1; i < 8; i++) {
if (arr[i][ky] == 1) {
result[rx][0] = i;
result[rx][1] = ky;
rx++;
break;
}
}
在相同的横纵方向上找离国王最近的皇后
// 左上方
int num1 = 1;
while(kx-num1>=0 && ky-num1>=0){
if(arr[kx-num1][ky-num1]==1){
result[rx][0] = kx-num1;
result[rx][1] = ky-num1;
rx++;
break;
}
num1++;
}
// 右下方
int num = 1;
while (kx + num < 8 && ky + num < 8) {
if (arr[kx + num][ky + num] == 1) {
result[rx][0] = kx + num;
result[rx][1] = ky + num;
rx++;
break;
}
num++;
}
// 右上方
int num2 = 1;
while (kx - num2 >= 0 && ky + num2 < 8) {
if (arr[kx - num2][ky + num2] == 1) {
result[rx][0] = kx - num2;
result[rx][1] = ky + num2;
rx++;
break;
}
num2++;
}
// 左下方
int num3 = 1;
while (kx + num3 < 8 && ky - num3 >= 0) {
if (arr[kx + num3][ky - num3] == 1) {
result[rx][0] = kx + num3;
result[rx][1] = ky - num3;
rx++;
break;
}
num3++;
}
再找斜线上的皇后的时候要注意不要越界,所以我在循环的判断语句中保证向斜对角线探索的坐标不会超过界限,然后在这个方向上找皇后的位置,如果找到的就把坐标存到之前动态分配的二维数组里面去,否则继续往下找,直到边界
// 设置返回的数组大小
*returnSize = rx;
// 分配列大小数组的内存
*returnColumnSizes = (int*)malloc(rx * sizeof(int));
for (int i = 0; i < rx; i++) {
(*returnColumnSizes)[i] = 2; // 每行有两列
}
return result; // 返回结果数组将得到的数值赋给相应的变量
完整代码
int** queensAttacktheKing(int** queens, int queensSize, int* queensColSize, int* king, int kingSize, int* returnSize, int** returnColumnSizes) {
int kx = king[0];
int ky = king[1];
int n = 8;
int arr[8][8] = {0}; // 记录皇后的位置
for (int i = 0; i < queensSize; i++) {
arr[queens[i][0]][queens[i][1]] = 1; // 标记
}
int rx = 0; // 返回的二维数组的下标
// 创建一个动态分配的二维数组来存储结果
int** result = (int**)malloc(queensSize * sizeof(int*));
for (int i = 0; i < queensSize; i++) {
result[i] = (int*)malloc(2 * sizeof(int));
}
// 横坐标相等(左边)
for (int j = ky - 1; j >= 0; j--) {
if (arr[kx][j] == 1) {
result[rx][0] = kx;
result[rx][1] = j;
rx++;
break;
}
}
// 横坐标相等(右边)
for (int j = ky + 1; j < 8; j++) {
if (arr[kx][j] == 1) {
result[rx][0] = kx;
result[rx][1] = j;
rx++;
break;
}
}
// 纵坐标相等(上面)
for (int i = kx - 1; i >= 0; i--) {
if (arr[i][ky] == 1) {
result[rx][0] = i;
result[rx][1] = ky;
rx++;
break;
}
}
// 纵坐标相同(下面)
for (int i = kx + 1; i < 8; i++) {
if (arr[i][ky] == 1) {
result[rx][0] = i;
result[rx][1] = ky;
rx++;
break;
}
}
// 左上方
int num1 = 1;
while(kx-num1>=0 && ky-num1>=0){
if(arr[kx-num1][ky-num1]==1){
result[rx][0] = kx-num1;
result[rx][1] = ky-num1;
rx++;
break;
}
num1++;
}
// 右下方
int num = 1;
while (kx + num < 8 && ky + num < 8) {
if (arr[kx + num][ky + num] == 1) {
result[rx][0] = kx + num;
result[rx][1] = ky + num;
rx++;
break;
}
num++;
}
// 右上方
int num2 = 1;
while (kx - num2 >= 0 && ky + num2 < 8) {
if (arr[kx - num2][ky + num2] == 1) {
result[rx][0] = kx - num2;
result[rx][1] = ky + num2;
rx++;
break;
}
num2++;
}
// 左下方
int num3 = 1;
while (kx + num3 < 8 && ky - num3 >= 0) {
if (arr[kx + num3][ky - num3] == 1) {
result[rx][0] = kx + num3;
result[rx][1] = ky - num3;
rx++;
break;
}
num3++;
}
// 设置返回的数组大小
*returnSize = rx;
// 分配列大小数组的内存
*returnColumnSizes = (int*)malloc(rx * sizeof(int));
for (int i = 0; i < rx; i++) {
(*returnColumnSizes)[i] = 2; // 每行有两列
}
return result; // 返回结果数组
}