无约束优化：线搜索最速下降

无约束优化问题

线搜索最速下降

对于光滑函数$f(x)$，沿着函数负梯度方向下降速度最快。对于线搜索最速下降方法而言，核心问题是如何选择搜索步长$\tau$，一般有以下四种方法：

• 固定步长：$\tau =c$。如下图所示，若常数取太大，则搜索振荡厉害且对于非凸函数有可能发散；若太小，则收敛速度慢；
• 渐消步长：$\tau =c/k$。适用性强，对于非光滑函数、梯度存在噪声（$▽f(x{)}^{\prime }=▽f(x)+\epsilon$ ，随机噪声）适用，稳健性强但收敛速度慢，适用于条件差但对收敛速度要求不高的场景；
• 精确线搜索：$\tau =\arg {\min }_{\alpha }f\left(x^k+\alpha d\right)$，实际应用较少，下面详述；
• 非精确线搜索：$\tau \in \left\{\alpha \mid f\left(x^k\right)-f\left(x^k+\alpha d\right)\ge -c\cdot \alpha d^{\mathrm{T}}\nabla f\left(x^k\right)\right\}$，重要，下面详述。

精确线搜索

此时我们构造了一个辅助函数$\varphi (\alpha )=f\left(x^k+\alpha d^k\right)$，$\alpha$是该辅助函数的自变量，该函数的几何含义非常直观：它是目标函数$f(x)$在射线$\left\{x^k+\alpha d^k:\alpha >0\right\}$上的限制。线搜索的目标就是选取合适的${\alpha }_k$使得$\varphi \left({\alpha }_k\right)$尽可能小，自然而言引入一个子优化问题：
$${\alpha }_k=\underset{\alpha >0}{\mathrm{argmin}}\varphi (\alpha )$$
这个子优化算法就是精确线搜索，目的是找到精确的最佳步长${\alpha }_k$。但在原本的最速下降优化问题中再引入一个子优化问题，这本身就带来比较大的计算量，因此精确线搜索在实际应用中较少使用。由此，引出非精确线搜索算法，即把条件放宽，不要求得到精确的最佳步长${\alpha }_k$，而是仅仅要求$\varphi (\alpha )$满足某些不等式要求。

非精确线搜索

Armijo准则

设$d^k$是点$x^k$处的下降方向，若$f\left(x^k+\alpha d^k\right)⩽f\left(x^k\right)+c_1\alpha \nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k$，则称步长$\alpha$满足Armijo准则，其中$c_1\in (0,1)$是一个常数。一般$d^k$为负梯度方向，则$c_1\alpha \nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k<0$，若满足Armijo准则，则严格满足$f\left(x^k+\alpha d^k\right)<f\left(x^k\right)$，因此又称该准则为充分下降条件，可保证每一步迭代充分下降。

该准则有非常直观的几何含义，如上图所示。在实际应用中，参数$c_1$通常选为一个很小的正数，例如$c_1=10^{-3}$，这使得Armijo准则非常容易满足。但仅仅使用该准则无法保证迭代的收敛性，因为取$\alpha =0$也是满足准则中的条件，而这意味着迭代序列中的点固定不变，这样重复收敛就没有意义，因此Armijo准则一般搭配其他准则来使用。基于Armijo准则的最速下降算法步骤如下：

上述算法不会无限进行下去，因为沿着梯度负方向，当$\alpha$充分小时，该准则总是成立的。为了避免步长过小，在实际应用中一般会给$\alpha$设置一个下界，这就是Goldstein准则。

Goldstein准则

Armijo-Goldstein准则，简称Goldstein准则，简单来说就是同时给$\alpha$设置上下界，定义如下：

设$d^k$是点$x^k$处的下降方向，若
$$\begin{array}{rl}& f\left(x^k+\alpha d^k\right)⩽f\left(x^k\right)+c\alpha \nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k,\\ & f\left(x^k+\alpha d^k\right)⩾f\left(x^k\right)+(1-c)\alpha \nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k\end{array}$$
则称步长$\alpha$满足Goldstein准则，其中$c\in (0,0.5)$.

该准则的几何意义同样非常直观，如上图所示，在区间$[{\alpha }_1,{\alpha }_2]$中的点均满足Goldstein准则。但需要注意的是，该准则可能避开最优的函数值，$\varphi (\alpha )$的最小值点并不在区间$[{\alpha }_1,{\alpha }_2]$内。为此，我们引入Armijo-Wolfe准则。

Wolfe准则

Armijo-Wolfe准则，简称Wolfe准则，定义如下：

设$d^k$是点$x^k$处的下降方向，若
$$\begin{array}{rl}& f\left(x^k+\alpha d^k\right)⩽f\left(x^k\right)+c_1\alpha \nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k\\ & \nabla f{\left(x^k+\alpha d^k\right)}^{\mathrm{T}}{d}^k⩾c_2\nabla f{\left(x^k\right)}^{\mathrm{T}}{d}^k\end{array}$$
则称步长$\alpha$满足Wolfe准则，其中$c_1,c_2\in (0,1)$为给定常数且$c_1<c_2$.

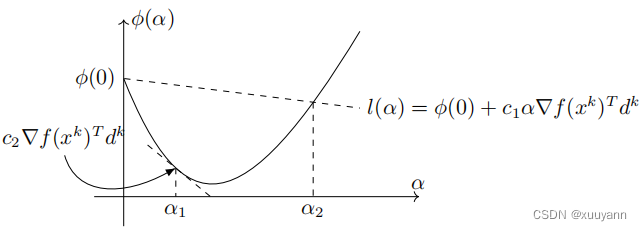
由该准则的定义可以看出，仍然使用第一个条件即Armijo准则确定步长上界，在第二个条件中$\nabla f{\left(x^k+\alpha d^k\right)}^{\mathrm{T}}{d}^k$是$\varphi (\alpha )$的导数，也就是要求$\varphi (\alpha )$在点$\alpha$处切线的斜率不能小于${\varphi }^{\prime }(0)$的$c_2$倍。如下图所示，在区间$[{\alpha }_1,{\alpha }_2]$中的点均满足Wolfe准则，${\alpha }_k=\underset{\alpha >0}{\mathrm{argmin}}\varphi (\alpha )$子优化问题的最优解处（$\varphi (\alpha )$的极小值点）有${\varphi }^{\prime }\left({\alpha }^{\ast }\right)=\nabla f{\left(x^k+{\alpha }^{\ast }{d}^k\right)}^{\mathrm{T}}{d}^k=0$，永远满足Wolfe准则的第二个条件。因此，该准则在绝大多数情况下包含线搜索子问题的精确解，在实际应用中，参数$c_2=0.9$.

---

参考文献

机器人中的数值优化

最优化：建模、算法与理论/最优化计算方法